2)Параллелепипед называ­ется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

Форму прямоугольного параллелепипеда имеют коробки, ящики, комнаты и т. д.

1°. В прямоугольном параллелепипеде все шесть граней — прямоугольники.

Полуплоскости, в которых расположены смежные грани парал­лелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда.

2°. Все двугранные углы прямоугольного параллелепипеда — прямые.

Перейдем теперь к рассмотрению одного из самых замечатель­ных свойств прямоугольного параллелепипеда.

Длины трех ребер, имеющих общую вершину, назовем из­мерениями прямоугольного параллелепипеда.

В обыденной практике, измерения называют шириной, длиной, высотой.

Прежде чем сформулировать свойство параллелепипеда, связанное с его измерениями, вспомним, что в прямоуголь­нике квадрат диагонали равен сумме квадратов смежных сторон.

Длины смежных сторон можно назвать измерениями пря­моугольника и поэтому можно сказать, что квадрат диагонали прямоугольника равен сумме квадратов двух его измерений. Оказывается, аналогичным свойством обладает и прямоугольный параллелепипед.

Т еорема

Квадрат диагонали прямоугольного параллеле­пипеда равен сумме квадратов трех его измерений.

Доказательство

Обратимся к рисунку, на котором изображен параллелепипед АВСDА₁В₁С₁D₁, и докажем, что

.

Так как ребро СС₁ перпендикулярно к основанию АВСD, то угол АСС₁ прямой. Из прямоугольного треугольника АСС₁ по теореме Пифагора получаем

АС₁²= АС² + СС₁²

Но АС — диагональ прямоугольника АВСD, поэтому АС² =АВ²+АD². Кроме того, СС₁ = АА₁. Следовательно

АС₁² = АВ² + АD² + АА₁².

Теорема доказана.

Следствие.

Диагонали прямоугольного параллелепипеда равны.

Прямоугольный параллелепипед, у которого все три измере­ния равны, называется кубом. Все грани куба — равные друг другу квадраты.

Теорема доказана.

Билет№8

1)Определение

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пере­секаются.

Лемма

Е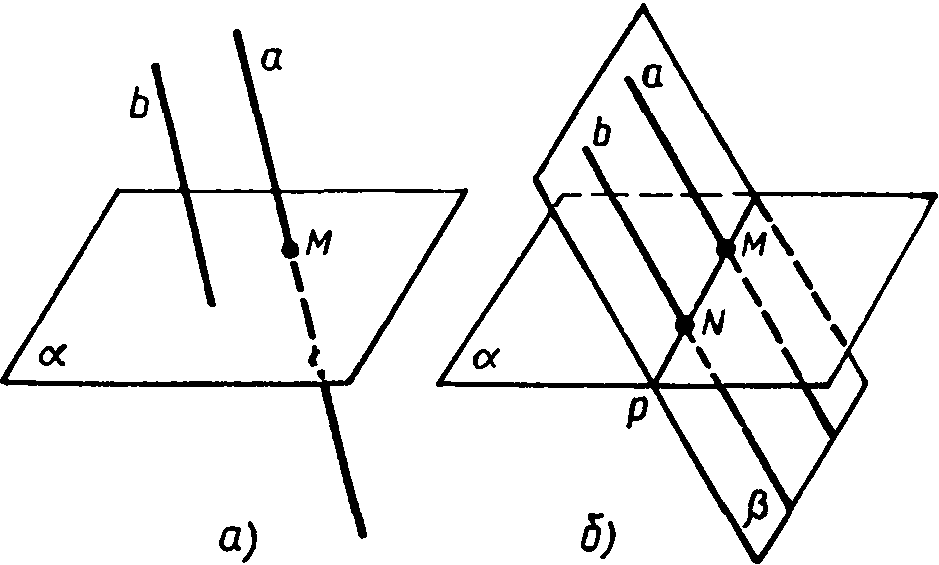 сли одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

Рассмотрим параллельные прямые а и b, одна из которых — прямая а — пересекает плоскость ά в точ­ке М. Докажем, что прямая b также пересекает плоскость ά,

т. е. имеет с ней только одну общую точку.

Обозначим буквой β плоскость, в которой лежат параллель­ные прямые а и b. Так как две различные плоскости ά и β имеют общую точку М, то по аксиоме А₃ они пересекаются по некоторой прямой р. Эта прямая лежит в плоскости β и пере­секает прямую а (в точке М), поэтому она пересекает парал­лельную ей прямую b в некоторой точке N. Прямая р лежит также в плоскости ά, поэтому N — точка плоскости ά. Следовательно, N — общая точка прямой b и плоскости ά.

Докажем теперь, что прямая b не имеет других общих точек с плоскостью ά, кроме точки N. Это и будет означать, что пря­мая b пересекает плоскость ά. Действительно, если бы прямая b имела еще одну точку с плоскостью ά, то она целиком лежала бы в плоскости ά и, значит, была бы общей прямой плоскос­тей ά и β, т. е. совпадала бы с прямой р. Но это невозможно, так как по условию а||b, а прямые а и р пересекаются.

Лемма до­казана.

2 )Из курса планиметрии известно, что если три прямые лежат в одной плос­кости и две из них параллельны треть­ей прямой, то эти две прямые парал­лельны. Докажем аналогичное утверж­дение для трех прямых в пространстве.

Теорема

Если две прямые па­раллельны третьей прямой, то они па­раллельны.

Доказательство

Пусть a||с и b||с. Докажем, что а||b. Для этого нужно доказать, что прямые а и b:

1) лежат в одной плоскости

2) не пересекаются.

1) Отметим какую-нибудь точку К на прямой b и обозначим буквой ά плоскость, проходящую через прямую а и точку К. Докажем, что прямая b лежит в этой плоскости. Дей­ствительно, если допустить, что прямая b пересекает плоскость ά, то по лемме о пересечении плоскости параллельными прямыми прямая с также пересекает плоскость ά. Но так как с||а, то и прямая а пересекает плоскость ά, что невозможно, ибо прямая а лежит в плоскости ά.

2) Прямые а и b не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые (а и b), параллельные прямой с, что невозможно.

Теорема доказана.