
- •Билет№1
- •1) Аксиомы стереометрии и следствия из них.
- •2) Теорема о боковой поверхности правильной пирамиды
- •Б илет №2
- •Билет№3
- •Билет№4
- •1) Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
- •2) Теорема
- •Билет№5
- •2) Понятие
- •Билет№6
- •2) Теорема
- •Билет№7
- •1) Понятие
- •2)Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
- •Билет№8
- •1)Определение
- •Б илет№9
- •1)Параллельные плоскости
- •Билет№10
- •1)Определение
- •2)Усеченная пирамида
- •Билет№11
- •2)Разложение вектора по трем некомпланарным векторам.
- •Билет№12
- •1) Углы с сонаправленными сторонами.
- •2)Теорема
- •Билет№13
- •2)Теорема
- •Б илет№14
- •1°. Противоположные грани параллелепипеда параллельны и равны.
- •2°. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- •2)Теорема
- •Билет№15
- •2)Теорема
2)Теорема
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Доказательство
Р ассмотрим прямую а, которая перпендикулярна к прямым p и q, лежащим в плоскости ά и пересекающимся в точке О. Докажем, что а ά. Для этого нужно доказать, что прямая а перпендикулярна к произвольной прямой m плоскости ά.
Рассмотрим сначала случай, когда прямая а проходит через точку О. Проведем через точку О прямую l, параллельную прямой m (если прямая m проходит через точку О, то в качестве l возьмем саму прямую m). Отметим на прямой а точки А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости а прямую, пересекающую прямые p, q и l соответственно в точках Р, Q и L. Будем считать для определенности, что точка Q лежит между точками Р и L.
Так как прямые p и q — серединные перпендикуляры к отрезку АВ, то АР = ВР и AQ = ВQ. Следовательно, АРQ= ВРQ по трем сторонам. Поэтому АРQ= ВРQ.
Сравним теперь треугольники АРL и ВРL. Они равны по двум сторонам и углу между ними (АР= ВР,PL—общая сторона, АРL— ВРL), поэтому АL — ВL. Но это означает, что треугольник АВL равнобедренный и его медиана LO является высотой, т. е. l а. Так как l||т и l а, то т а (по лемме о перпендикулярности двух параллельных прямых к третьей). Таким образом, прямая а перпендикулярна к любой прямой т плоскости ά, т. е. а ά.
Рассмотрим теперь случай, когда прямая а не проходит через точку О. Проведем через точку О прямую а1, параллельную прямой а. По упомянутой лемме а1 р и а1 q, поэтому по доказанному в первом случае а1 ά. Отсюда (по первой теореме п. 16) следует, что а ά.
Теорема доказана.
Билет№15
1)Пирамида. Рассмотрим
многоугольник А1А2...Аn
и точку Р,
не лежащую в плоскости
этого м ногоугольника.
Соединив точку Р отрезками
с вершинами многоугольника, получим п
треугольников:
ногоугольника.
Соединив точку Р отрезками
с вершинами многоугольника, получим п
треугольников:
РА1А2, РА2А3, ..., РАпА1. (1)
Многогранник, составленный из n-угольника А1А2...Аn и n треугольников (1), называется пирамидой. Многоугольник А1А2...Аn
называется основанием, а треугольники (1) — боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА1, РА2, ..., РАn — ее боковыми ребрами. Пирамиду с основанием А1А2...Аn и вершиной Р обозначают так: РА1А2...Аn— и называют n-угольной пирамидой. На рисунке изображены четырехугольная и шестиугольная пирамиды. Ясно, что треугольная пирамида — это тетраэдр.
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке отрезок РН — высота пирамиды.
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней. Очевидно,
Sполн=Sбок+Sосн (2)
Правильная пирамида.
Пирамида называется правильной,
если ее основание —
правильный м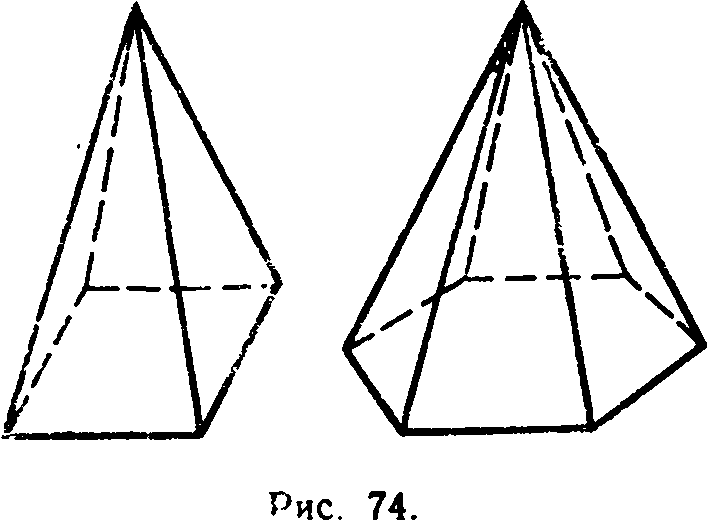 ногоугольник,
а отрезок, соединяющий вершину
пирамиды с центром основания, является
ее высотой.
ногоугольник,
а отрезок, соединяющий вершину
пирамиды с центром основания, является
ее высотой.
Докажем, что вес боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Рассмотрим правильную пирамиду РА1А2...Аn. Сначала докажем, что все боковые ребра этой пирамиды равны.
Л юбое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота РО пирамиды, а другим — радиус описанной около основания окружности (например, боковое ребро РА1 — гипотенуза треугольника ОРА1, в котором ОР = Н, ОА1=R). По теореме Пифагора любое боковое ребро равно , поэтому РА1=PA2 = ... = PAn.
Мы доказали, что боковые ребра правильной пирамиды PA1A2...An равны друг другу, поэтому боковые грани — равнобедренные треугольники.
Основания этих треугольников также равны друг другу, так как А1А1…Аn — правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников, что и тре0овалось доказать.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке отрезок РЕ — одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу.
Докажем теорему о площади боковой поверхности правильной пирамиды.
Теорема
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство
Боковые грани правильной пирамиды - равные равнобедренные треугольники, основания которых — стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произведений сторон основания на половину апофемы d. Вынося множитель
0,5d за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр.
Теорема доказана
