Билет№11

1)Компланарные векторы

Векторы называются компланар­ными, если при откладывании их от одной и той же точки они бу­дут лежать в одной плоскости. Другими словами, векторы назы­ваются компланарными, если имеются равные им векторы, лежа­щие в одной плоскости.

Ясно, что любые два вектора компланарны; три вектора, среди которых имеются два коллинеарных, также компланарны, а три произвольных вектора могут быть как комп­ланарными, так и не компланарными.

Признак компланарности трёх векторов

Если вектор с можно разложить по векторам а к b, т. е. пред­ставить в виде

с = х + у ,

где х и у — некоторые числа, то векторы а, b и с компланарны.

Доказательство

Будем считать, что векторы а и b не коллинеарны (если векторы a и b коллинеарны, то компланар­ность векторов очевидна). Отложим от произвольной

точки О векторы = и = . Векторы и лежат в плоскости ОАВ. Очевидно, в этой же плоскости лежат

векторы ₁=х * и ₁= у * , а следовательно, и их сум­ма— вектор = х * + у * , равный вектору с. Итак, векто­ры = , = и = лежат в одной плоскости, т. е. век­торы , и компланарны.

Теорема доказана.

Справедливо и обратное утверждение: если векторы , и компланарны, а векторы и не коллинеарны, то вектор мож­но разложить по векторам и , причем коэффициенты разложения определяются единственным образом.

2)Разложение вектора по трем некомпланарным векторам.

Если вектор представлен в виде

(2)

где х, у и z — некоторые числа, то говорят, что вектор разложен по векторам , и . Числа х, у, z называются коэффициентами разложения.

Докажем теорему о разложении вектора по трем некомпла­нарным векторам.

Теорема

Любой вектор можно разложить по трем данным не компланарным векторам, причем коэффициенты разложения определяются единственным образом.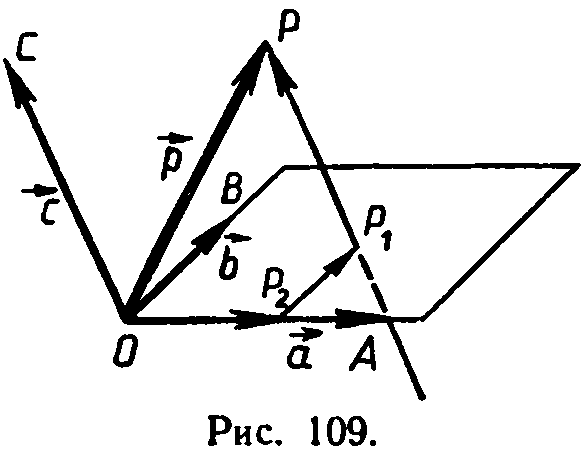

Доказательство

Пусть , , —данные некомпла­нарные векторы. Докажем сначала, что любой вектор можно разложить по трём векторам.

Отметим произвольную точку О и отложим от этой точки век­торы:

= , = , = , = .

Через точку Р проведем прямую, параллельную прямой ОС, и обозначим через Р₁ точку пересечения этой прямой с плос­костью АОВ (если Р ОС, то в качестве точки Р₁ возьмем точ­ку О). Затем через точку Р₁ проведем прямую, параллельную прямой ОВ, и обозначим через Р₂ точку пересечения этой прямой с прямой О А (если Р₁ ОВ, то в качестве точки Р₂ возьмем точ­ку О). По правилу многоугольника:

Векторы ₂ и , и , и коллинеарны, поэтому существуют числа х, у, z такие, что , . Подставив эти выражения в равенство, получим

Докажем теперь, что коэффициенты разложения в формуле опреде­ляются единственным образом. Допустим, что наряду с данным разложением имеется другое разложение вектора . Вычитая это равенство из ра­венства (2) и используя свойства действий над векторами, по­лучим

.

Это равенство выполняется только тогда, когда х-x₁=0, у-y₁=0, z-z₁=0. В самом деле, если предположить, например, что z-z₁ 0, то из этого равенства находим:

откуда следует, что векторы , , компланарны. Но это про­тиворечит условию теоремы. Значит, наше предположение невер­но, и x=x₁, у=у₁, z=z₁. Следовательно, коэффициенты разло­жения (2) определяются единственным образом.

Теорема до­казана.