Билет№1

1) Аксиомы стереометрии и следствия из них.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Некоторые следствия из аксиом:

Теорема

Через прямую и не лежащую на ней точку про­ходит плоскость, и притом только одна.

Доказательство.

Рассмотрим прямую а и не лежащую на ней точку М. Докажем, что через прямую а и точку М п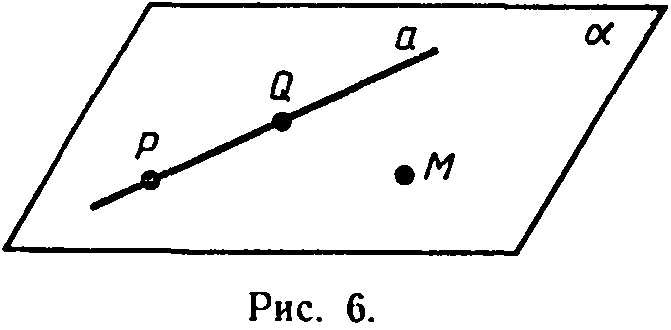 роходит плоскость. Отметим на прямой а две точки Р п Q. Точки М, Р и Q не лежат на одной прямой, поэтому согласно аксиоме А1 через эти точки проходит некоторая плоскость ά. Так как две точки прямой а (Р и Q) лежат в плоскости ά, то по аксиоме А₂ плоскость ά проходит через прямую а.

Единственность плоскости, проходящей через прямую а и точ­ку М, следует из того, что любая плоскость, проходящая через прямую а и точку М, проходит через точки М, Р и Q. Следова­тельно, она совпадает с плоскостью ά, так как по аксиоме А1 через точки М, Р и Q проходит только одна плоскость.

Теорема доказана.

Теорема

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Доказательство

Рассмотрим прямые а и b, пере­секающиеся в точке М, и докажем, что через эти прямые проходит п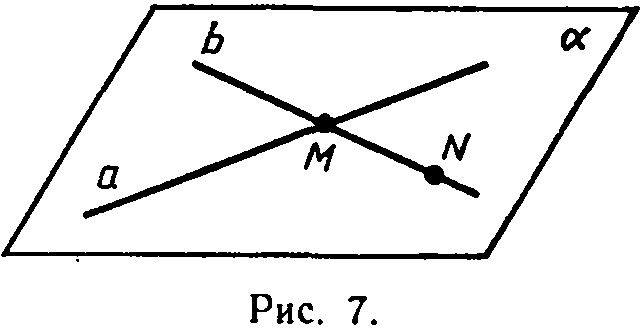 лоскость, и притом только одна.

О тметим на прямой b какую-нибудь точку N, отличную от точки М, и рассмотрим плоскость α, проходящую через точку N и прямую а. Так как две точки прямой b лежат в плоскости α, то по аксиоме А2 плоскость α проходит через прямую b. Итак, плоскость α проходит через прямые а и b. Единственность такой плоскости следует из того, что любая плоскость, проходящая через прямые а и b, проходит через точку N. Следовательно, она совпадает с плоскостью α, поскольку через точку N и прямую а проходит только одна плоскость.

Теорема доказана

2) Теорема о боковой поверхности правильной пирамиды

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Доказательство

Боковые грани правильной пирами­ды - равные равнобедренные треугольники, основания кото­рых — стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произ­ведений сторон основания на половину апофемы d. Вынося множитель 0,5d за скобки, получим в скобках сумму сторон основания пирамиды, т.е. его периметр.

Теорема доказана.

Б илет №2

1) Свойства параллельных плоскостей. Рассмотрим два свойства параллельных плоскостей.

1°. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Наглядным подтверждением этого факта служат линии пере­сечения пола и потолка со стеной комнаты — эти линии парал­лельны. Для доказательства данного свойства рассмотрим пря­мые а и b, по которым параллельные плоскости α и β пере­секаются с плоскостью µ. Докажем, что а||b. Эти прямые лежат в одной плоскости (в плоскости µ) и не пересекаются. В самом деле, если бы прямые а и b пересекались, то плоскости α и β имели бы общую точку, что невозможно, так как α||β. Итак, прямые а и b лежат в одной плоскости и не пересекаются, т. е. а||b.

2°. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Для доказательства этого свойства рассмотрим отрезки АВ и СD двух параллельных прямых, заключенные между парал­лельными плоскостями α и β. Докажем, что АВ = СD. Плоскость µ, проходящая через параллельные прямые АВ и СD, пересекается с плоскостями α и β по параллельным прямым АС и ВD (свойство 1°). Таким образом, в четырехугольнике АВDС противоположные стороны попарно параллельны, т. е. АВDС — параллелограмм. Но в параллелограмме противоположные сто­роны равны, поэтому АВ = СD.

чтд.

2) Призма. Рассмотрим два равных многоугольника А₁А₂... А_n и В₁В₂... В_n, расположенных в параллельных плос­костях ά и β так, что отрезки А₁В₁, А₂В₂....А_nВ_n , соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников:

А₁А₂В₂В₁ А₂А₃В₃В₂.....А_пА₁В₁В_п (1)

является параллелограммом, так как имеет попарно параллель­ные противоположные стороны. Например, в четырехугольнике А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию, а сторо­ны А₁А₂ и В₁В₂ — по свойству параллельных плоскостей, пере­сеченных третьей плоскостью.

Многогранник, составленный из двух равных многоугольни­ков А₁А₂...А_n и В₁В₂..В_n, р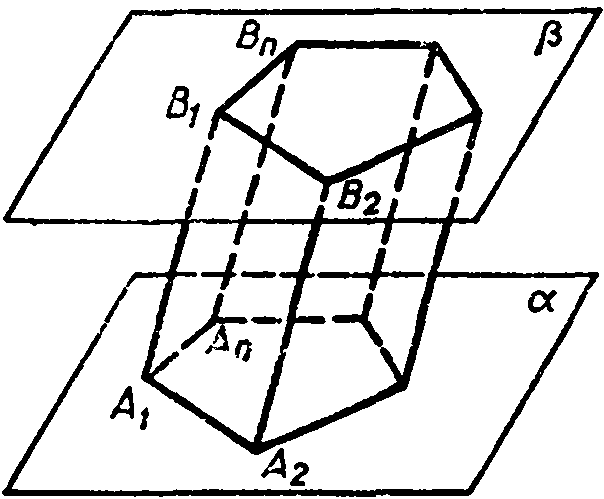 асположенных в параллельных плос-

костях, и п параллелограммов (1), называется призмой.

Многоугольники А₁А₂...А_n и В₁В₂...В_n называются основания­ми, а параллелограммы (1)—боковыми гранями призмы. От­резки А₁В₁, А₂В₂.....А_nВ_nназываются боковыми ребрами призмы.

Эти ребра как противоположные стороны параллелограммов (1), последовательно приложенных друг к другу, равны и параллель­ны. Призму с основаниями А₁А₂...А_n и В₁В₂...В_n обозначают А₁А₂... А_пВ₁В₂...В_n и называют n-угольной призмой. На рисунке изображена шестиугольная призма.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае — наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые гра­ни — равные прямоугольники.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности приз­мы — сумма площадей ее боковых граней. Площадь S_П0ЛН полной поверхности выражается через площадь S_бок боковой поверх­ности и площадь S_0СН основания призмы формулой

Sполн =Sбок+2Sосн

Докажем теорему о площади боковой поверхности прямой призмы.

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Доказательство

Боковые грани прямой призмы — прямоугольники, основания которых — стороны основания приз­мы, а высоты равны высоте H. призмы. Площадь боковой поверх­ности призмы равна сумме площадей указанных прямоугольни­ков, т. е. равна сумме произведений сторон основания на высоту H. Вынося множитель Н за скобки, получим в скобках сумму сторон основания призмы, т. е. его периметр Р. Итак, S_бoк=РН.

Теорема доказана.