2.Класифікаціяекономіко-математичнихмоделей. Етапипобудовиекономіко-математичних моделей.

В основу класифікаціїекономіко-математичних моделей покладенотакіознаки:

1) за цільовимпризначенням – теоретико-аналітичні та прикладнімоделі;

2) за ступенемагрегуванняоб’єктів – макроекономічні та мікроекономічні

3) за конкретнимпризначенням – трендові, оптимізаційні, імітаційні

4) за типом інформації, – аналітичні та ідентифіковані

5) за врахуванням фактора невизначеності – детерміновані та стохастичні

6) за характером математичногоапарату – матричнімоделі, моделілінійного та нелінійногопрограмування, кореляційно-регресійнімоделі, моделітеоріїмасовогообслуговування, моделісітковогопланування та керування, моделітеоріїігорі т.п.;

7) за типом підходу до систем, якідосліджуються – дескриптивнімоделі та нормативнімоделі

8) за структурою моделей та характером їхскладових – одно- та багатофакторнімоделі, статичні та динамічнімоделі, моделіпростої та складноїструктури;

9) за часовими характеристиками – довго-середнь- та короткотермінові

Процедуру побудовимоделі та підготовкууправлінськогорішення на основіекономіко-математичнихметодівможнапредставити з допомогою ряду взаємозв’язанихетапів:

1. Постановка задачі та формулювання мети дослідження. Описуваномуетапупередуєвиникненняпроблемнихситуацій, усвідомленняякихпризводить до необхідностіїхузагальненняабовирішення для майбутньогодосягненняпевногоефекту (корисності).

2. Побудоваконцептуальної (формалізованої) моделі. Базовою основою для побудовимоделіоб’єкта є його концептуальна модель. Відбуваєтьсяформалізаціяіснуючоїекономічноїпроблеми, яка полягає у вираженніїї з допомогоюматематичноїсимволікичерезвідповіднізалежності та відношення.

3. Формуванняінформаційноїбазимоделі. Третійетап є найбільштрудомістким, оскількивінпредставляє собою не тількипростийстатистичнийзбірінформації. Тут висуваютьсядоситьвисоківимоги до якості та достовірностіпідготовленоїінформації.

4. Побудовачисловоїекономіко-математичноїмоделі. На окресленомуетапінаосновіконцептуальноїмоделіздійснюєтьсяформуваннячисловоїматематичноїмоделіоб’єкта.

5. Числовийрозв’язокзадачі. Етапдослідженнячисловоїматематичноїмоделірозпочинається з їїаналізу (відношення до певногокласу моделей), виборувідповідного методу їїрозв’язання та програмногозабезпечення.

6. Аналізчисловихрезультатів і прийняттярішень. На цьомуетапівирішуєтьсяважливепитаннявідносноправильності та повнотирезультатівмоделювання, і, як результат, розробляютьсярекомендації для практичного використання при прийняттівигіднихрішеньабо для удосконаленнямоделі. Завершальнимкрокомпроцедурипобудовиекономіко- математичноїмоделі є оцінкаточностіодержанихрозрахунків та вироблення на їхосновіефективнихприкладнихрішень.

18.Актуальність задач цілочисельноголінійногопрограмування. Математична постановкацілочисельних задач лінійногопрограмування. Геометричнаінтерпретація на площині.

Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування.

До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Умова цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції. У даному розділі розглянемо задачі математичного програмування, в яких крім умови цілочисловості всі обмеження та цільова функція є лінійними, що мають назву цілочислових задач лінійного програмування.

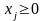
Загальна цілочислова задача лінійного програмування записується так: за умов: ; ; 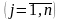— цілі числа .

Скажімо, множина допустимих розв’язків деякої нецілочислової задачі лінійного програмування має вигляд, зображений на рис. 6.1

Геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого на рис. 6.1 випадку множина допустимих планів складається з дев’яти точок (рис. 6.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох₁ та Oх₂ і проходять через точки з цілими координатами 0, 1, 2. Для знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’я­зок відповідає точці М ( ).

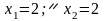Очевидно, особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.

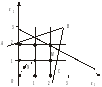
Рис 6.1 Рис 6.2

22. Транспортна задача. Метод потенціалів та умова існування оптимального розв’язку транспортної задачі.

Якщо транспортна задача є закритою, то вона завжди може бути розв’язана методом потенціалів.

Теорема. Якщо план X*= (x∗ij ) транспортної задачі є оптимальним, то

йому відповідає система із m + n чисел ui∗ і vj∗ , що задовольняють і умови:

ui∗ + vj∗ = cij для xij∗≥ 0 і

ui∗ + vj∗ ≤=cij для вільних значень xij∗=0 (i =1, 2,…, m; j =1, 2,…, n .)

Числа ui∗ й vj∗ називаються потенціалами відповідно постачальників і споживачів.

Алгоритм методу потенціалів складається з таких етапів:

1. Визначення типу транспортної задачі (відкрита чи закрита). За необхідності слід звести задачу до закритого типу.

2. Побудова першого опорного плану транспортної задачі одним з відомих методів.

3. Перевірка опорного плану задачі на виродженість. За необхідності вводять нульові постачання.

4. Перевірка плану транспортної задачі на оптимальність.

4.1. Визначення потенціалів для кожного рядка і стовпчика таблиці транспортної задачі. Потенціали опорного плану визначають із системи рівнянь ui + vj = cij, які записують для всіх запов¬нених клітинок транспортної таблиці, кількість яких дорівнює , а кількість невідомих — .

4.2. Перевірка виконання умови оптимальності для пустих клітин. За допомогою розрахованих потенціалів перевіряють умову оптимальності ui + vj  cij для незаповнених клітинок таблиці. Якщо хоча б для однієї клітини ця умова не виконується, тобто ui + vj > cij, то поточний план є неоптимальним, і від нього необхідно перейти до нового опорного плану.

4.3. Вибір змінної для введення в базис на наступному кроці. Загальне правило переходу від одного опорного плану до іншого полягає в тому, що з попереднього базису виводять певну змінну (вектор), а на її місце вводять іншу змінну (вектор), яка має покращити значення цільової функції

4.4. Побудова циклу і перехід до наступного опорного плану. Вибрана порожня клітина разом з іншими заповненими становить , отже, з цих клітин обов’язково утвориться цикл. У межах даного циклу здійснюють перерахування, які приводять до перерозподілу постачань продукції. Кожній вершині циклу приписують певний знак, причому вільній клітинці — знак «+», а всім іншим — за черговістю знаки «–» та «+». У клітин¬ках зі знаком «–» вибирають значення  і переносять його у порожню клітинку. Одночасно це число додають до відповідних чисел, які містяться в клітинках зі знаком «+», та віднімають від чисел, що позначені знаком «–». Якщо значенню  відповідає кілька однакових перевезень, то при відніманні залишаємо у відповідних клітинках нульові величини перевезень у такій кількості, що дає змогу зберегти невиродженість опорного плану.

Отже, клітинка, що була вільною, стає заповненою, а відповід¬на клітинка з мінімальною величиною xij вважається порожньою. У результаті такого перерозподілу перевезень продукції дістанемо новий опорний план транспортної задачі.

5. Перевірка умови оптимальності наступного опорного плану. Якщо умова оптимальності виконується — маємо оптимальний план транспортної задачі, інакше необхідно перейти до наступного опорного плану.