3.3. Случайные погрешности
При оценке случайных погрешностей результаты измерений и их ошибки рассматриваются как случайные величины. Универсальными характеристиками случайных величин являются функции распределения – интегральные и дифференциальные.
Интегральная
функция распределения F(x)
– это величина, определяющая вероятность
того (события), что случайная величина
в i-м опыте примет
значение, меньшее х, т.е.:
. (3.7)
Свойства интегральной функции распределения:
она положительна, т.е.
;неубывающая, т.е.
,
если
;
;
,
или
.;вероятность попадания случайной величины х в интервал от
до
равна разности
и
,
т.е.
.
Производная от интегральной функции распределения по случайной величине х называется дифференциальной функцией распределения плотности вероятности:
. (3.8)
Дифференциальная функция распределения определяет вероятность попадания случайной величины в бесконечно малый интервал от x до x + dx, отнесенную к величине этого интервала, т.е. к dx.
F
1
0 X
f
f
(xp)
X
Рис. 3.1. Интегральная и дифференциальная функции распределения
Свойства дифференциальной функции распределения:
она положительна, т.е.
;ее значение изменяется от 0 до 1 -
;площадь под линией
в интервале
равна единице, т.е.
- условие нормировки – вероятность
попадания величины х в интервал
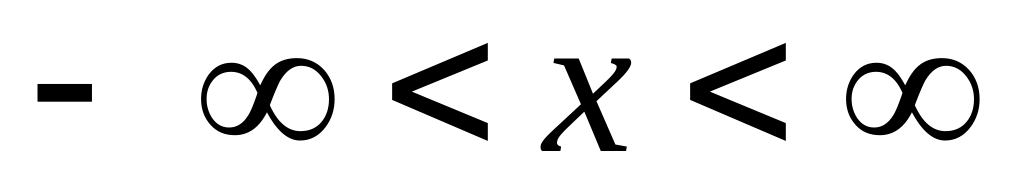равна единице. Такое событие называют
достоверным;
вероятность попадания случайной величины х в интервал от
до
определяется интегралом:
.
Графически эта вероятность определяется
площадью фигуры между линией
и осью абсцисс между ординатами
и
(см. рис. 3.1).
В статистике используют такие понятия, как квантиль, мода, медиана, математическое ожидание.
Квантиль
– значение случайной величины х,
которому отвечает вероятность ее
появления
,
т.е.
.
Мода
– наиболее вероятное значение случайной
величины, т.е.
.
По количеству максимумов функции
распределения могут быть одномодальными,
двухмодальными и т.д.; при равномерном
распределении, т.е. при
=
const, мода отсутствует.
Медиана
(50% квантиль) - значение случайной
величины, вероятность получения которой
равна ½ (50%). Медиана делит всю совокупность
значений случайной величины на две
равные части по количеству полученных
результатов.
Математическое
ожидание
- значение случайной величины, определяющее
центр фигуры, лежащей под линией
:
.
Распределения могут быть симметричными и несимметричными. При симметричном распределении ветви функции располагаются симметрично относительно ординаты, проходящей через моду , а числовые значения моды , медианы и математического ожидания совпадают. При несимметричном – нет.
3.3. Нормальный закон распределения (закон Гаусса)
Нормальный закон реализуется при воздействии на случайную величину большого количества независимо действующих факторов, каждый из которых оказывает незначительное влияние на результат по сравнению с суммарным влиянием всех факторов. Математически нормальный закон описывается уравнением:
, (3.9)
где
- генеральная дисперсия; -
генеральное среднее квадратичное
отклонение;
- математическое ожидание случайной
величины.
Величины и являются параметрами нормального закона, поэтому он относится к классу двухпараметрических законов распределения.
X
=
Рис. 3.2. Параметры нормального закона распределения
Свойства нормального закона:
большие отклонения случайной величины от ее математического ожидания маловероятны;
точки перегиба отстоят от математического ожидания на величину среднего квадратичного отклонения см. рис. 3.2.
площадь фигуры, заключенной между кривой , осью абсцисс и ординатами - и + равна 0,683, т.е. вероятность отклонения случайной величины от ее математического ожидания на величину составляет 68,3%.
Значения
по формуле (3.9) зависят от параметров
и .
С
изменением
математического ожидания
происходит смещение положения моды
вдоль оси Х;
изменение дисперсии
(и среднего квадратичного отклонения
)
является
причиной изменения высоты и ширины
фигуры
так, что площадь, лежащая под линией
остается неизменной и равной 1.
Замена в формуле (3.9) размерной переменной х на нормированную t = (x - )/ дает нормированное нормальное распределение
, (3.10)
графическое
изображение которого одинаково для
всех значений
и
.
Интегральная функция нормированного распределения определяется формулой:
,
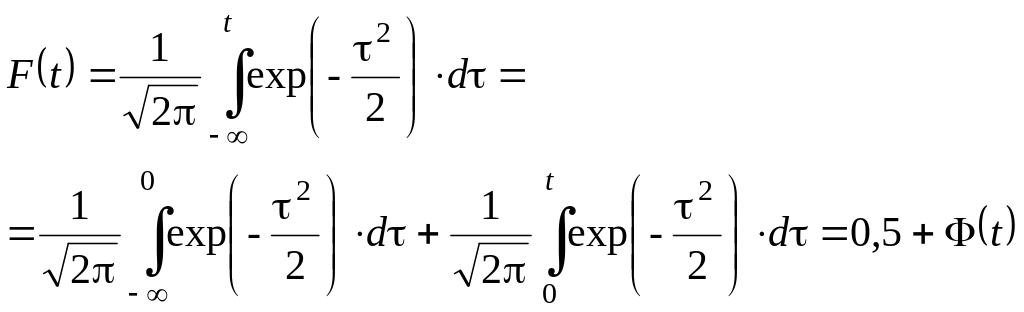(3.11)
где
;
- функция
Лапласа
(табличный интеграл).
Свойства функции Лапласа:
; 
; 
; 
.
Вероятность попадания случайной величины Х в интервал от до может быть найдена по таким формулам:
, (3.12)
где
; 
.