Наближені формули периметра
YNOT:
,
де
Максимальна
похибка цією формули становить близька
0,3619% при ексцентриситеті еліпса 0,979811
(відношення осей ~1/5). Похибка завжди
додатна.
Дуже
наближена формула:
Дотична
Рівняння
дотичної
до еліпса через точку
,
яка належить еліпсу
Гіпербола
Гіпербола (грец. Ὑπερβολή) — кривВизначення
Гіпербола є невиродженою кривою другого порядку, яка задається рівнянням:[1]
де
та
—
параметри. Таке рівняння називається
канонічним рівнянням
гіперболи.[2]
Нехай канонічне рівняння кривої другого порядку шляхом переносу центру координат перетворено у вигляд:
В
цьому випадку крива проходить через
початок координат нової системи; вісь
абсцис є віссю симетрії кривої. Це
рівняння відображає той факт, що
невироджена крива другого порядку є
геометричним місцем точок, відношення
відстаней яких
(ексцентриситет)
від заданої точки (фокуса)
та від заданої прямої (директриса)
незмінна. Крива є гіперболою, якщо
.[1]
Тобто, гіпербола є геометричним місцем
точок, абсолютна величина різниці
відстаней яких від фокусів дорівнює
(фокальна
властивість гіперболи). Директоріальна
властивість гіперболи полягає в тому,
що гіпербола є геометричним місцем
точок, відношення відстаней яких від
фокуса до одноіменної директриси
дорівнює
.[2]
Властивості
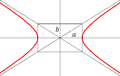
Гіпербола та її фокуси.
Гіпербола та її напіввіссі та асимптоти.
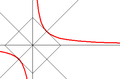
Рівнобічна гіпербола.
|
Якщо
в канонічному рівнянні гіперболи
,
то гіпербола називається рівнобічною.
В координатах
рівняння рівнобічної гіперболи
матиме вигляд:
звідки
випливає, що по відношенню до координат
та
рівнобічна
гіпербола представляє собою графік
звортньо-пропорційної
залежності. В
координатах
та
маємо
такий саме графік обернений на кут
.[2]
При
(а
також при
)
графік звортньо-пропорційної залежності
щільніше притіскається до осі абсцис
(відповідно,
до осі ординат
),
оскільки ці осі є асимптотами
(двобічними) графіку. В канонічних
координатах
,
ці
асимптоти є бісектрисами
та
координатних
кутів.[2]
З гіперболою пов'язані такі числові властивості:
число , що зветься дійсною напіввіссю;
число , що зветься уявною напіввіссю;
число
,
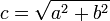що зветься лінійним
ексцентриситетом;число
,
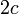що зветься фокусною
відстаню;число
,
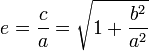що називається числовим
ексцентриситетом;число
,
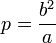що зветься фокальним
параметром;вісь абсцис, що зветься дійсною (або фокальною) віссю;
вісь ординат, що зветься уявною віссю;
точка
,
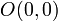що зветься центром;точки
,
що звуться вершинами;точки
,
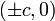що звуться фокусами;прямі
,
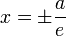що звуться директрисами.
а другого порядку з ексцентриситетом більшим за одиницю.
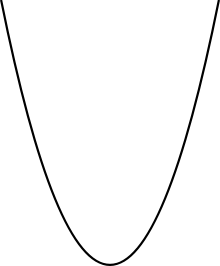
Парабола
Пара́бола (від грец. παραβολή) — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку.
Точка зветься фокусом, а пряма - директрисою.
Парабола, гіпербола та еліпс є конічними перерізами. Парабола є конічним перерізом з одиничним ексцентриситетом.Якщо точкове джерело світла розміщене у фокусі параболоїдного дзеркала, то відбиті від поверхні промені будуть розповсюджуватися паралельно.
Графік функції, що задається за допомогою поліному другого порядку від однієї змінної являє собою параболу.
