Дослідження стійкості нелінійних систем

Стійкість нелінійних систем є значно більш складним поняттям, ніж стійкість лінійних систем. Стійкість лінійних систем, для яких виправдовується принцип суперпозиції, є їх властивістю, тобто вимога стійкості до системи визначає структуру та значення її параметрів. При цьому фіксовані стани системи у визначені моменти часу і вхідні сигнали не мають ніякого значення. Лінійна система є або стійкою, або нестійкою і для дослідження стійкості існують порівняно прості математичні методи.

У зв’язку з тим, що у нелінійних системах може існувати особливий вид усталеного режиму – автоколивання, то необхідно дати коректне визначення стійкості. Таке визначення дав А.М.Ляпунов:

Незбурений рух стійкий, якщо при достатньо малих відхиленнях збурений рух наскільки завгодно мало відрізняється від незбуреного. При цьому система асимптотично стійка, якщо збурений рух прямує до незбуреного.

Для нелінійних систем розрізняють різні види стійкості в залежності від величини зовнішнього впливу:

- стійкість у "малому" – це стійкість системи при безмежно малих відхиленнях від усталеного режиму;

- стійкість у "великому" – стійкість при великих але обмежених відхиленнях (зовнішніх впливах) від усталеного режиму;

- стійкість у "цілому" – стійкість при будь-яких необмежених відхиленнях.

Стійкість називається асимптотичною, якщо система повертається до вихідного стану, тобто в ту саму точку з якої її вивів зовнішній вплив.

Стійкість називається неасимптотичною, якщо система повертається в деяку точку в певному околі від вихідного режиму.

Абсолютна стійкість – стійкість цілого класу нелінійних систем, які мають таку нелінійність, яку можна вкласти в межі певного кута.

Перший непрямий метод дослідження стійкості Ляпунова. Використовується для дослідження стійкості в "малому". Він полягає в тому, що нелінійну систему лінеаризують, використовуючи розклад в ряд Тейлора. Тоді нелінійна система стійка, якщо лінеаризована система також стійка, і навпаки. Проте, якщо лінеаризована система виявиться на межі стійкості, то про стійкість нелінійної системи судити по ній не можна.

Для нелінійних систем вирішення питання стійкості є досить складним. Наприклад, рух або рівновага, стійкі у малому, можуть з’явитися нестійкими при великих відхиленнях. З іншого боку, при одних і тих самих вхідних сигналах система може мати декілька рівноважних станів. Тобто перший метод Ляпунова, що ґрунтується на дослідженні стійкості за рівняннями першого наближення, є недостатнім для повного дослідження стійкості нелінійних систем. Унаслідок цього для дослідження стійкості “у великому” і “у цілому” використовують спеціальні методи, до яких належать другий (прямий) метод Ляпунова та критерій стійкості Попова.

Другий (прямий) метод Ляпунова. Метод ґрунтується на побудові спеціальних функцій Ляпунова, які дозволяють отримати достатні умови стійкості рівноваги "у великому". Дані функції V мають зміст відстані у спеціальному просторі станів між досліджуваним незбуреним і збуреним рухами. Якщо з часом ця функція спадає, тобто , то незбурений рух стійкий, а при - нестійкий.

Дослідження стійкості зводиться до аналізу швидкості зміни функції V. Умови стійкості сформульовані у двох теоремах Ляпунова.

Теорема 1. Якщо існує знаковизначена функція , похідна якої за часом у силу диференціальних рівнянь руху є знакопостійною функцією протилежного з V знаку, або тотожно дорівнює нулю, то незбурений рух стійкий.

Теорема 2. Якщо, крім того, функція знаковизначена, то незбурений рух стійкий асимптотично.

Відзначимо, що знакопостійною називається функція, яка при всіх значеннях своїх аргументів набуває значення тільки одного знаку або нульове значення. Знаковизначеною називається знакопостійна функція, яка набуває нульове значення тільки при нульовому значенні всіх її аргументів (на початку координат).

Складність даного методу полягає у тому, що задача вірного вибору функції Ляпунова пов’язана зі складнощами. Відсутні загальні методи побудови цих функцій. Більше того, зустрічаються випадки, коли система є стійкою, а внаслідок невірно вибраної функції Ляпунова цей факт установити не вдається. У такому випадку для розв’язання технічних задач метод Ляпунова не є досить ефективним.

Критерій стійкості Попова. Важливою особливістю загальної теорії стійкості нелінійних систем є те, що розглядаються не конкретні види функцій (параболи, експоненти тощо), а класи функцій, які задовольняють тим чи іншим обмеженням. Якщо стан рівноваги системи асимптотично стійкий "у цілому" при будь-якій нелінійній функції із заданого класу, то вона називається абсолютно стійкою у цьому класі. Будемо розглядати клас функцій, що задовольняють секторним обмеженням. Їх характеристики на площині вміщаються у кутовому секторі, що утворений двома прямими: і , (k₂  k₁).

Кажуть, що такі нелінійності належать до класу ( ). Можна виділити деякі підкласи цього класу:

- підклас ( ) задовольняє умовам:

.

Тобто, нелінійність має будь-який контур, який не виходить за межі заданого кута .

- підклас ( ) – будь-яка , що розташована тільки у першому і третьому квадрантах площини (x; y).

.

Дослідження абсолютної стійкості рівноваги системи з нелінійністю із підкласу ( ) досить просто виконується за допомогою частотного методу, запропонованого румунським вченим В.М. Поповим (1959 р.). При цьому припускається, що лінійна частина системи стійка та її комплексна передаточна функція має вигляд:

.

Введемо поняття перетвореної комплексної передаточної функції лінійної частини:

,

у якої дійсна частина така сама, як у , а уявна – .

Тоді можна дати таке геометричне трактування критерію Попова:

Система зі стійкою лінійною частиною абсолютно стійка у класі стаціонарних нелінійних характеристик y = (x) підкласу ( ), якщо через точку –1/k на дійсній осі комплексної площини можна провести пряму так, щоб перетворена частотна характеристика знаходилась праворуч від цієї прямої.

На рис. +++ а), б) наведені випадки, коли умова Попова виконується, а на рис. +++, в) – не може бути виконана.

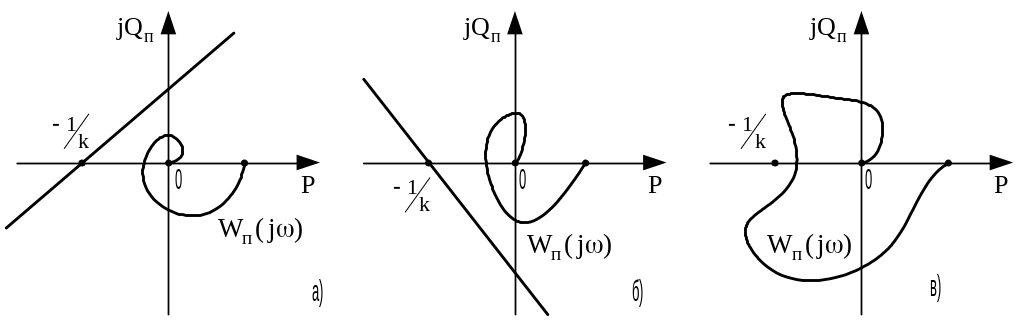
Рис. +++ - Ілюстрація критерію Попова

Загальні поняття про коректування нелінійних систем

Коректування нелінійних САК здійснюється з метою забезпечення стійкості або з метою отримання автоколивань із заданими амплітудою та частотою. Коректування можна здійснити зміною характеристик як лінійної частини, так і нелінійного елемента.

Зміна характеристики лінійної частини досягається відомими способами:

- увімкненням послідовних коректувальних пристроїв (введення похідних та інтегралів до законів регулювання);

- увімкненням зустрічно-паралельних коректувальних пристроїв (уведення жорстких і гнучких зворотних зв’язків, інерційних і безінерційних);

- увімкненням коректувальних пристроїв за збуренням (комбіноване керування).

Зміна характеристики нелінійного елемента може бути досягнута декількома способами. Деякі статичні нелінійності можна компенсувати за допомогою відповідних обернених нелінійностей. Для цього паралельно або послідовно з основною нелінійністю вмикають компенсуючу нелінійність, яка має обернену характеристику . Еквівалентне з’єднання при цьому буде лінійним.

Під час зміни характеристики нелінійного елемента слід з’ясувати вплив різних нелінійностей регулятора на процес автоматичного керування. Розглянемо основні з них.

Ширина зони нечутливості. У більшості випадків збільшення цього параметра сприяє заспокоєнню коливань, тобто покращується стійкість системи, але при цьому з’являються додаткові усталені помилки, зокрема, статична помилка, яка пропорційна ширині зони нечутливості.

У багатоконтурній системі зона нечутливості може завдати й інших неприємностей, тобто, при охопленні зворотним зв’язком вона може утворити петльову характеристику, що сприяє утворенню автоколивань.

Характеристика з обмеженням вихідної величини. У випадку, якщо (табл. 1.1, 2), ланка працює як лінійна, значить, дана нелінійність грає роль лише при досить великих вхідних величинах : .

Така характеристика в одноконтурній системі регулювання, змінюючи форму кривої перехідного процесу при значних відхиленнях, як правило, не впливає на межу стійкості системи. Позитивний її вплив полягає у тому, що вона робить межу стійкості системи “безпечною”. Пояснимо це таким чином. На самій межі стійкості у лінійній системі (при ) мають місце періодичні коливання. За цією межею коливання розходяться, причому розходяться до нескінченності. У нелінійній системі ці коливання будуть розходитися за лінійним законом тільки до . Далі, при , вихідна величина y буде обмежена сталою . Це буде аналогічно якби зниженню загального коефіцієнта підсилення регулятора, внаслідок чого розкачування коливань припиниться.

Такий вплив нелінійних характеристик з обмеженням або насиченням в одноконтурній системі. У багатоконтурних системах, тобто у системах із додатковими зворотними зв’язками, вплив цих нелінійних характеристик може бути негативним, особливо якщо така характеристика охоплюється зворотним зв’язком. Вона може викликати звуження зони стійкості й погіршення якості перехідного процесу порівняно з такою самою багатоконтурною лінійною системою.

Ширина гістерезисної петлі. У більшості випадків поява гістерезисної петлі у одноконтурній системі сприяє коливанням з тим більшою амплітудою, чим більша ширина петлі, що є негативним наслідком. Петлю можна розцінювати як специфічний нелінійний вираз запізнення. Якщо така нелінійність входить до складу додаткового зв’язку регулятора, то запізнення, що вводиться цією нелінійністю до зворотного зв’язку, може позитивно впливати на якість процесу керування у багатоконтурній системі подібно інерційному зворотному зв’язку.

Зазначимо також додаткові особливості введення зворотного зв’язку в релейних системах регулювання:

- уведення жорсткого зворотного зв’язку у релейний регулятор (таке, щоб реле входило до числа ланок, що охоплюються зворотним зв'язком) може перетворити розривний релейний закон регулювання у безперервний, приблизно лінійний. Це дозволяє застосовувати до нелінійної системи у першому наближенні звичайні лінійні методи розрахунку;

- уведення гнучкого зворотного зв’язку при вдалому підборі параметрів також дозволяє отримати безперервний лінійний закон регулювання, але швидкісний (астатичний);

- жорсткий зворотний зв’язок у релейній системі регулювання є сильним засобом пригнічення автоколивань, при цьому зі збільшенням коефіцієнта зворотного зв’язку розширюється зона стійкості рівноважного стану системи та прискорюється затухання перехідних процесів.

Слід зазначити також, що всі види нелінійності не тільки мають враховуватися, але часто їх можна використовувати спеціально, як нелінійні коректувальні засоби для покращання процесу регулювання.

Моделювання нелінійних систем

Протилежно до теорії лінійних систем, яка є наочною та поширеною внаслідок її завершеності, розробка теорії та методів аналізу нелінійних систем скрутна через значну багатогранність форм нелінійностей і відсутність універсальних принципів, таких, як принцип суперпозиції для лінійних систем.

Тому всі розглянуті методи аналізу нелінійних САК мають обмежене використання:

- методи лінеаризації дозволяють використовувати при розрахунках переваги лінійної теорії, але вони обмежені допустимою зоною зміни сигналів, у межах якої лінеаризація є справедливою і можливою;

- метод фазової площини обмежується аналізом систем другого порядку з постійними вхідними сигналами;

- теорія функцій Ляпунова не має обмежень, але підбір правильних функцій Ляпунова стає складною задачею.

Складні нелінійні системи, які застосовують для керування з високою точністю, за допомогою наведених методів досліджувати не можна. Для цього слід використовувати моделювання, тобто відтворення систем і сигналів на аналогових чи цифрових ЕОМ. Аналогові, цифрові та гібридні ЕОМ, що застосовуються для моделювання, мають специфічні властивості.

Важлива проблема для всіх методів моделювання полягає в тому, щоб процес розрахунку завжди починався за заданих початкових умов, оскільки від цього залежить поведінка нелінійної системи. Тому постає необхідність визначення прийнятних початкових умов на базі грубого аналізу системи за допомогою відомих наближених методів.

Випадкові процеси в автоматичних системах управління

При попередніх розрахунках ми припускали, що зовнішні впливи (керуючі дії та збурення), є визначеними відомими функціями часу. У цих випадках стан системи, що описується звичайними диференціальними рівняннями, у будь-який момент часу t однозначно визначається станом системи у попередній момент часу t₀ < t. Звичайно вибирають t₀ = 0 і кажуть, що стан системи однозначно визначається початковими умовами і може бути точно передбаченим для будь-якого моменту часу t. Такі системи називаються детермінованими.

Однак на практиці часто зустрічаються впливи, закон зміни яких має випадковий характер і не може бути наперед точно визначений. Такими випадковими впливами є, наприклад, добові зміни навантаження енергосистеми; пориви вітру, що діють на літак; удари хвиль у гідродинамічних системах; флуктуаційні шуми у радіотехнічних пристроях тощо. При випадкових впливах даних про стан системи у момент t₀ недостатньо, щоб судити про її стан у подальший момент часу t > t₀.

Випадкові дії можуть прикладатися до системи зовні (зовнішні дії) або виникати усередині деяких її елементів (внутрішні шуми). Випадкові зміни властивостей системи звичайно можна звести до еквівалентного впливу деяких випадкових завад, що діють на неї, тому далі будемо вважати, що на систему діють тільки зовнішні випадкові впливи.

Розрахунок систем автоматичного управління при випадкових діях виконують за допомогою спеціальних статистичних методів. САУ, що спроектована на основі цих методів, буде забезпечувати виконання вимог, до цієї системи не тільки для одного детермінованого впливу, а для цілої сукупності впливів, що задані за допомогою статистичних характеристик.

Статистичні методи дозволяють з’ясувати лише закономірності, що є притаманними випадковим явищам масового характеру. Наприклад, якщо помилка системи має випадковий характер, то точне її значення у будь-який момент часу за допомогою статистичного розрахунку передбачити неможливо. Однак, якщо провести багато вимірювань помилки у однакових умовах, то, наприклад, середнє значення помилки шляхом статистичного розрахунку можна передбачити з достатньою точністю.

Випадкові процеси та їх основні статистичні характеристики

Функція, значення якої при кожному значенні незалежної змінної є випадковою величиною, називається випадковою функцією. Випадкові функції, для яких змінною є час t, називають випадковими процесами або стохастичними процесами.

Якщо, наприклад, проведено n окремих випробувань, то у результаті випадковий процес X(t) може прийняти n різних невипадкових (регулярних) функцій часу x_i(t), де і = 1, 2, ..., n. Будь-яка з цих функцій x_i(t), якій, у результаті випробування, виявився рівним випадковий процес X(t) називається реалізацією випадкового процесу (або можливим значенням випадкового процесу). Сказати наперед, за якою з реалізацій піде процес, неможливо.

Розглянемо, наприклад, випадковий дрейф на виході підсилювача постійного струму при вхідній напрузі, що дорівнює нулю. Щоб вивчити характеристики дрейфу, можна узяти n однакових підсилювачів, помістити їх у однакові умови роботи, одночасно увімкнути і отримати n осцилограм дрейфу на виходах підсилювачів. Кожна з осцилограм є конкретною реалізацією x_i(t) випадкового процесу X(t). Для будь-якого фіксованого моменту часу t = t₁ реалізація випадкового процесу x_i(t₁) є конкретною величиною, а значення випадкової функції X(t₁) є випадковою величиною, що називається перерізом випадкового процесу у момент часу t₁. Тому не можна стверджувати, що випадковий процес у даний момент часу має деяке детерміноване значення, можна говорити лише про ймовірність того, що у даний момент часу значення випадкового процесу, як випадкової величини, буде знаходитись у певних границях.

Статистичні методи вивчають не кожну з реалізацій x_i(t), що утворюють множину X(t), а властивості всієї множини у цілому. Тому під час дослідження автоматичної системи управління роблять висновок про її поведінку не відносно до будь-якого певного впливу, а відносно до цілої сукупності впливів.

Статистичні властивості випадкової величини х визначають за її функцією розподілу (інтегральним законом розподілу) F(x) або за щільністю ймовірності (диференціальним законом розподілу) w(x).

Випадкові величини можуть мати різні закони розподілу: рівномірний, нормальний, експоненціальний тощо. У багатьох задачах автоматичного керування дуже часто використовують нормальний закон розподілу (закон Гауса), який має місце, якщо випадкова величина визначається сумарним ефектом від впливу великої кількості різних незалежних факторів.

З курсу теорії ймовірності відомо, що випадкова величина х при нормальному законі розподілу повністю визначається математичним сподіванням (середнім значенням) m_x і середнім квадратичним відхиленням _х.

Аналітичний вираз функції розподілу у цьому випадку має вигляд:

(2.1)

Аналітичний вираз щільності ймовірності для нормального закону розподілу:

(2.2)

Для випадкового процесу використовують також поняття функції розподілу F(x, t) і щільності ймовірності w(x, t), що залежать від фіксованого моменту часу t і від деякого вибраного рівня х, тобто є функціями двох змінних: х і t.

Розглянемо випадкову величину X(t₁), тобто переріз випадкового процесу у момент часу t₁. Одномірною функцією розподілу (функцією розподілу першого порядку) випадкового процесу X(t) називають ймовірність того, що поточне значення випадкового процесу X(t₁) у момент часу t₁ не перевищує деякого заданого рівня (числа) х₁, тобто:

(2.3)

Якщо функція F₁(x₁, t₁) має частинну похідну за х₁, тобто:

(2.4)

то функцію w₁(x₁, t₁) називають одномірною щільністю ймовірності (щільністю ймовірності першого порядку) випадкового процесу.