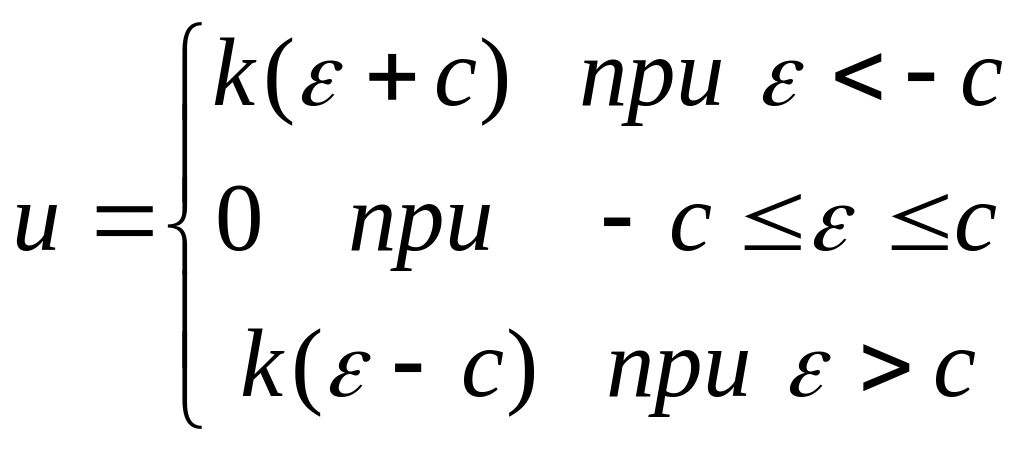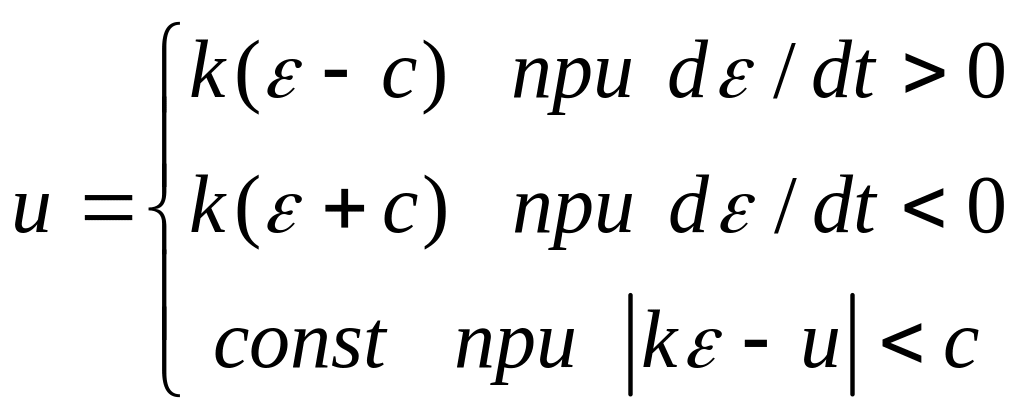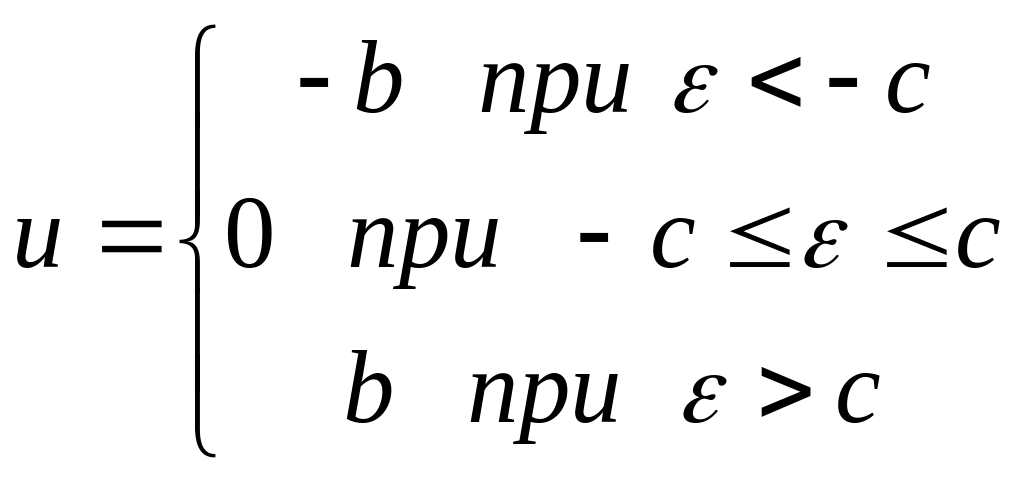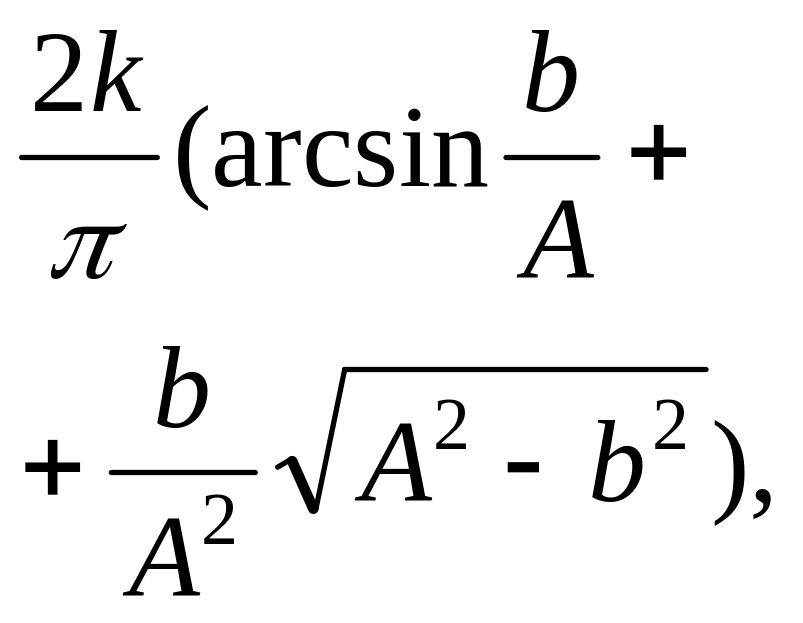Конспект лекцій

(рукопис)

з дисципліни

«Теорія автоматичного управління спеціальними системами»

Упорядник Христюк А.О.

Зміст

Нелінійні системи та їх аналіз
Випадкові процеси в автоматичних системах управління

Нелінійні системи та їх аналіз

Нелінійні системи – це системи, що описуються нелінійними диференціальними рівняннями. Система автоматичного управління (САУ) називається нелінійною, якщо до її складу входить хоча б один нелінійний елемент. На практиці найчастіше зустрічаються системи з безінерційними нелінійними елементами. Нелінійності в таких системах автоматичного керування зумовлені нелінійними статичними характеристиками елементів, що входять до складу системи. Такими елементами, зазвичай, є релейні елементи, в яких вихідна величина змінюється стрибкоподібно при неперервній зміні вхідної величини, логічні перемикаючі пристрої, які дозволяють змінювати структуру системи залежно від значення деяких її координат, підсилювачі із насиченням, в яких відбувається обмеження координат, машини та механізми з мертвими зонами і люфтами тощо.

Ми будемо розглядати вузький клас нелінійних САУ, що характеризуються такими особливостями:

- САУ складається з лінійної частини, яка описується лінійним диференціальним рівнянням із постійними коефіцієнтами, і нелінійного елемента;

- нелінійний елемент є безінерційним, і його вхідна та вихідна величини пов’язані нелінійними алгебраїчними рівняннями;

- нелінійних елементів може бути декілька, але вони не повинні розділятись лінійними інерційними ланками.

Нелінійні системи, в порівнянні з лінійними, мають ряд принципових особливостей. Зокрема, такими особливостями є:

- не виконується принцип суперпозиції, і дослідження нелінійної системи при декількох впливах не можна зводити до дослідження при одному впливі;

- стійкість та характер перехідного процесу залежать від величини початкового відхилення від положення рівноваги;

- при фіксованих зовнішніх впливах можливі декілька (а іноді і безліч) положень рівноваги;

- у нелінійних системах виникають вільні усталені процеси, які в лінійних системах неможливі (наприклад, автоколивання).

Універсальих аналітичних (математичних) методів дослідження нелінійних систем не існує. В процесі розвитку теорії автоматичного управління було розроблено різні математичні методи аналізу та синтезу нелінійних систем, кожен з яких може бути застосованим до певного класу систем та задач. Найбільш широко застосовними методами дослідження нелінійних систем є:

- метод фазового простору (площини);

- метод функцій Ляпунова;

- метод гармонічної лінеаризації (метод гармонічного балансу);

- методи дослідження абсолютної стійкості.

Будь-яке дослідження більш чи менш складних нелінійних систем, як правило, закінчується математичним моделюванням. І у цьому відношенні математичне моделювання є одним із універсальних (не аналітичних) методів дослідження.

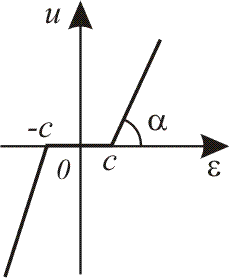
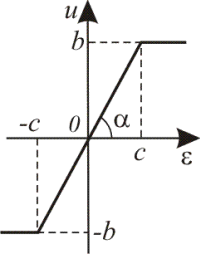
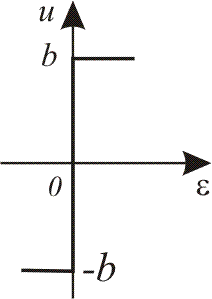
Статичні характеристики нелінійних елементів.

Більшість статичних характеристик реальних нелінійних елементів може бути зведена до обмеженого числа типових. Характеристики типових нелінійних елементів зведено в табл. 1.1.

Таблиця 1.1.

№	Назва елемента	Характеристика	Математичний опис
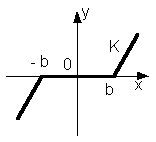
1	Ланка із зоною нечутливості
2	Пропорційна ланка із насиченням
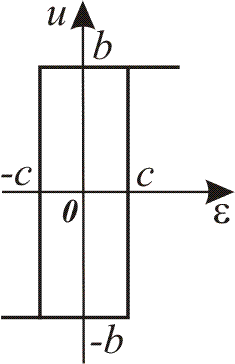
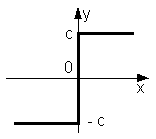
3	Ідеальне двопозиційне реле
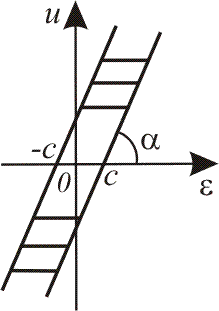
4	Характеристика з люфтом
5	Ідеальне трипозиційне реле
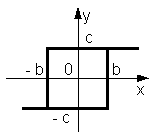
6	Реальне двопозиційне реле

У керуючих пристроях автоматичних систем поряд з релейними елементами використовуються так звані особливі нелінійності: добуткова ланка, елементи зі змінною структурою, елементи логічного типу.

Добуткова ланка використовується в обчислювальних блоках систем для обчислення квадрату сигналу і для визначення модуля сигналу.

Використання керуючих пристроїв зі змінною структурою створює великі можливості для покращення якості систем. У таких пристроях до основного контуру системи залежно від визначених умов вмикається або лінійна ланка W₁, або лінійна ланка W₂.

Нелінійності логічного типу залежно від комбінацій значень вхідних змінних видають сигнал, що дорівнює +1, -1 або 0.

Види з’єднань нелінійних елементів та розрахунок сумарних характеристик.

Якщо у систему входить декілька нелінійних елементів, з’єднаних послідовно, паралельно або зустрічно-паралельно, то сумарну характеристику можна побудувати за певними правилами.

П аралельне з’єднання нелінійних елементів. При паралельному з’єднанні нелінійних елементів сумарну характеристику будують як геометричну суму нелінійних характеристик окремих елементів (рис. 1.1).

Послідовне з’єднання двох нелінійних елементів. При послідовному з’єднанні нелінійних елементів, вихідна величина одного нелінійного елемента є вхідною для наступного нелінійного елемента (рис. 1.2 а). Тому під час побудови сумарної нелінійної характеристики систему координат другої характеристики повертають на 90^, сполучаючи осі і .

У першій чверті будують характеристику НЕ1, в другій – НЕ2, в третій проводять бісектрису, за допомогою якої у четвертій чверті отримують сумарну нелінійну характеристику (рис. 1.2 б).

З’єднання нелінійних елементів зі зворотнім зв’язком.

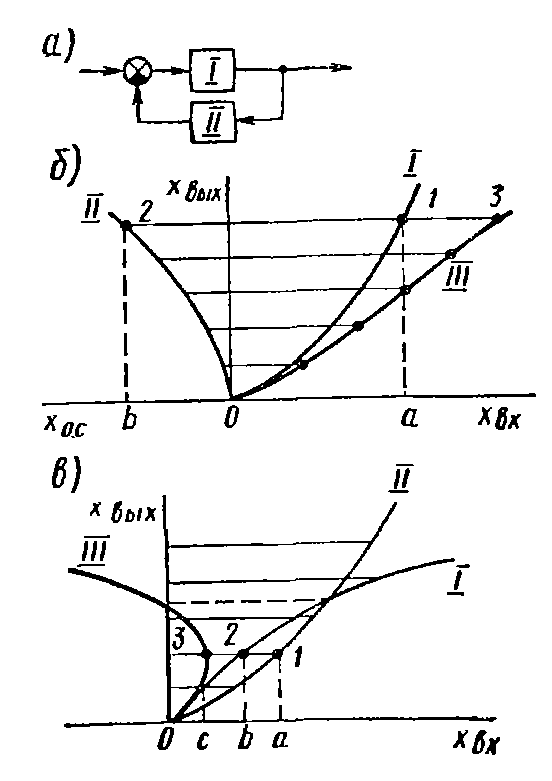
Рис. 1.3. а) структурна схема з’єднання елементів зі зворотнім звязком; б) побудова сумарної (ІІІ) нелінійної характеристики; в) побудова сумарної (ІІІ) нелінійної характеристики при додатньому зворотньому звязку

При побудові результуючої характеристики нелінійного елемента НЕ1, охопленого нелінійним зворотнім зв’язком з характеристикою НЕ2 (рис. 1.3 а) в першому квадранті будуємо характеристику елемента НЕ1, а в другому – елемента НЕ2, повернувши систему координат протигодинникової стрілки на 90 градусів (щоб вісь вихідного сигналу НЕ1 співпала з віссю вхідного сигналу НЕ2). В цьому випадку результуюча характеристика отримається як геометрична сума характеристик НЕ1 та НЕ2, просумованих в напрямку осі х_вх.

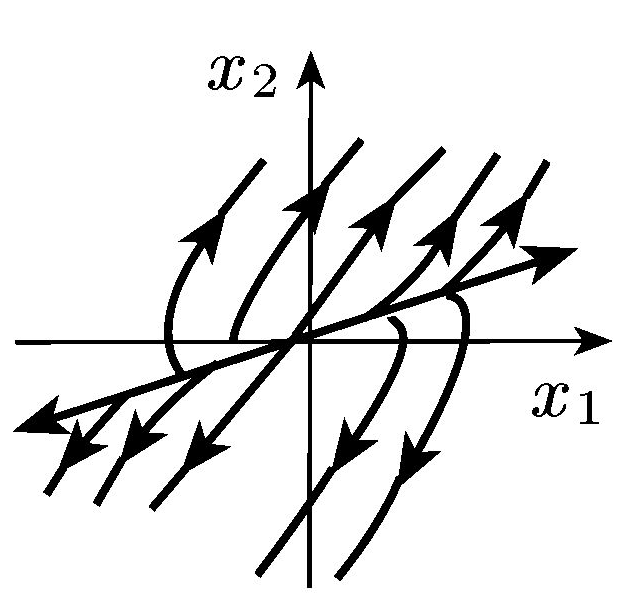
Зображення процесів на фазовій площині

Якщо рівняння системи представлені у нормальній формі, то вектор стану системи однозначно визначає її стан. Кожному стану системи в просторі станів відповідає точка. Точка, яка відповідає поточному стану системи називається зображуючою точкою. При зміні стану зображуюча точка описує траекторію. Ця траекторія називається фазовою траекторією. Сукупність фазових траекторій, яка відповідає різним можливим початковим умовам, називається фазовим портретом.

Наочно фазову траекторію та фазовий портрет можна представити у випадку двомірного фазового простору. Двомірний фазовий простір називається фазовою площиною.

Фазова площина – це координатна площина, в якій по осях координат відкладаються дві змінні (фазові координати), які однозначно визначають стан системи другого порядку. Метод аналізу та синтезу системи управління, який базується на побудові фазового портрета, називається методом фазової площини.

Через будь-яку точку фазового простору може проходити лише одна траекторія. Однак, на фазовій площині існують особливі точки – точки в яких фазова швидкість рівна нулю, а отже це точки які є положенням рівноваги системи. Через особливі точки може проходити більше одної фазової траекторії.

Часто при зображенні процесів на фазовій площині за фазову координату , яку відкладають по осі ординат, приймають похідну координати , що відкладається по осі абсцис. В цьому випадку диференціальне рівняння фазових траекторій матиме вигляд:

.

Тоді фазові траекторії матимуть наступні властивості. У верхній півплощині зображуюча точка рухається зліва направо, оскільки та зростає. В нижній півплощині, навпаки, зображуюча точка рухається справа наліво так як та спадає. На осі абсцис ( ) похідна (за винятком точок рівноваги), і тому фазові траекторії перетинають вісь абсцис під прямим кутом.

Фазові портрети нелінійних систем характеризуються більшим різномаїттям, ніж фазові портрети лінійних систем. Однак типи особливих точок лінійних та нелінійних систем співпадають. Тут маються на увазі ті особливі точки, в околі яких рівняння нелінійних систем допускають лінеаризацію.

Фазові портрети та типи особливих точок лінійних систем. Нехай лінійна система другого порядку описується рівнянням

,

або в нормальній формі,

. (*)

Розв’язок, фазовий портрет та типи особливих точок залежать від коренів характеристичного рівняння

.

З рівняння (*) випливає, що система що розглядається має одну особливу точку в початку координат. В залежності від вигляду фазового портрету в околі особливих точок, останні поділяються на різні типи.

В табл. 1.2 наведені часові характеристики, фазові портрети та типи особливих точок при різних коренях характеристичного рівняння.

Таблиця 1.2

Тип коренів	Крива перехідного процесу	Фазовий портрет	Тип особливої точки
Чисто уявні			Центр
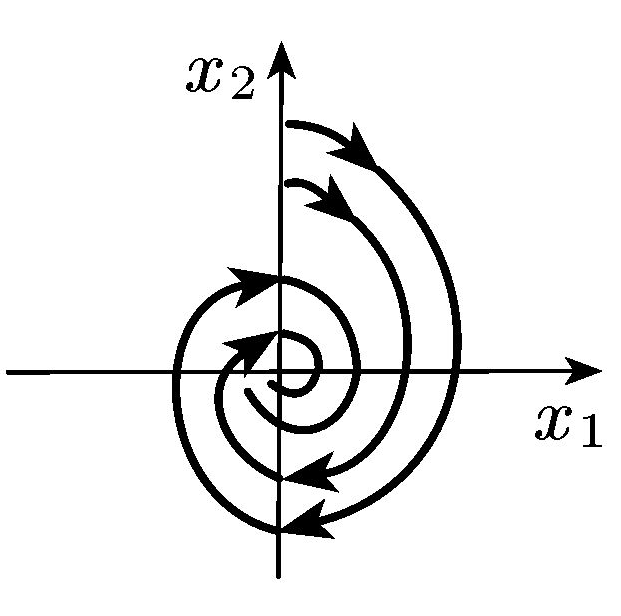
Комплексні з від’ємною дійсною частиною			Стійкий фокус
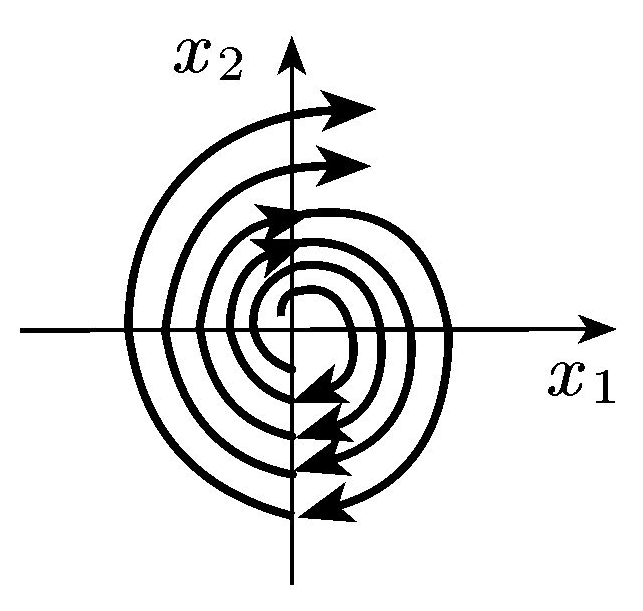
Комплексні з додатньою дійсною частиною			Нестійкий фокус
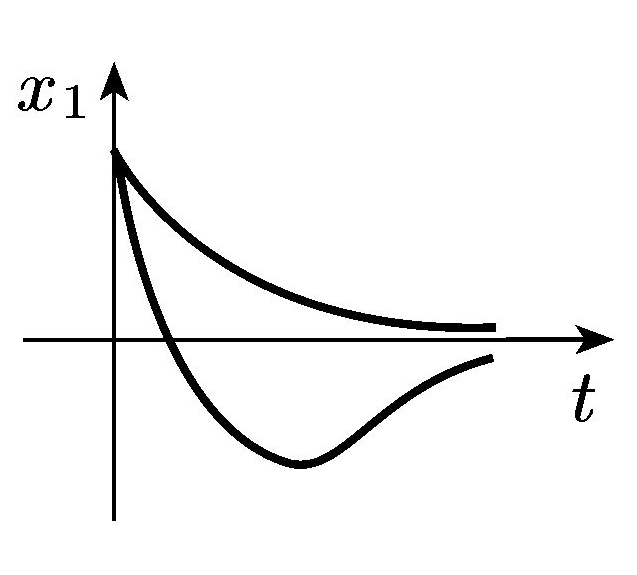
Дійсні від’ємні			Стійкий вузол
Дійсні додатні			Нестійкий вузол
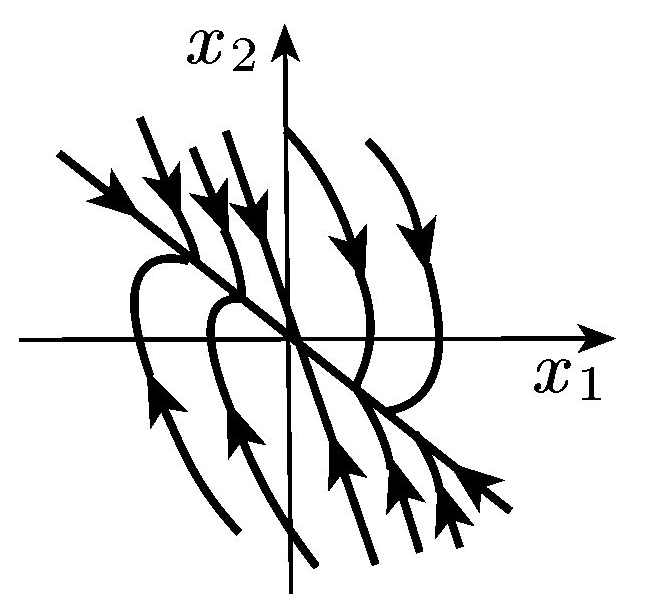
Дійсні різних знаків			Сідло

Коли корені характеристичного рівняння є чисто уявними,фазові траекторії є еліпсами або колами, тобто вони є замкнутими.

Замкнутим фазовим траекторіям відповідають незатухаючі коливання. Однак ці коливання не є автоколиваннями, так як їх амплітуда залежить від початкових умов і вони не є асимптотично орбітально стійкими.

Фазові портрети нелінійних систем. Нелінійні системи можуть мати декілька положень рівноваги (особливих точок) і характеризуються більшим різномаїттям фазових портретів. Якщо праві частини нелінійних рівнянь допускають лінеаризацію в околі особливих точок, то ці особливі точки можуть бути лише тих самих типів, що й особливі точки у випадку лінійних систем.

При наявності декількох точок рівноваги можливі різні типи фазових траекторій. Особливі криві, що розділяють фазову площину на області з різними типами фазових траекторій, називаються сепаратрисами.

Фазові портрети нелінійних систем можуть мати інший тип особливої кривої – ізольовані замкнуті траекторії. Ці криві називаються граничними циклами. Якщо зсередини та зовні фазові траекторії сходяться до граничного циклу (рис. 1.3*,а), то такий граничний цикл називається стійким граничним циклом. Стійкому граничному циклу відповідає асимптотично орбітально стійкий періодичний рух (автоколивання). В системі, у якої фазовий портрет має вигляд, представлений на рис. 1.3*,а, автоколивання виникають самовільно при будь-яких початкових умовах.

Рис. 1.3*. Граничні цикли

Якщо фазові траекторії зсередини та зовні граничного цикла віддаляються від нього (рис. 1.3*,б), такий граничний цикл називається нестійким граничним циклом. Періодичний процес що відповідає нестійкому граничному циклу неможливо спостерігати. Якщо рух починається всередині такого граничного цикла, то процес зходиться до положення рівноваги. Якщо рухпочинається зовні такого граничного циклу, то процес розходиться. Нестійкий граничний цикл є границею області притягання, або границею стійкості положення рівноваги (початку координат).

Можливі два граничні цикли (рис. 1.3*,в,г). Внутрішній граничний цикл на рис. 1.3*,в стійкий, і йому відповідають автоколивання, а зовнішній граничний цикл нестійкий і є границею області автоколивань: автоколивання виникають при будь-яких початкових відхиленнях, що не виходять за зовнішній граничний цикл.

Зовнішній граничний цикл на рис. 1.3*,г є стійким і відповідає автоколиванням, а внутрішній граничний цикл є нестійким і є границею області притягання положення рівноваги. В системі з таким фазовим портретом автоколивання виникають при досить значному відхиленні системи від положення рівноваги – відхиленні, яке виходить за межі внутрішнього граничного цикла. Якщо рух системи починається всередині нестійкого граничного цикла, то вона наближається до положення рівноваги.

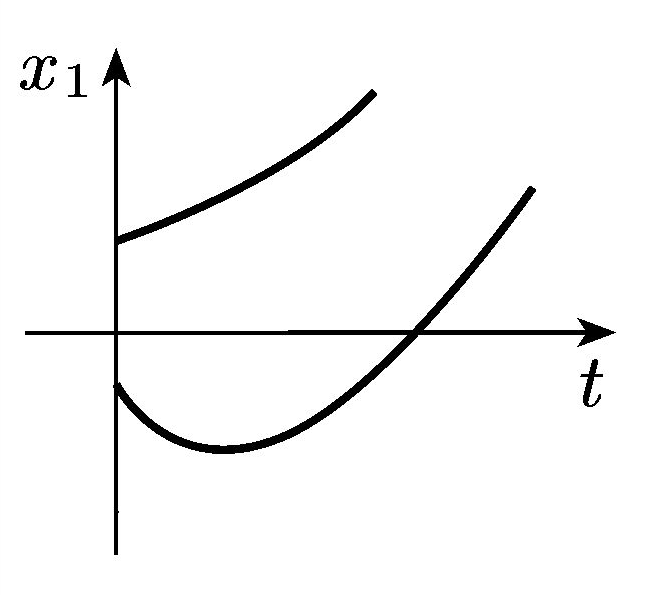
Побудова часових характеристик за фазовою траекторією

За фазовим портретом можна судити про характер перехідних процесів. Зокрема, по фазовій траекторії можна побудувати без розрахунків якісно часову характеристику – криву залежності від часу, і, навпаки, за часовою характеристикою можна побудувати фазову траекторію.

В якості прикладу спершу за фазовою траекторією побудуємо часову характеристику, а потім, за часовою характеристикою – фазову траекторію. Нехай задана фазова траекторія (рис. 1.4,а).

Рис. 1.4. Побудова часової характеристики за фазовою траекторією

Позначивши на ній характерні точки (початкову точку, точки перетину з осями координат), нанесем відповідні їм точки на часовій площині і з’єднаємо їх плавною кривою (рис. 1.4,б).

Рис. 1.5. До побудови фазової траекторії за часовою характеристикою

Нехай тепер задана часова характеристика (рис. 1.5,а). Позначивши на ній характерні точки (початкову точку, точки екстремума та точки перетину з віссю часу), нанесем відповідні їм точки на фазову площину і з’єднаємо плавною кривою (рис. 1.5,б).

Методи розрахунку та побудови фазових портретів

До основних методів розрахунку та побудови фазових портретів відносять: аналітичні; графічний наближений (метод ізоклін) та методи побудови за допомогою компьютерного моделювання.

Аналітичний метод.

Даний метод базується на розвязуванні диференціальних рівнянь руху системи.

Для початку необхідно отримати дифереціальні рівняння фазових траекторій, для чого нелінійне диференціальне рівняння системи другого порядку необхідно привести до нормальної форми Коші. Для цього спочатку диференціальне рівняння динаміки системи розв’язується відносно старшої похідної. Результат такого розв’язку можна записати у вигляді:

- загальний вигляд нелінійного диференціального рівняння, розв’язаного відносно старшої похідної,

де - регульована величина; - нелінійна функція.

Наприклад, маємо нелінійне рівняння другого порядку

Розв’язавши його відносно старшої похідної отримаємо

.

Для переходу до нормальної форми Коші здійснюємо підстановку

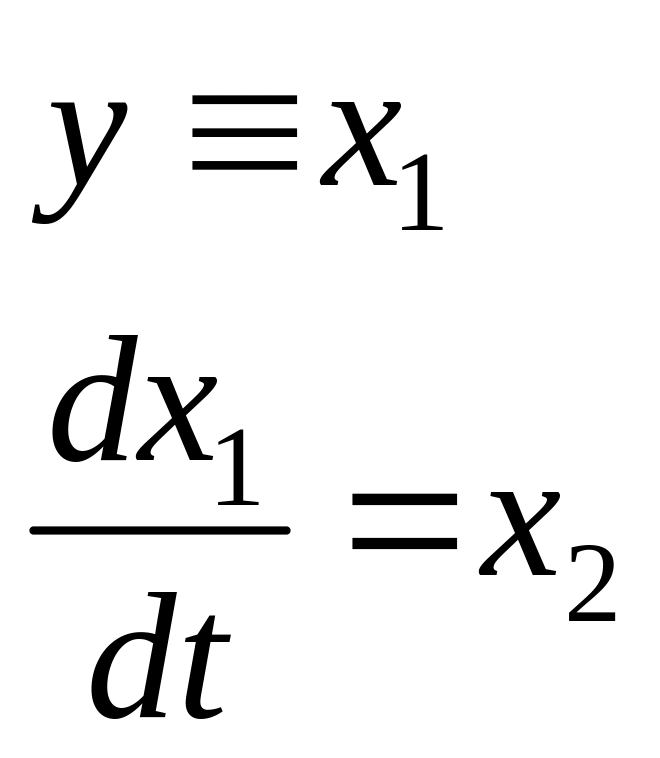
і отримаємо диференціальне рівняння системи у формі Коші:

Для отримання диференціального рівняння фазових траекторій, необхідно з диференціальних рівнянь у формі Коші виключити час. Цього можна досягти, поділивши перше диференціальне рівняння на друге. Отримаємо:

- диференціальне рівняння фазових траекторій.

Для побудови фазового портрету розв’язуємо диференціальне рівняння траекторій (розділяємо змінні та інтегруємо). Після чого проводимо побудову.

Якщо змінні у диференціальному рівнянні траекторій розділити не вдається, то використовують наближений метод побудови.

Метод ізоклін.

Ізокліною називається геометричне місце точок фазової площини, в яких фазові траєкторії мають однаковий нахил, тобто лінія, яку всі фазові траекторії перетинають під одним кутом. Із геометричного змісту похідної (тангенс кута нахилу дотичної до графіка функції) та диференціального рівняння фазових траекторій можна записати:

, /*/

де - нахил фазової траекторії на фазовій площині.

Отже у кожній точці фазової площини можна знайти цілком визначену величину нахилу фазової траекторії.

Спосіб побудови полягає у наступному. Із рівняння /*/ знаходимо функцію

, /**/

яка являє собою рівняння ізоклін.

Побудуємо ряд ізоклін 1-4 за рівнянням (**). У точці ізокліни 1 (рис. 1.6) проведемо дві прямі і з нахилами і відповідно до перетину з ізокліною 2. Отриманий на ній відрізок поділимо навпіл і через точку проведемо дві прямі і з нахилами і до перетину з ізокліною 3. Потім відрізок поділимо навпіл точкою , через яку проводимо прямі і з нахилами і і т.д. Через знайдені точки , , , … , проводимо фазову траєкторію. Точність побудови фазової траєкторії за методом ізоклін буде тим вища, чим частіше на графіку нанесені ізокліни.

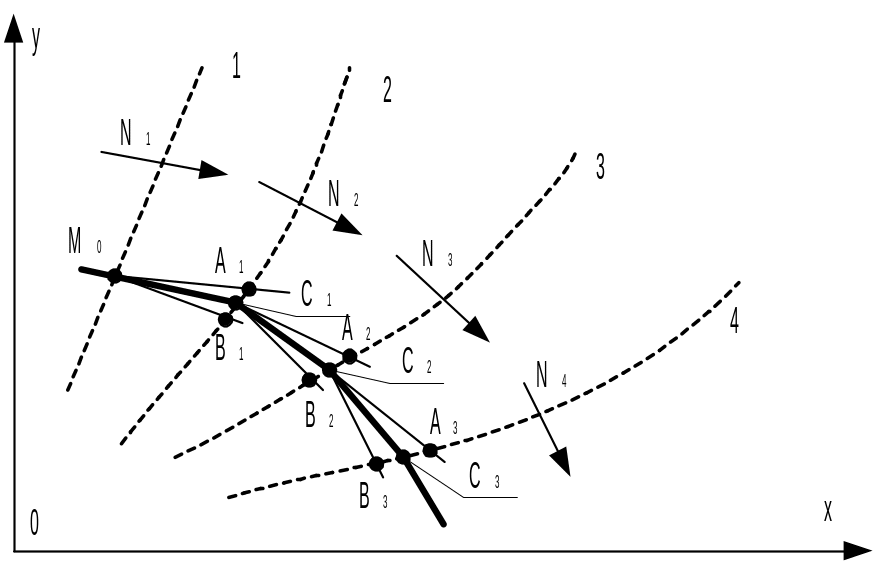
Рис. 1.6 - Побудова фазової траєкторії за методом ізоклін

Метод гармонічної лінеаризації

Метод гармонічної лінеаризації, або метод гармонічного балансу першочергово було розроблено для дослідження періодичних режимів. Однак з часом він став використовуватися для аналізу стійкості та синтезу нелінійних систем.

Основна ідея методу полягає в наступному. Керовані системи (об’єкти), як правило, мають властивості фільтра низьких частот: при виникненні періодичних режимів вони не пропускають або пропускають зі значним ослабленням другі та більш високі гармоніки. І суть методу гармонічної лінеаризації полягає в описі нелінійної ланки лінійним рівнянням, яке отримується при нехтуванні (відкиданні) вказаними гармоніками в розкладі нелінійної функції в ряд Фур’є.

Метод гармонічної лінеаризації є наближеним методом. Однак його перевагою є те, що його можна застосовувати до систем будь-якого порядку, на відміну від методу фазової площини.

Структурну схему замкнутої нелінійної системи, яка складається з нелінійної ланки та лінійної частини – лінійної ланки, будемо називати типовою структурною схемою нелінійної системи (рис.1.7).

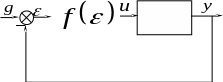
Рис1.7. Типова структурна схема нелінійної САУ

Розглядати будемо лише нелінійні системи, які представлені такою структурною схемою. Або які зводяться до неї.

Приймемо, що задаючий вплив . Рівняння системи мають вигляд:

, , . (+*)

Припустимо, що в системі виникає періодичний режим. Тоді нелінійна функція буде періодичною функцією часу, і її можна буде розкласти в ряд Фур’є:

,

де - коефіцієнти Фур’є; ; - період; трьома крапками позначені вищі (другі та більш високі) гармоніки.

Припустимо, що лінійна частина має властивості фільта низьких частот, тобто виконується умова

, ,

За цієї умови вищі гармоніки не здійснюють суттєвого впливу на вихідну величину лінійної частини. Тому при визначенні вищими гармоніками можна знехтувати, і рівняння системи (+*) представити у вигляді

, , . (+*+)

Якщо в системі виникає періодичний режим і лінійна частина є фільтром низьких частот, тобто справедлива гіпотеза фільтра, то коливання на виході лінійної частини і відповідно на вході нелінійної ланки є гармонічними.

Виберемо початок відліку так, щоб на вході нелінійної ланки . Тоді маємо

, .

Підставивши ці вирази в (+*+), при отримаємо

, , , (+**+)

де

,

,

або, якщо - однозначна нечітка функція,

, .

Система (+**+) при фіксованих амплітуді та частоті є лінійною. Перехід від вихідної системи (+*) до лінеаризованої системи (+**+) називається гармонічною лінеаризацією. Коефіцієнти та називають коефіцієнтами гармонічної лінеаризації. Передаточну функцію

називають передаточною функцією нелінійної ланки і відповідно вираз

,

який отримується при підстановці в передаточну функцію нелінійної ланки , називають частотною передаточною функцією нелінійної ланки. В останньому виразі коефіцієнти та являють собою дійсну та уявну частини. Тому будемо називати дійсним, а - уявним коефіцієнтом гармонічної лінеаризації.

Розрахунок коефіцієнтів гармонічної лінеаризації базується на побудові графіка вихідного сигналу нелінійної ланки, коли на її вхід подається гармонічний сигнал .

Коефіцієнти гармонічної лінеаризації типових нелінійностей неведено в таблиці

Таблиця

№
1			0
2			0
3
4			0
5			0

Дослідження параметрів автоколивань методом гармонічного балансу

При використанні методу гармонічної лінеаризації приймається, що гіпотеза фільтра виконується. Тоді, в системі виникає періодичний процес і на виході лінійної частини і на вході нелінійної ланки він є гармонічним . Тому періодичний режим однозначно визначається частотою та амплітудою , і дослідження періодичного процесу зводиться до визначення цих параметрів.

Основна умова виникнення періодичного процесу. В лінеаризованій системі можуть виникати гармонічні коливання, якщо її характеристичне рівняння має чисто уявні корені, або, якщо амплітудно-фазова характеристика розімкнутої системи проходить через точку , тобто якщо виконується рівність

. (-+)

Це співвідношення є рівнянням відносно невідомих параметрів, частоти та амплітуди і визначає основну умову виникнення періодичних процесів у системі що розглядається. Автоколивання в системі можливі якщо дане рівняння має дійсні додатні корені.

Є кілька методів дослідження автоколивань. Першим розглянемо аналітичний метод.

Підставивши в рівняння (-+) вирази для передаточних функцій лінійної та лінеаризованої частин, та позбувшись дробу, отримаємо рівняння у вигляді

,

або

(--++)

Якщо остання система рівнянь має розв’язок ( , ), то це означає, що гармонічно лінеаризоване рівняння має розв’язок яке описує періодичний процес.

Розв’язок описує автоколивання, якщо він асимптотично орбітально стійкий. Таким чином, дослідження автоколивань зводиться до розв’язку рівнянь (--++) та визначення асимптотичної орбітальної стійкості.

У випадку коли нелінійна ланка має однозначну характеристику і її передаточна функція має вигляд , асимптотичну орбітальну стійкість можна перевірити, скориставшись умовою, що коефіцієнт гармонічної лінеаризації повинен бути спадаючою функцією в околі точки , тобто повинна виконуватися нерівність

.

У випадку, коли нелінійна ланка має неоднозначну характеристику, для отримання умови асимптотичної орбітальної стійкості потрібно скористатися критерієм стійкості Михайлова. Основна умова виникнення періодичного процесу відповідає проходженню кривої Михайлова через початок координат. Умова асимптотичної орбітальної стійкості при неоднозначній характеристиці нелінійної ланки матиме вигляд

Зірочка при частинних похідних означає, що похідні визначаються в початку координат.

Графічний (частотний метод) дослідження автоколивань.

Рівняння , що визначає умову виникнення періодичного процесу, можна розв’язати графічно. Для цього представимо його наступним чином:

.

Будуємо амплітудно-фазову характеристику лінійної частини, тобто годограф функції , та обернену амплітудно-фазову характеристику нелінійної ланки з від’ємним знаком, тобто годограф функції . При побудові годографа змінюється частота, при побудові годографа змінюється амплітуда.

Якщо рівняння що розглядається має розв’язок, то вказані характеристики перетнуться. В точці перетину за годографом знаходимо частоту, а за годографом - амплітуду періодичного процесу.

Стійкість періодичного процесу встановлюється наступним чином. Якщо лінійна частина стійка, то періодичний процес буде асимптотично орбітально стійким, коли точка на годографі , що відповідає амплітуді знаходиться зліва від амплітудно-фазової частотної характеристики при русі по ній в сторону збільшення частоти.

Розглянутий графічний (частотний) метод був запропонований Л.С.Гольдфарбом та називається методом Гольдфарба.