
- •Зображення процесів на фазовій площині
- •Дослідження стійкості нелінійних систем
- •Величина
- •Величина
- •3. Дискретні та цифрові системи
- •3.1. Математичний апарат для дослідження імпульсних сак
- •3.2. Функціональна та алгоритмічна структури системи з амплітудно-імпульсною модуляцією
- •3.3 Передаточні функції імпульсної системи
- •3.4. Частотні характеристики імпульсних систем
- •3.5. Стійкість імпульсних систем
- •3.6. Якість імпульсних систем
- •3.7. Корекція імпульсних систем
- •3.8. Цифрові системи автоматичного керування
- •Дослідження цифрових систем автоматичного управління
- •Корекція цифрових систем
- •Синтез цифрових коректуючих пристроїв методом лачх
- •4. Одноконтурні та багатоконтурні системи
- •Комбіноване управління
- •Принцип інваріантності
- •7 Оптимальні системи автоматичного керування
- •10.1 Постановка й класифікація задач оптимізації
- •Обмеження фазових координат і керувань
- •Класифікація задач оптимізації
- •10.2 Класичні методи варіаційного числення
- •10.3 Метод динамічного програмування Беллмана
- •10.4 Принцип максимуму Понтрягіна
- •10.5 Аналітичне конструювання оптимальних регуляторів
- •11 Адаптивні системи автоматичного керування
- •11.1 Уявлення про адаптивні системи
- •11.2 Екстремальні системи керування
- •Системи екстремального керування крокового типу
- •Диференціальні системи екстремального керування
- •Градієнтом скалярної функції і(u1, u2, …, um) називається вектор з координатами тобто
- •Метод Гаусса-Зейделя (метод почергового змінювання параметрів)
- •11.3 Динаміка екстремальних систем
- •11.4 Самоналагоджувані системи керування
- •11.5 Ідентифікація об’єктів керування
Принцип інваріантності
Реалізація принципу інваріантності є ефективним засобом усунення протиріч між умовами точності в усталених та перехідних режимах шляхом компенсації зовнішніх збурень.
Термін інваріантність означає незалежність однієї фізичної величини від іншої. В системах управління розглядають незалежність вихідних величин від (керованої величини чи сигнала помилки) від вхідних впливів. В системах стабілізації прагнуть отримати незалежність керованої величини від збурюючих впливів, а в слідкуючих – незалежність сигнала помилки від задаючого впливу. В багатомірних системах з декількома контурами управління прагнуть незалежності кожної керованої величини від "чужих" керуючих впливів, які в контурі управління обраною величиною є збуреннями.
Система є інваріантною по відношенню до збурюючої дії, якщо після завершення перехідного процесу, який визначається початковими умовами, керована величина і похибка системи не залежать від цього впливу. Система є інваріантною відносно до задаючого впливу, якщо після завершення перехідного процесу, що визначається початковими умовами, похибка системи не залежить від цього впливу.
Багатомірні системи управління
До
багатомірних відносяться системи
управління, які мають кілька керованих
величин
![]() .
Це зустрічається в багатьох сучасних
складних системах. До них відносяться,
наприклад, системи стабілізації напруги
та частоти синхронних генераторів,
системи управління рухомих об’єктів,
багато систем управління технологічними
процесами та ін.
.
Це зустрічається в багатьох сучасних
складних системах. До них відносяться,
наприклад, системи стабілізації напруги
та частоти синхронних генераторів,
системи управління рухомих об’єктів,
багато систем управління технологічними
процесами та ін.
Багатомірна система передбачає наявність багатомірного об’єкта управління (рис. 4.3), який характеризується наявністю кількох входів (точок прикладання управляючих та збурюючих дій) та кількох виходів, які визначаються керованими величинами.
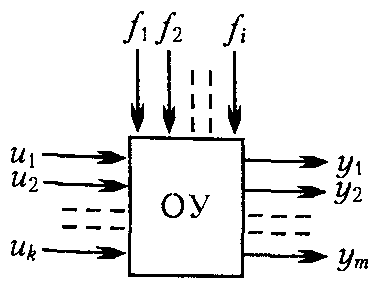
Рис. 4.3. Схема багатомірного об’єкта управління
Багатомірний об’єкт описується системою рівнянь, якку зручно представляти в матричній формі.
Введемо
![]() -мірну
матрицю-стовпець керованих величин
-мірну
матрицю-стовпець керованих величин
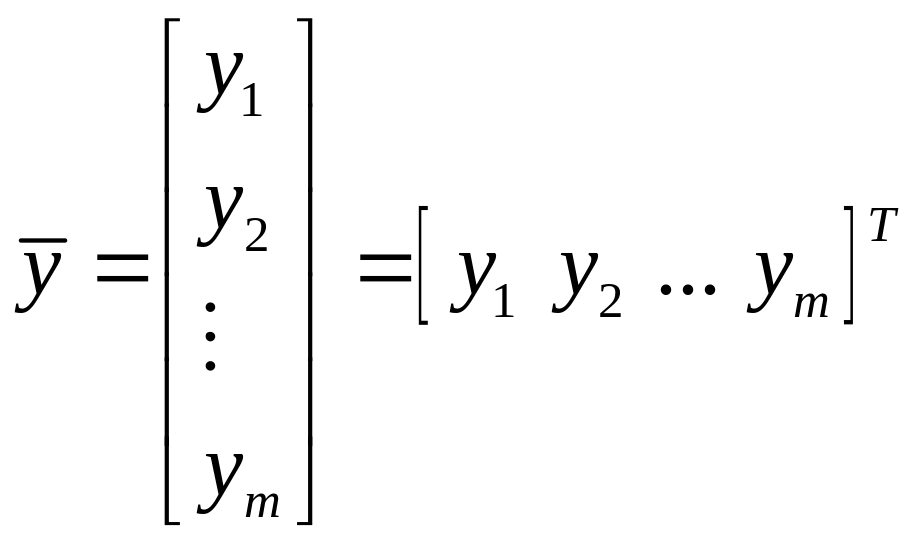 ,
(4.1)
,
(4.1)
-мірну матрицю-стовпець керуючих впливів
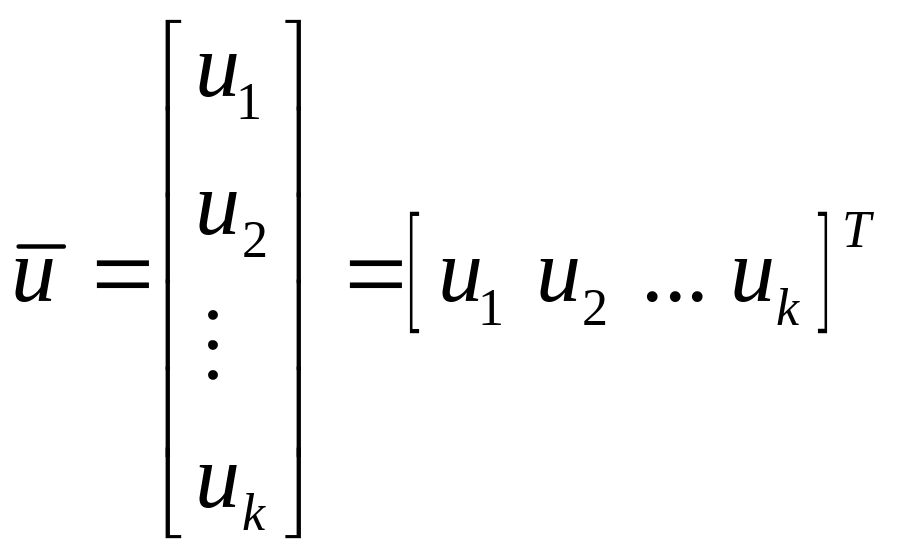 ,
(4.2)
,
(4.2)
та
![]() -мірну
матрицю-стовпець збурюючих впливів
-мірну
матрицю-стовпець збурюючих впливів
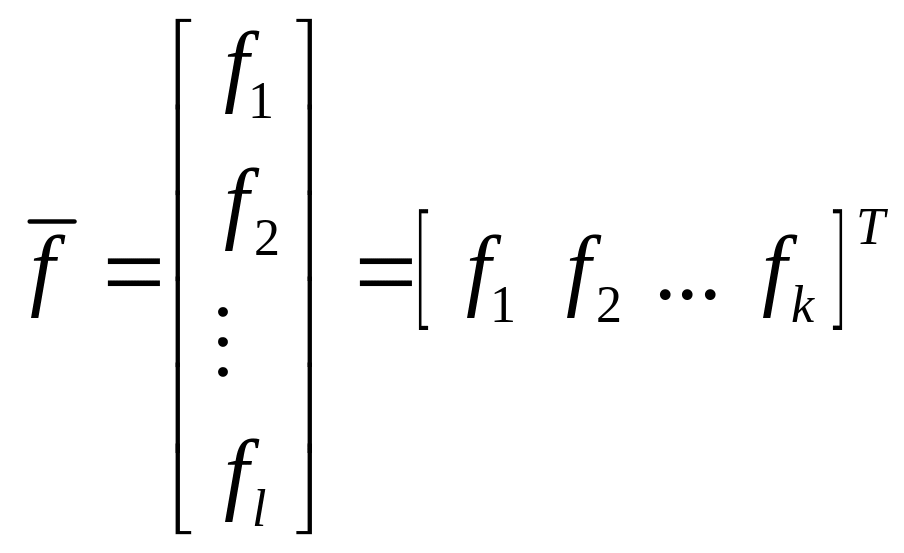 .
(4.3)
.
(4.3)
Тут індексом "Т" позначено операцію транспонування матриці.
Якщо керовані величини мають однакову фізичну розмірність і можуть трактуватися як проекції певного вектора на осі координат, то матриця-стовпець може бути тотожною цьому вектору. Тоді можна говорити про вектор керованих величин.
Якщо керовані величини мають різну фізичну розмірність, то перехід від матриці-стовпця до вектора можливий, якщо ввести в матрицю-стовпець вагові коефіцієнти, які б урівнювали розмірності окремих складових. Однак такий перехід не є єдиним і має безліч варіантів.
Аналогічно при рівності фізичних розмірностей окремих складових матриць-стовпців керуючих впливів та збурень можна ввести вектор управління та вектор збурень. При різних фізичних розмірностях окремих складових матриць-стовпців перехід до вектора можливий, але не буде єдиним.
Лінеаризовані рівняння руху багатомірного об’єкта можуть бути записані у матричному вигляді:
![]() .
(4.4)
.
(4.4)
Тут
введено квадратну матрицю операторних
коефіцієнтів розміром
![]()
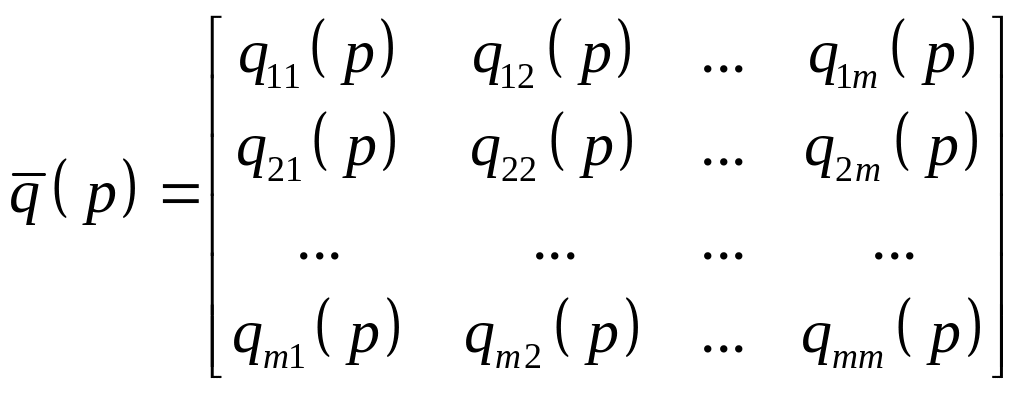 (4.5)
(4.5)
та
прямокутні матриці операторних
коефіцієнтів розміром
![]() та
та
![]()
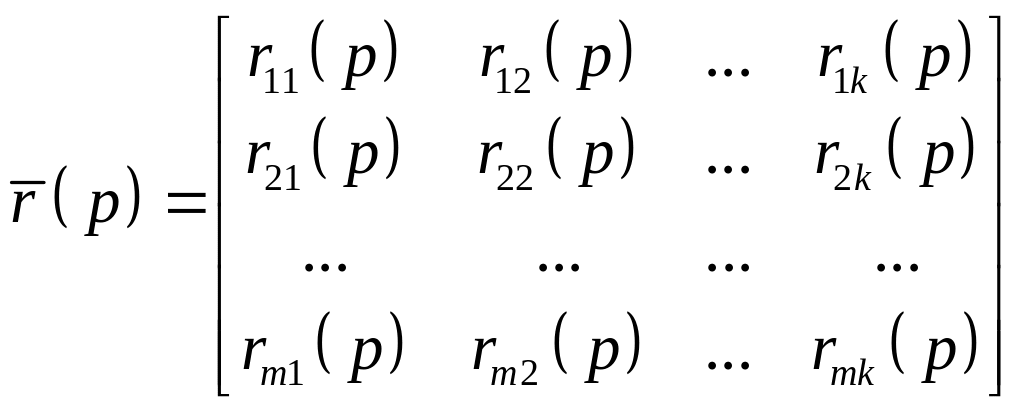 ;
(4.6)
;
(4.6)
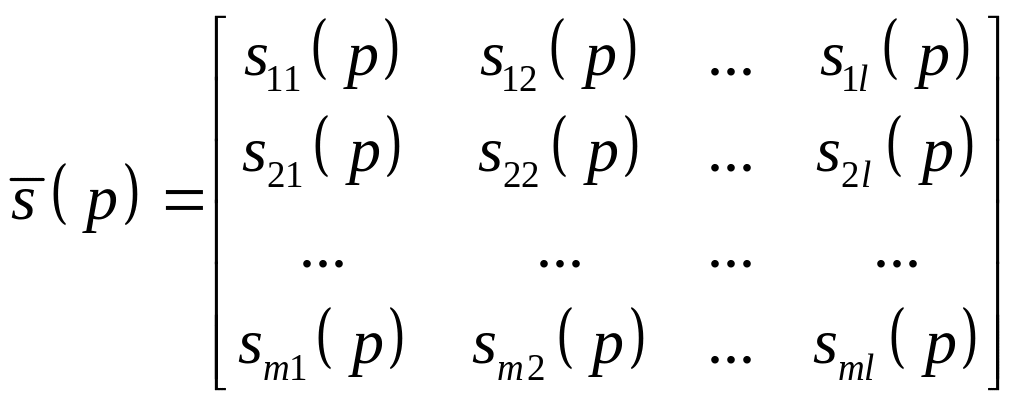 .
(4.7)
.
(4.7)
Якщо у виразах (4.1) – (4.7) перейти до зображень Лапласа при нульових початкових умовах, то матричне рівняння (4.4) можна записати для зображень в наступному вигляді:
![]() .
(4.8)
.
(4.8)
Тут
![]() ,
,
![]() та
та
![]() - матриці-стовпці зображень керованих
величин, керуючих впливів та збурень.
- матриці-стовпці зображень керованих
величин, керуючих впливів та збурень.
В
рівняння (4.8) входять також квадратна
матриця
![]() та прямокутні матриці
та прямокутні матриці
![]() та
та
![]() розмірами
,
та
відповідно.
розмірами
,
та
відповідно.
Якщо
матриця
не особлива, тобто її визначник не рівний
нулю, то, домноживши ліву і праву частини
(4.8) зліва на обернену матрицю
![]() отримаємо
отримаємо
![]() .
(4.9)
.
(4.9)
Тут введено матриці передаточних функцій об’єкта для керуючих впливів
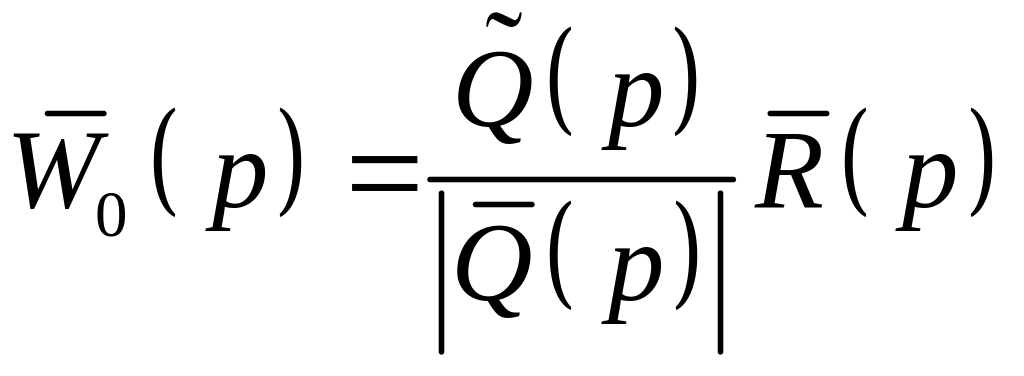 (4.10)
(4.10)
та для збурень
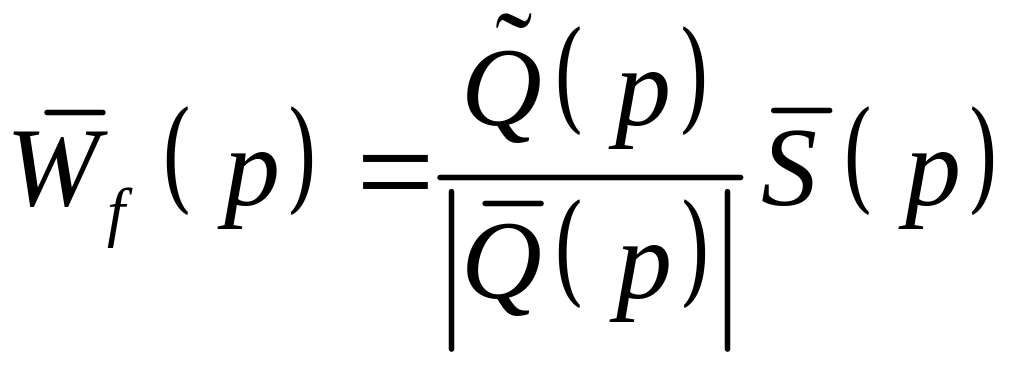 .
(4.11)
.
(4.11)
В
(4.11) символом
![]() позначено матрицю, приєднану для матриці
.
Формули (4.9) – (4.11) дозволяють отримати
зв’язок між керованими величинами та
керючими і збурюючими впливами.
позначено матрицю, приєднану для матриці
.
Формули (4.9) – (4.11) дозволяють отримати
зв’язок між керованими величинами та
керючими і збурюючими впливами.
На рис. 4.4. зображено умовну структурну схему замкнутої багатомірної системи.
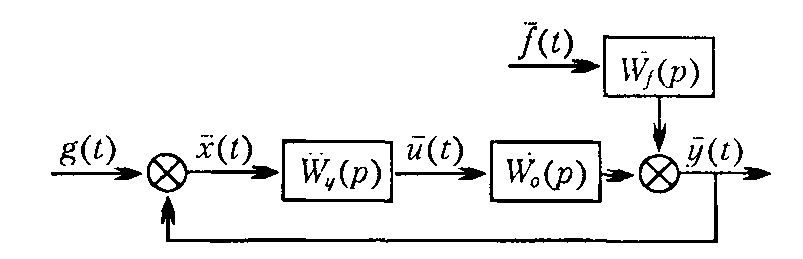
Рис. 4.4. Структурна схема замкнутої багатомірної системи
На
схемі всі вказані символи відповідають
матрицям:
![]() - задаючих впливів,
- задаючих впливів,
![]() - керованих величин,
- керованих величин,
![]() - похибок для кожної керованої величини,
- похибок для кожної керованої величини,
![]() - керуючих впливів,
- керуючих впливів,
![]() - збурень,
- збурень,
![]() - передаточних функцій для управління,
- передаточних функцій для управління,
![]() - передаточних функцій для збурень. Крім
того введено прямокутну матрицю
передаточних функцій керуючого пристрою
- передаточних функцій для збурень. Крім
того введено прямокутну матрицю
передаточних функцій керуючого пристрою
![]() ,
яка визначає алгоритми управління. Вона
дає зв’язок між зображеннями керуючих
впливів та похибок:
,
яка визначає алгоритми управління. Вона
дає зв’язок між зображеннями керуючих
впливів та похибок:
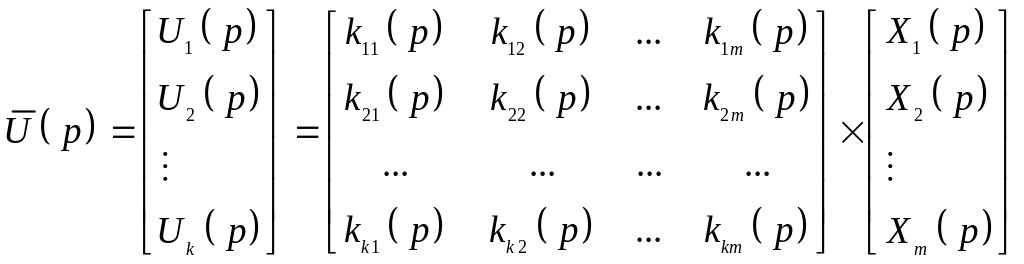 .
(4.12)
.
(4.12)
Рівняння багатомірної системи (рис. 4.4) можна отримати наступним чином.
Матриця передаточних функцій розімкнутої за всіма каналами системи
![]() .
(4.13)
.
(4.13)
Характеристична матриця системи являє собою квадратну матрицю розміром :
![]() .
(4.14)
.
(4.14)
Тут
![]() - одинична матриця розміром
,
тобто квадратна матриця, у якої всі
елементи головної діагоналі рівні
одиниці, а решта – нулю.
- одинична матриця розміром
,
тобто квадратна матриця, у якої всі
елементи головної діагоналі рівні
одиниці, а решта – нулю.
Характеристичне рівняння системи отримуємо, прирівнявши до нуля визначник характеристичної матриці:
![]() .
(4.15)
.
(4.15)
Зазначимо,
що у випадку, коли багатомірна система
є сукупністю
незалежних одномірних систем,
характеристична матриця буде діагональною
і визначник системи тоді рівний добутку
окремих визначників кожної з систем,
тобто
![]() .
В цьому випадку загальне характеристичне
рівняння розпадається на
незалежних характеристичних рівнянь
.
В цьому випадку загальне характеристичне
рівняння розпадається на
незалежних характеристичних рівнянь
![]() ,
,
![]() .
.
Матриці
передаточних функцій замкнутої системи,
за помилкою та за збуреннями, за умови,
що матриця
![]() не особлива, що означає незалежність
вихідних диференціальних рівнянь,
можуть бути визначені з виразів
не особлива, що означає незалежність
вихідних диференціальних рівнянь,
можуть бути визначені з виразів
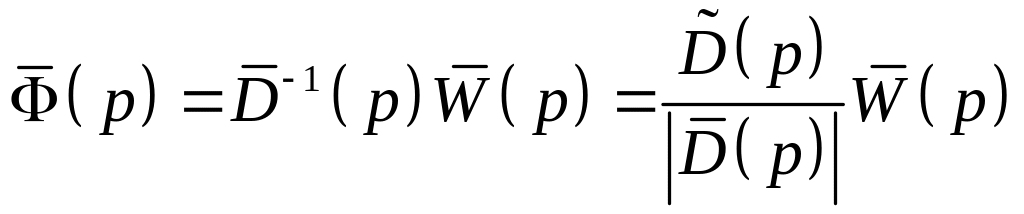 ,
(4.16)
,
(4.16)
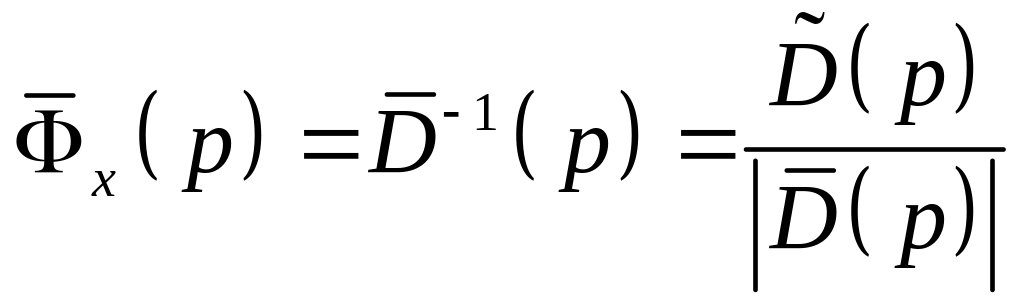 ,
(4.17)
,
(4.17)
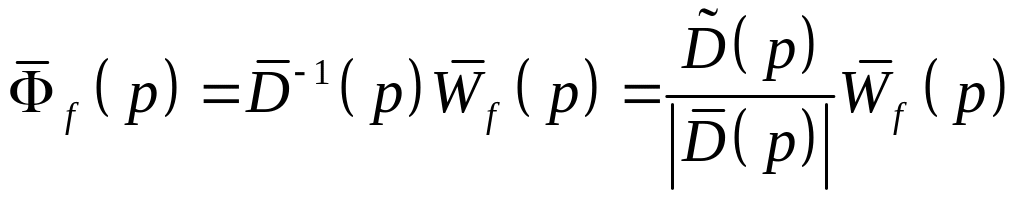 .
(4.18)
.
(4.18)
Тут
![]() - матриця, приєднана для матриці
.
- матриця, приєднана для матриці
.
