Розрахунок передаточних функцій імпульсних систем автоматичного регулювання
Мета заняття. Знаходження передаточних функцій імпульсних систем.
Задача 1. Знайти передаточну функцію розімкнутої імпульсної системи. Система складається з імпульсного елемента і неперервної частини.
Імпульсний елемент
здійснює амплітудно імпульсну модуляцію,
тобто виробляє прямокутні імпульси з
відносною тривалістю
.
Період слідування імпульсу 0,1с.
Неперервна частина – інерційна ланка
1-го порядку: к=1
і Т=1с.
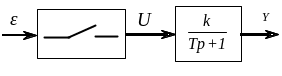
Рис. 4.1.
Розв’язок. Перетворимо структурну схему рис. 4.1. до вигляду рис. 4.2, в якій імпульсний елемент представлений двома ланками. Формуюча ланка є аналоговою ланкою.
Рис. 4.2.
При
Знайдемо передаточну функцію зведеної неперервної частини:
Рис. 4.3.
Передаточна функція
розімкнутої системи
.
На вході діє сигнал
на виході
Беремо дискретне зображення Лапласа
від решітчастої функції:
;
;
;
- z – зображення
;
Дискретна передаточна
функція тоді:
;
Передаточна функція імпульсної системи визначиться за наступною формулою:
;
.
Для визначення даного Z – зображення скористаємось таблицею 4.1 Z – зображень Лапласа.
Таблиця 4.1
X(t) |
X(nTi) |
L |
Z |
δ(t) |
δ(nTi) |
1 |
1 |
1(t) |
1(nTi) |
|
|
1·t |
nTi |
|
|
e-αt |
e-αnTi |
|
|
1-e-αt |
1-e-α nTi |
|
|
Згідно таблиці
;
де
;
тоді:
.
Завдання для самостійного виконання.
1.
Знайти
передаточну функцію розімкнутої
імпульсної системи. Система (рис. 4.4)
складається з імпульсного елемента і
неперервної частини. Параметри імпульсного
елемента:
,
Ті=
0,1с.
Неперервна частина – інерційна ланка
1-го порядку.
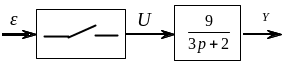
Рис. 4.4.
2.
Розв’язати
попередню задачу для наступних параметрів
імпульсного елемента:
,
Ті=
0,3с.
Неперервна частина – інерційна ланка
2-го порядку: к=10
і Т=0.1 с.
Рис. 4.5.
Практичне заняття №5.
Аналіз стійкості імпульсних систем
Мета заняття. Визначення стійкості імпульсних систем.
Задача №1. Визначити за критерієм Гурвіца стійкість системи, характеристичне рівняння якої має вигляд
25z3-5z2-10z-1=0.
Розв’язок.
Виконаємо
w – перетворення даного рівняння, тобто
виконаємо заміну
:
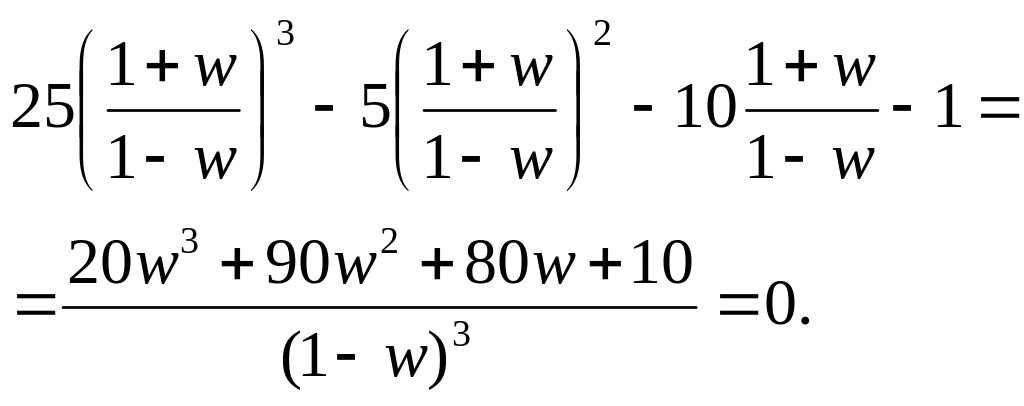
Перетворене характеристичне рівняння має вигляд:
Згідно з критерієм
Гурвіца система стійка, тому що
;
;
;
і
.
Завдання для самостійного виконання.
1. Характеристичне рівняння імпульсної системи регулювання
.
Визначити стійкість системи.
2. Визначити стійкість системи якщо характеристичне рівняння імпульсної системи регулювання має вигляд
.
3. Передаточна функція замкнутої імпульсної системи регулювання
Визначити стійкість системи.
Практичне заняття №6.