Міністерство освіти і науки, молоді та спорту України

Національний університет водного господарства та природокористування

Факультет прикладної математики і комп’ютерно-інтегрованих систем

Кафедра електротехніки та автоматики

Методичні вказівки

до проведення практичних занять з курсу

„Теорія автоматичного управління

Спеціальними системами”

Рівне – 2011

УДК 681.5

ББК 32.965

Теорія автоматичного управління спеціальними системами. Методичні вказівки до проведення практичних занять. – НУВГП, 2011.– с.

Розробник: А.О. Христюк, ст. викладач кафедри електротехніки і автоматики

Рецензенти: Баховець Б.О., професор, академік УЕАН,

М.І. Клепач, доцент каф. електротехніки і автоматики.

Затверджено на засіданні кафедри електротехніки і автоматики

Протокол № ___ від “_____”________________2011 р.

Зав.кафедрою _______________________Б.О. Баховець

Рекомендовано методичною комісією за напрямом підготовки „Автоматизація та комп’ютерно-інтегровані технології”

Протокол № ___ від “_____”________________2011 р.

Голова ____________________________ Б.О. Баховець

ББК 32.965

 НУВГП, 2011

Зміст

1. Розрахунок і побудова перехідних процесів в нелінійних системах методом припасовування

2. Розрахунок коефіцієнтів гармонічної лінеаризації нелінійних елементів

3. Розрахунок стійкості нелінійних систем. Визначення параметрів автоколивань

4. Розрахунок передаточних функцій імпульсних систем автоматичного регулювання

5. Аналіз стійкості імпульсних систем

6. Розрахунок перехідних характеристик та оцінка якості імпульсних систем

7. Розрахунок систем з ЕОМ у контурі керування

Практичне заняття №1.

Розрахунок і побудова перехідних процесів в нелінійних системах методом припасовування

Мета роботи: вивчити методику побудови математичної моделі нелінійної системи на основі її принципової схеми, ознайомитися з розрахунками і побудовою перехідних процесів в нелінійних системах методом припасовування.

До нелінійних систем не може бути застосований принцип суперпозиції. Порушення принципу суперпозиції в нелінійних системах не дає змоги використовувати відому реакцію системи на одноступінчасту дію для знаходження реакції системи на довільну вхідну дію. У зв’язку з цим дослідження нелінійних систем повинно проводитися багаторазово для всіх можливих діапазонів зміни вхідної величини.

Аналіз нелінійних систем ускладнюється ще й тим, що не існує єдиних математичних методів розв’язку нелінійних диференціальних рівнянь. Тепер розроблено велику кількість методів дослідження нелінійних систем, як точних, так і наближених. Найбільше поширення в теорії автоматичного керування отримали точні методи, що ґрунтуються на використанні фазового простору (фазової площини) і принципу припасовування. Серед наближених методів слід відзначити методи апроксимації і методи гармонічної та статистичної лінеаризації. Ефективним і універсальним методом дослідження нелінійних систем є моделювання процесів за допомогою ЕОМ.

Найпростішим методом аналізу нелінійних систем є метод припасовування. Суть методу полягає в тому, що розрахунок перехідної характеристики системи розбивають на ділянки, у відповідності з можливими станами релейного елемента. На межі ділянок діє принцип “зшивання”, при якому кінцеві значення зміни регульованої величини на попередньому інтервалі приймаються за початкові для розрахунку руху на наступному інтервалі.

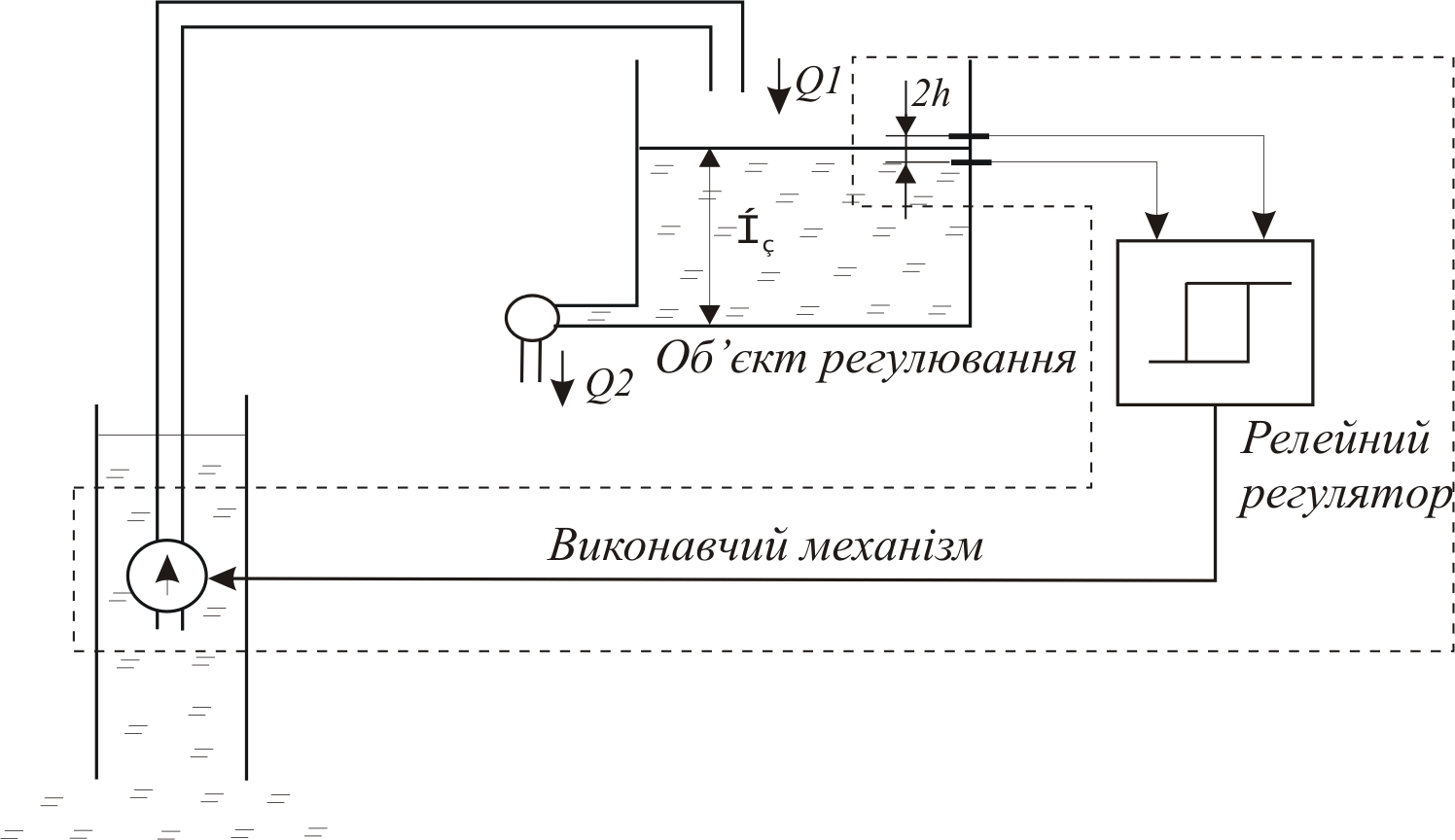
Задача №1. На основі наведеної схеми (рис. 1.1) нелінійної системи регулювання рівня рідини скласти математичну модель та побудувати перехідну характеристику. Схема складається з об’єкта регулювання і релейного регулятора. Н_с=1 м, h=0.1 м, k=0.01 c^-1.

Рис. 1.1. Нелінійна система автоматичного регулювання рівня рідини.

Розв’язок. Об’єктом регулювання є резервуар з постійною витратою рідини. Його динамічні властивості описуються передаточною функцією інтегруючої ланки

Об’єкт регулювання входить до лінійної частини нелінійної системи.

Релейний регулятор складається з давачів рівня, аналізуючого і підсилюючого пристрою, релейного елемента і помпи. Статична характеристика регулятора (рис. 1.2.) – кусочно-лінійна з зоною неоднозначності шириною 2h.

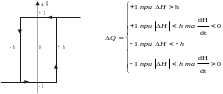
Рис. 1.2. Статична характеристика регулятора та її математичний опис.

На рис. 1.3. наведена структурна схема системи регулювання.

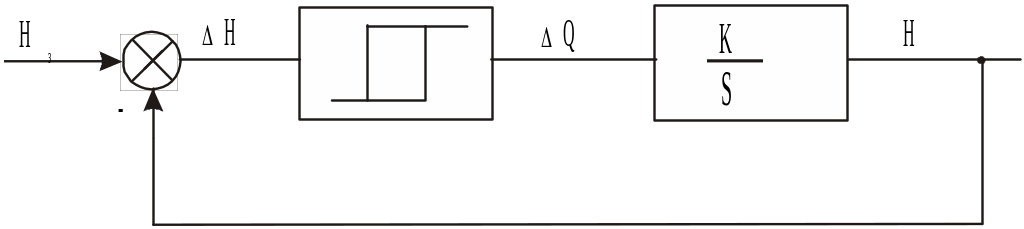
Рис. 1.3. Структурна схема системи.

Зі структурної схеми видно, що зображення регульованої величини H(p) зв’язано з зображенням регулюючої дії через передаточну функцію лінійної частини нелінійної системи

.

Звідси диференціальне рівняння об’єкта у операторній формі

.

Відповідно рівняння для оригіналів

.

Величина є нелінійною функцією , а отже, диференціальне рівняння

є також нелінійним.

Як слідує з рис. 1.2. характер нелінійності є такий, що у відповідності до того у якому стані знаходиться реле. Таким чином нелінійне рівняння може бути представлено у вигляді двох лінійних рівнянь, які відповідають включеному (1) і виключеному (2) станові реле

;

.

Розв’язок цих рівнянь дає змогу знаходити зміну регульованої величини у часі на окремих інтервалах часу, котрі відповідають різним станам реле. При цьому використовується метод “припасовування” або “зшивання” при якому кінцеві значення зміни регульованої величини на попередньому інтервалі приймаються за початкові для розрахунку руху на наступному інтервалі.

При після включення релейного регулятора рівень рідини буде змінюватися за законом

,

де - константа інтегрування, що визначається з початкових умов. У даному випадку початкові умови нульові , тому , а рівень рідини досягне заданої верхньої межі спрацювання 1.1 м , у момент часу :

c.

Після першого вимикання реле рівень рідини буде знижуватися. Закон зміни рівня на другому інтервалі знайдемо з розв’язку рівняння

Згідно з принципом припасовування початкові умови для другого інтервалу відповідають кінцевим значенням на першому інтервалі, тобто

м.

Тому .

У результаті зміна рівня на другому інтервалі

.

Другий інтервал закінчиться, коли рівень знизиться до відмітки 0.9 м, тобто в момент

с.

Далі побудову можна продовжувати аналогічним чином.

В результаті отримаємо наступну перехідну характеристику рис.1.4.

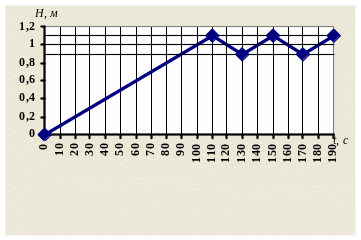
Рис. 1.4. Перехідна характеристика нелінійної АСР.

Завдання для самостійного виконання.

1. Визначити амплітуду і частоту автоколивань, наведеної на рисунку системи, якщо

1) k=1 c^-1, b=0.5, c=5,

2) k=1 c^-1, b=0.25, c=3,

3) k=2 c^-1, b=1, c=2,

4) k=3 c^-1, b=0.5, c=4,

5) k=2 c^-1, b=0.25, c=5.

2. Побудувати перехідну характеристику для системи, представленої структурною схемою, наведеною вище, якщо задано:

1) k=0,5 c^-1, b=1, c=5,

2) k=1,5 c^-1, b=2, c=2,

3) k=3 c^-1, b=0.5, c=3.

4) k=2,5 c^-1, b=3, c=2,

5) k=5 c^-1, b=2, c=1,

Практичне заняття №2.