5. Choice of excitation capacitor

Total reactive-power of capacitors Р_ex, required for excitation of three-phase asynchronous generator and compensation of phase-shift of loading,

Р_ex=Р_al∙(tg φ_G + tg φ), (42)

where Р_al − active-power, consumed by load (on three phases); φ_G, φ − angles of phase-shift between voltage and current of generator and load respectively.

As stated above, for generators of small power (up to 1 kW) a tgφ_G = 0,5÷0,7, and a power-factor of load usually is within the limits of 0,85÷0,95, i.е. tgφ = 0,3÷0,6.

Thus, necessary power of excitation capacitors is approximately equal to the consumable active-power, i.е.

Р_ex ≈ Р_al (43)

Because power of excitation

Р_ex = 2π∙f∙С_cb∙U_c², (44) I" (4.44)

then the capacity of capacitors block diminishes with the increase of frequency and voltage at a capacitor:

С_cb=Р_ex / (2πfU_c²) (45) : (4.45)

However with the increase of operating voltage a mass of capacitors increases, and with the increase of frequency it is necessary to reduce operating voltage because of internal losses growth in capacitor.

For the capacitors of type К75-10, being the best for operating in the alternating current circuits, dependence of mass М_C of operating voltage

М_C≡k_cU_op²С_cb (46)

where k_c − coefficient of proportionality, g/(V²F).

The value of k_c depends on mass of capacitor and is span:

k_c =(0,8÷1,2)∙10³.

D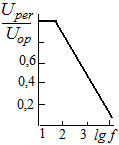 ependence of permissible voltage U_per at the capacitor is determined by technical requirements. For capacitors К75-10 this dependence can be presented by expression:

^{Uper / Uop = 1,9÷0,45lg f (47)}

The graphic image of this dependence is presented on a fig. 10.

Fig. 10 From(47) it is possible to find expressions for specific mass of capacitors

М_с/Р_ex = (k_с/2π)1/[f (1,9÷0,45lg f)]. (48)

The graphic image of dependence of capacitor specific mass on frequency is presented on a fig. 11. The got result (48) shows that specific mass of capacitors does not depend on voltage and is minimum on frequency 2400 Hz. A circuit of capacitors connection does not import also: a star or triangle − mass of capacitors is identical. It is important only, that capacitors were used at their voltage rating.

I f a generator operates at environment temperature below 70°C, a voltage at capacitor can be increased on 20%, here specific mass of capacitors diminishes yet on 40%.

At star connection of capacitors, when voltage at capacitor equals to phase one U_с Fig. 11 = U_ph1 a capacity of capacitors on a phase is

С_λ = [1/(2π∙f∙U_ph1²)]∙Р_ex/3. (49)

If capacitors are connected in a triangle, then voltage at them increases in √3 times as compared to voltage at connection of capacitors in a star, and a capacity diminishes in three times

C_Δ ={1/[2π∙f∙ (√3∙U_ph1)²]}∙P_ex/3. (50)

For the optimal use of capasitors at their triangle connection it is necessary to choose them on heightened operating voltage, not to exceed the permissible specific losses and field intensity in the dielectric of capacitor.

At the known design parameters of generator and given voltage and frequency a capacity of capacitors at their star connection equals to:

С_Y = 1/(ω₁²∙L₁) = 1/ [ω₁²(X₁ + X_m0) / ω₁] = 1/ [ω₁(X₁ + X_m0)], (51) where X_m0 = Е_phо/I_mо − inductive resistance of magnetizing contour at o.c. of generator (point A on a fig. 1).