14. Расчет рамок съемочных трапеций
Полученные ранее формулы позволяют легко вывести выражения для размеров рамок съемочных трапеций.
1. Пусть на рис. 14.1 изображена съемочная трапеция масштаба 1: n; широта южной параллели B1, северной — B2, разность долгот западного и восточного граничных меридианов трапеции Δl.
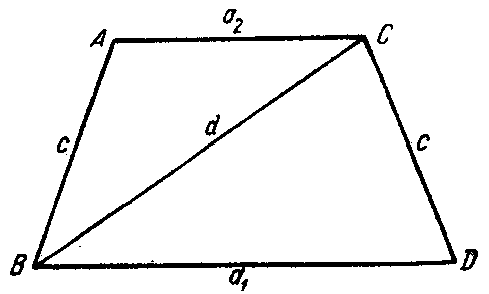
Рис. 16.1
Очевидно, западные и восточные рамки трапеции равны и представляют собой дуги меридианов между параллелями с широтами B1 и B2. Поэтому
,
(16.1)
где
ΔB = B2 – B1.
Северная и южная рамки являются дугами параллелей, имеющих соответственно широты B2 и B1, поэтому
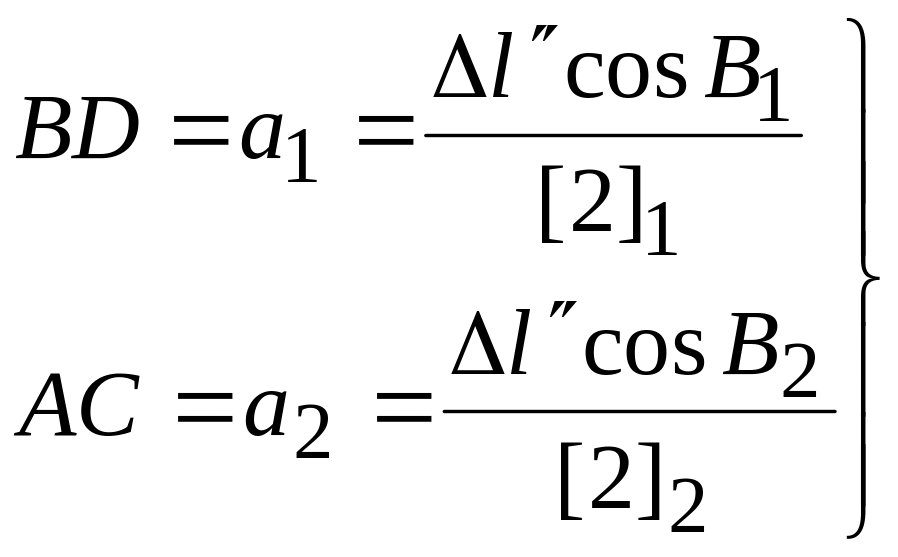(16.2)
Для получения размеров рамок в заданном масштабе необходимо найденные величины разделить на знаменатель масштаба, а для получения размеров сторон трапеции в сантиметрах умножить на 100.
Поэтому окончательно будем иметь:
.
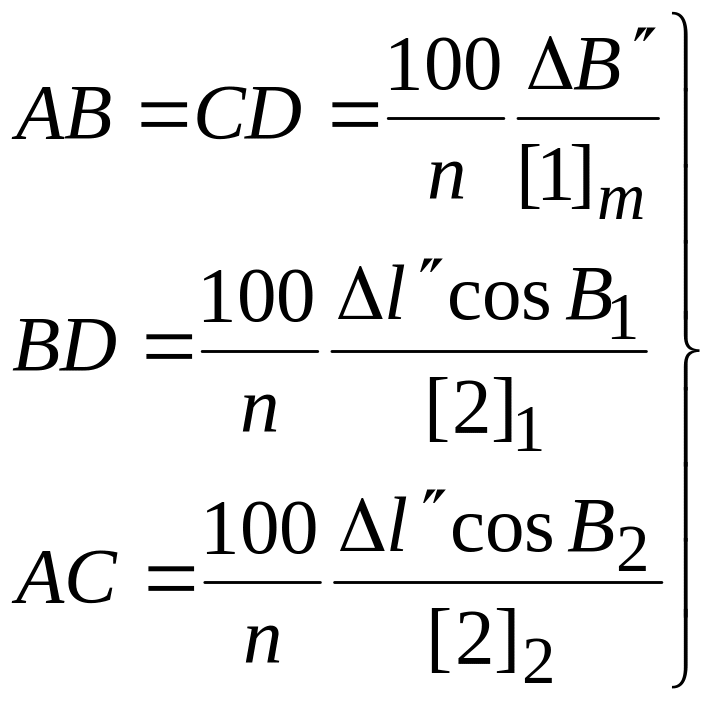(16.3)
Вычисление длин рамок по полученным формулам не представляет затруднений и ведется применительно к схемам, примеров.
Обычно, практически размеры рамок трапеций выбираются из специально составленных таблиц. В настоящее время такими таблицами являются «Таблицы координат Гаусса — Крюгера и таблицы размеров рамок и площадей трапеций топографических съемок», 'М., 1947) и «Таблицы для построения рамок трапеций топографических съемок масштабов 1: 5000 и 1: 2000»
17. Соотношение между длиной дуги нормального сечения на эллипсоиде и длиной дуги окружности
Возьмем на эллипсоиде точку А (рис. 17.1), имеющую широту В1.
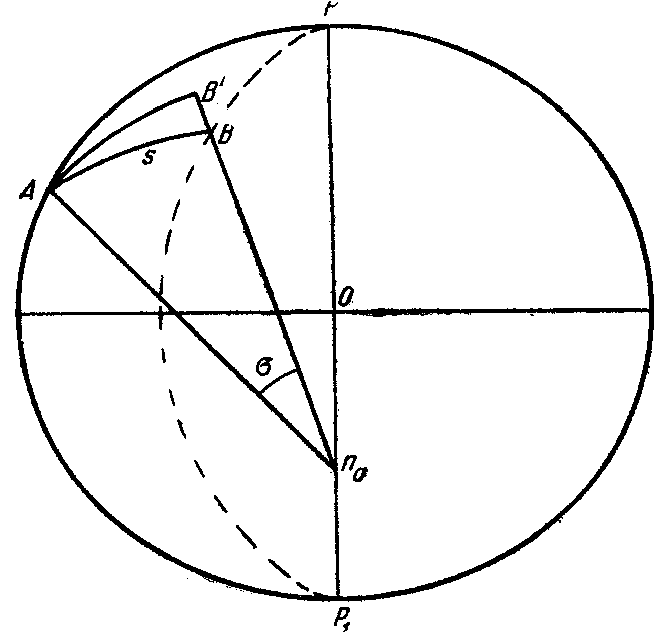
Рис. 17.1
Пусть na— пересечение нормали в точке А с малой осью эллипсоида PP1. Возьмем на поверхности эллипсоида вторую точку В, которую соединим с точкой na, Ana будет являться радиусом кривизны первого вертикала N1 в точке А. Опишем в плоскости АВna окружность радиусом N1 из na как из центра. Обозначим через В' точку пересечения нашей окружности с продолжением прямой naВ.
Назовем длину дуги нормального сечения АВ через s; соответствующая ей длина дуги окружности АВ' будет измеряться углом σ.
Соотношение между длиной дуги нормального сечения s и длиной дуги окружности выражается следующей формулой, которую приводим без вывода:
.
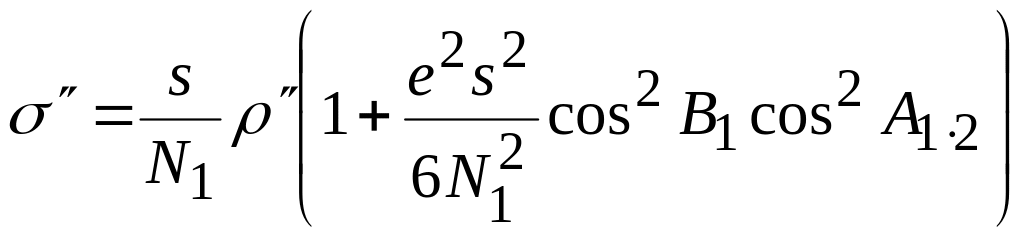(17.1)
где А1·2 – азимут нормального сечения из A в B, или
.
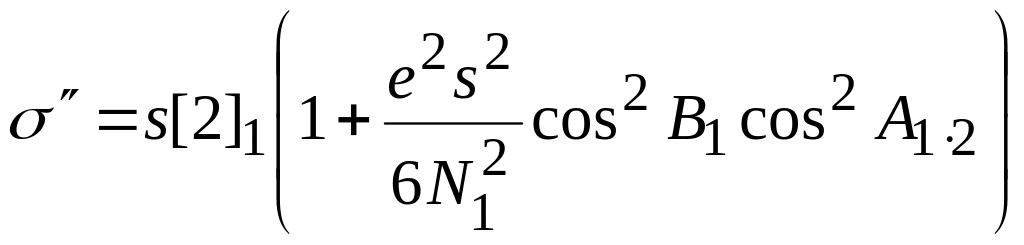(17.2)
Эта формула при s = 150 км точна до 0",0001; при s ≤ 40 км поправочным членом можно пренебречь, тогда будем иметь
σ" =[2]1 s. (17.3)
Соотношения (17.2) и (17.3) будут необходимы при выводе ряда следующих формул.