12. Вычисление длины дуги параллели

Параллель на эллипсоиде вращения является окружностью, поэтому вычисление дуги параллели сводится к определению дуги окружности с центральным углом, равным разности долгот конечных точек дуги.

Радиус параллели r определяется по формуле (9.9), которая имеет вид:

. (12.1)

Длина дуги параллели s΄, имеющей широту В и разность долгот конечных точек дуги l, очевидно, дается формулой:

. (12.2)

Отсюда легко получаем разность долгот двух точек параллели под широтой В, расположенных на расстоянии s',

l" = [2]s' sec B (12.3)

В табл. 3 приводятся для справок длины дуг параллелей для широт от 30 до 70° на эллипсоиде Красовского.

Таблица 3

В	Длина дуги параллели (м)
	в один градус	в одну минуту	в одну секунду
30° 40° 50° 60° 70°	96 489,9 85 395,3 71 696,9 55 800,9 38 187,2	1608,1 1423,3 1194,9 930,0 636,5	26,8 23,7 19,9 15,5 10,6

П р и м е р. Вычислить длину дуги параллели между точками, лежащими на одной параллели, если даны долготы этих точек и широта параллели.

L₂ = 64°53'17",358 L₁ = 62°45'14",812 B = 55°48'12",382

L2 L1 l = L2 - L1 l"

64°53'17",358 lg l" 62°45'14",812 lg cosB 2°08'02",546 доп lg[2] 7682",546 lg s s

3.8855 0517 9.7497 6238 1.4912 7268 5.1265 4023 133 825,912 м

13. Вычисление площадей съемочных трапеций

Вычисление площади съемочной трапеции или листа карты сводится к определению части поверхности эллипсоида, ограниченной линиями меридианов и параллелей.

Возьмем на эллипсоиде (рис. 13.1) два бесконечно близко расположенных меридиана РВАР₁ и PCDP₁ с долготами l и 1 + dl и две бесконечно близко расположенные параллели TBCR и QADS с широтами В и B+dB, пересечения которых образуют бесконечно малую трапецию АВСD.

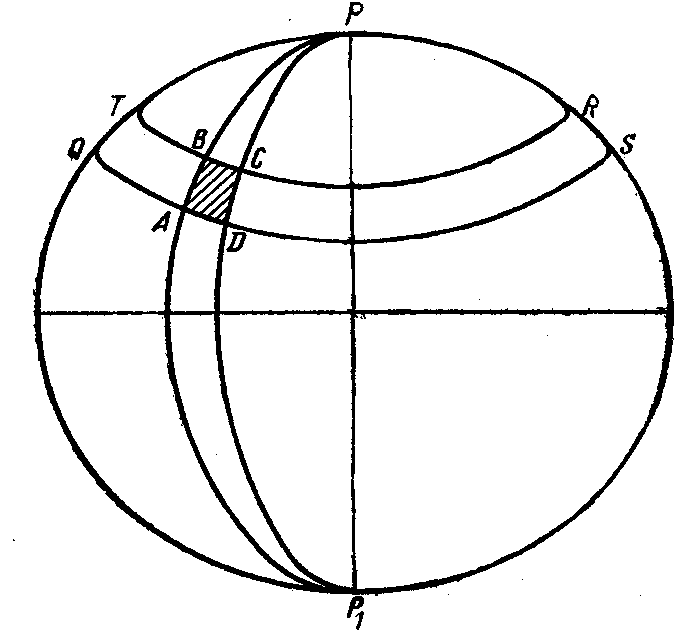
Рис. 13.1

Стороны этой трапеции как элементы дуг меридианов и параллелей будут равны:

AB= CD = М dB,

AD = ВС = NcosBdl.

Площадь элементарной трапеции ABCD выразится формулой:

dТ = MNcos BdB dl. (13.1)

Площадь dZ всего пояса, ограниченного указанными параллелями, получится, если в формуле для dT величину dl заменить через 2π, т. е

dZ = 2π MN cos BdB = 2π R² cos BdB,

или

. (13.2)

Площадь поверхности пояса эллипсоида, расположенного между параллелями с широтами B₁ и В₂, будет:

. (13.3)

Для вычисления интеграла (13.3) разложим подинтегральную функцию в ряд по биному Ньютона (интеграл берется и в конечном виде, однако получаемое при этом выражение мало пригодно для вычислений):

(13.5)

Для приведения этой формулы к виду, удобному для практического применения, воспользуемся формулами, дающими выражения синусов нечетных степеней в функции синусов кратных дуг(эти формулы получаются на основе общей формулы:

(13.6)

Заменяя в формуле (13.5) синусы нечетных степеней согласно выражениям (13.6) и подставляя пределы интегрирования, будем иметь:

(13.7)

Заменяя разности синусов по известным формулам тригонометрии, получим:

При разложении выражения (13.4) в ряд члены с е⁶, е⁸ и т. д. не были приняты во внимание. Более точная формула для площади пояса, с учетом членов с е⁶, е⁸, будет иметь следующий вид:

Для эллипсоида Красовского эти коэффициенты имеют следующие численные значения:

1g А' = 0.001 45834

1g В' = 7.050 7767_-10

1g C' =4.230 14_-10

1g D' = 1.428_-10

(13.9)

Формула (13.8) выражает площадь пояса эллипсоида, ограниченного параллелями с широтами В₁ и В₂. Чтобы получить формулы для вычисления площадей трапеций данного масштаба и номенклатуры, берут разность широт северной и южной рамок трапеций B₂ — B₁ и определяют, какую долю площади всего пояса составляет площадь трапеции данного масштаба, причем, очевидно, эта доля определится в зависимости от разности долгот меридианов западной и восточной рамок трапеции.

Например, для государственной карты масштаба 1: 1 000 000 B₂ — B₁ = 4°; разность долгот восточной и западной рамок карты Δl = 6°, т. е. равна 1: 60 от полной окружности пояса. Поэтому рабочая формула для вычисления площадей трапеции масштаба 1: 1 000 000 будет:

(13.10)

Положив в формуле (13.7) B₁ = 0, B₂ = 90° и удвоив полученное выражение, получим формулу для вычисления площади ∑ всей поверхности эллипсоида с удержанием любого числа членов, так как закон построения членов ряда совершенно ясен:

(13.11)

Рассмотрим пример на вычисление площади трапеции масштаба 1: 100 000.

П р и м е р. Вычислить площадь трапеции карты масштаба 1:100 000 N-36-14.

Для площади трапеции карты этого масштаба формула будет иметь следующий вид:

Имеем:

B₂ = 55°40΄; В₁ = 55°20΄; В_m = 55°30΄.

Вычисления производим по следующей схеме:

1g А' lg sin 10° lg cos Вm lg I I

4583 7.463 7255-10 9.753 1280-10 7.218 3118-10 +0,001 653148

1g B' lg sin 30° lg cos 3Вm lg II II

7.05 078-10 7.94 084-10 9.98 783n -10 4.97 945n -10 -0,000009538

1g C' lg sin 50° lg cos 5Вm lg III III

4.23-10 8.16-10 9.12-10 1.51-10 +0,00000003

I -II +III k	+0,001653148 +0,000009538 +0,000000003	lg π 2 lg b доп. lg 180	0.497 1499 7.606 4857 7.744 7275-10	lg Q lg k	5.848 3631 7.220 8110-10
	+0,001662689	lg Q	5.848 3631	Lg P	3.069 1741

Р = 1172,666 кв. км.