17

Тема №1 основные формулы и соотношения на поверхности земного эллипсоида (л№3)

10. Главные радиусы кривизны в данной точке эллипсоида

Вспомним, что через нормаль к поверхности эллипсоида можно провести бесчисленное множество плоскостей. Эти плоскости, перпендикулярные касательной плоскости к поверхности эллипсоида в данной точке, называются нормальными. Кривые, образуемые от пересечения нормальных плоскостей, проведенных в данной точке, с поверхностью эллипсоида, называются нормальными сечениями.

В каждой точке существует два взаимно перпендикулярных нормальных сечения, кривизна которых имеет максимальное и минимальное значение; эти нормальные сечения называются главными нормальными сечениями.

В некоторой точке М на поверхности эллипсоида вращения главными нормальными сечениями, как известно, будут:

1) меридианное сечение — сечение, проходящее через данную точку М и оба полюса эллипсоида Р и. Р₁. (На рис. 10.1 меридианное сечение в точке М представляется эллипсом РМЕ₁Р₁Е);

2) сечение первого вертикала — сечение, проходящее через точку М и перпендикулярное к меридианному сечению точки М. (Сечение первого вертикала изображено на рис. 10.1 кривой WME, представляющей собой также эллипс).

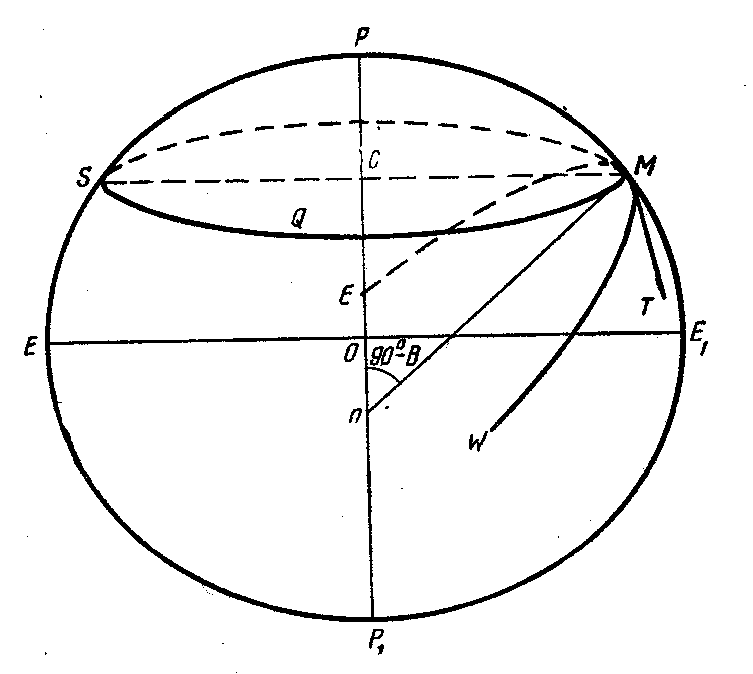
Рис. 10.1

Обозначим через М и N радиусы кривизны меридиана и первого вертикала соответственно. Найдем выражения для радиусов кривизны главных нормальных сечений в функции геодезической широты В, большой полуоси а и эксцентриситета е. Радиус кривизны R плоской кривой, выражаемой уравнением вида y=f(x), определяется формулой:

.

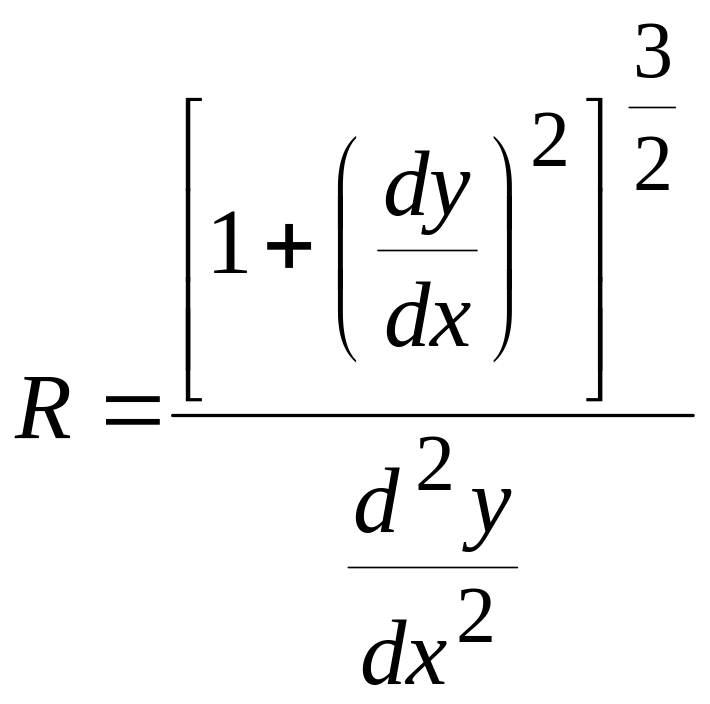Применяя эту формулу к меридианному эллипсу, напишем:

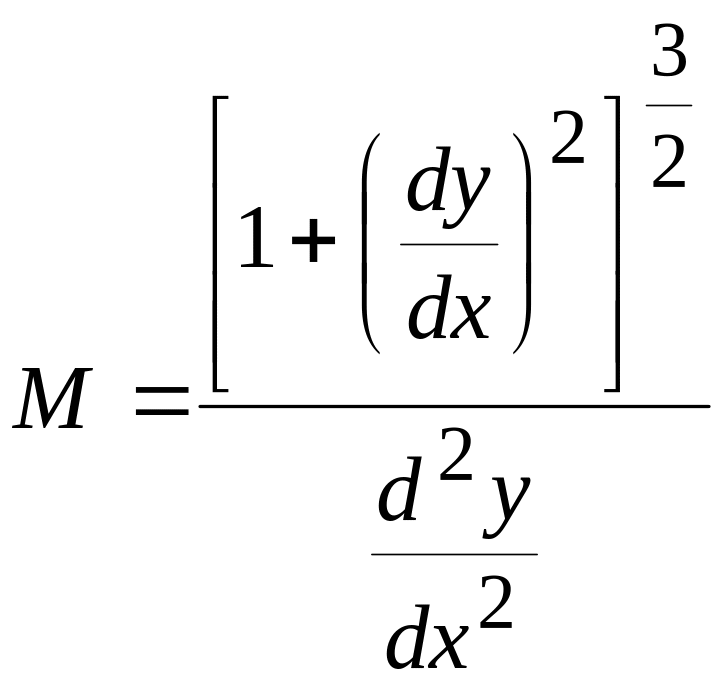. (10.1)

Применив эту формулу к эллипсу, имеющему уравнение

.

Вспомним, что сопоставляя выражения производной через геодезическую широту и прямоугольные координаты х, у, на основании (9.2) и (9.3) получили формулу (9.4):

. (9.4)

Выразив в (10.1) величину согласно (9.4) и с учетом ; (лекц №1, ф-ла 1.7), дифференцируя 2-й раз получим для радиуса кривизны М меридиана

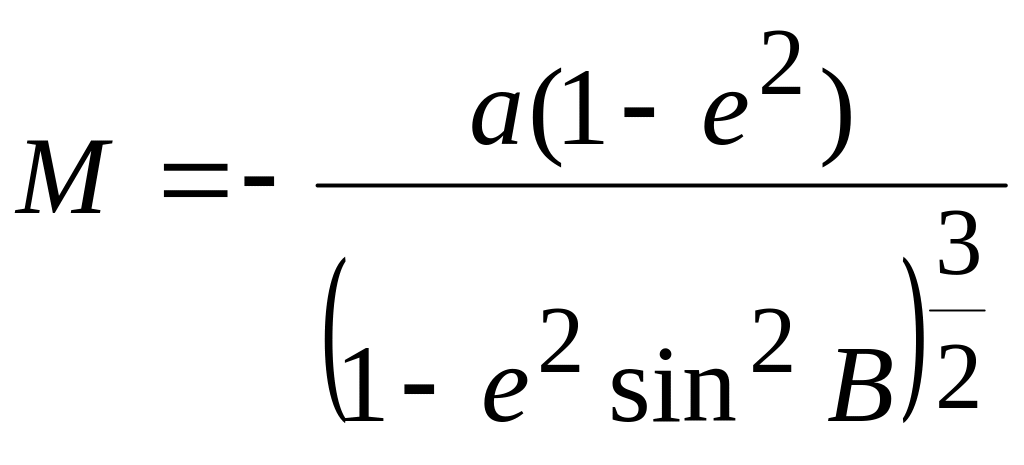. (10.2)

Знак минус показывает направление вогнутости кривой относительно оси абсцисс. Нас интересует только длина радиуса кривизны, а при ее определении знак минус, конечно, во внимание не принимается.

Радиус кривизны первого вертикала обозначаемый через N, определяется формулой (напишем эту формулу без вывода)

. (10.3)

Составив на основании формул (10.2) и (10.3) отношение , легко видеть, что при В = 90° это отношение равно 1, т.е. =1, а при других значениях широты В оно всегда больше 1. Поэтому можно сказать, что на полюсах М = N, а во всех других точках на поверхности эллипсоида N> М.

Для практических вычислений обычно используют величины , которые обозначают символами [1] и [2] соответственно, т.е.

=[1] и =[2]. (10.4)

Логарифмы этих величин выбираются из специальных геодезических таблиц по аргументу широты.

В прямоугольном треугольнике NCT (см. рис. 10.2) гипотенуза определяется формулой

.

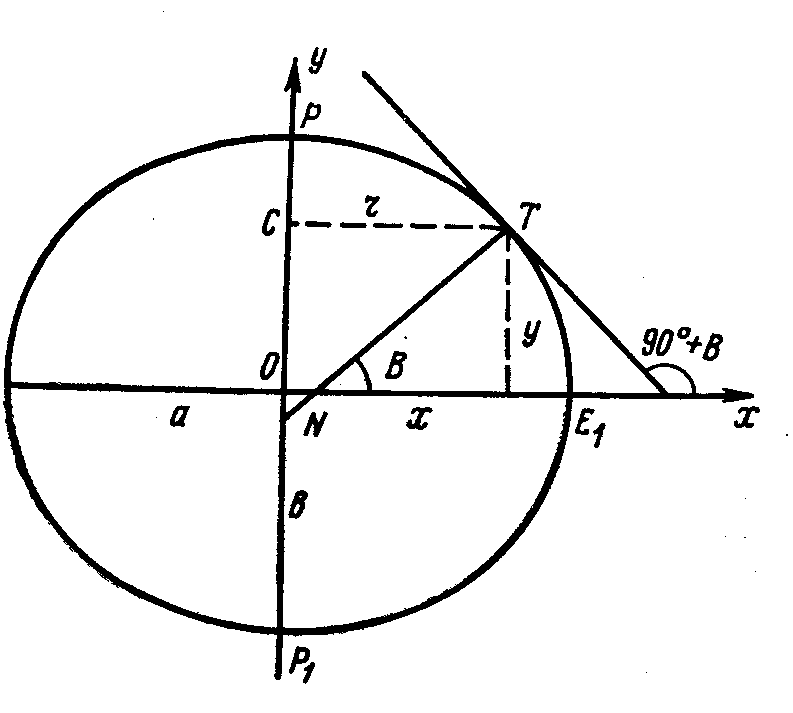
Рис. 10.2

Заменяя радиус параллели СТ (выражение , формула (9.9) из лекц. №2) его величиной получаем NT

; (10.5)

NT — нормаль в точке Т, поэтому можно сказать, что длина нормали равна радиусу кривизны первого вертикала в этой точке.

Радиус кривизны меридиана применяется при вычислении длин дуг меридиана и разности широт точек, радиус кривизны первого вертикала — при вычислении длин дуг параллелей, разности долгот и разности азимутов.

Средний радиус кривизны можно провести из данной точки, когда число их стремится к бесконечности. Меридианное сечение и сечение первого вертикала являются главными нормальными сечениями, имеющими соответственно максимальную и минимальную кривизну.

Таким образом, средним радиусом кривизны называется среднее арифметическое из радиусов кривизны всех возможных нормальных сечений, проводимых на эллипсоиде в данной точке. Величина R среднего радиуса кривизны определяется формулой

. (10.5^*)

Выражение (10.5^*) может быть написано в функции величин W и V так:

, (10.6)

где с – радиус кривизны меридианного эллипса в полюсах .

Средний радиус кривизны применяется, когда Землю принимают за шар, а также при вычислении сферических избытков треугольников.

В таблицах даются через интервалы по широте в 1΄ величины [1], [2], R, а также функции V.