6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

1. Складність алгоритмів, зведення задач, нижні оцінки складності задач

Час, який витрачається алгоритмом, як функція розміру задачі, називається часовою складністю цього алгоритму. Гранична поведінка цієї складності при збільшені розміру задачі називається асимптотичною часовою складністю.

Аналогічно, можна виділити об’ємну складність та асимптотичну об’ємну складність.

Оцінки складності:

• верхні оцінки: ;

• нижні оцінки: ;

• ефективні оцінки: ;

Позначенням визначаються функції, нехтувано малі у порівнянні з функцією . Вони визначаються умовою .

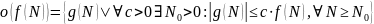Зведення задач. Метод зведення використовується для встановлення оцінки складності однієї задачі за відомою оцінкою складності іншої задачі.

Нехай маємо задачу 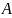та задачу 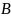. Кажуть, що задача та перетворюється (зводиться) до задачі , якщо:

1. Початкові дані задачі перетворюються на відповідні початкові дані задачі .

2. Розв’язується задача .

3. Розв’язок задачі (вихідні дані) перетворюється у правильний розв’язок задачі .

Якщо кроки 1 та 3 можна виконати за час 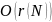, де – розмір задачі , то кажуть, що задача є -звідною до задачі . Цей факт позначають так: .

Зводимість не є симетричним відношенням. Якщо задачі та взаємно звідні, то вони називаються еквівалентними.

Нижні оцінки методом перетворення: Якщо відомо, що задача вимагає щонайменше 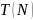часу, і , то задачу можна розв’язати за час не менший за .

Верхні оцінки методом перетворення: Якщо відомо, що задачу можна розв’язати за час , і , то задачу можна розв’язати за час, який не перевищує .

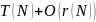Відомі нижні оцінки складності деяких задач:

• Для скінченної 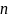-елементної множини перевірка умови вимагає часу ;

• Для впорядкування сукупності з елементів необхідно часу ;

• Якщо деяка задача у 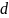-вимірному просторі вимагає 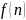часу, то для цієї ж задачі розмірністью 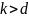також потрібно принаймні часу;

• Задачі із нижньою оцінкою складності :

  • перевірка того, чи є у заданій сукупності два рівних елементи;

  • перевірка включення множин;

  • перевірка перетину множин;

  • перевірка на значимість: дано точок на площині, визначити, чи усі вони належать опуклій оболонці;

  • перевірка -близькості: чи є серед елементів заданої -елементної множини два елементи, які знаходяться на відстані .

6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

2. Дерево відрізків та реберний список з подвійними зв’язками

6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

3. Локалізація точки на планарному розбитті. Методи

6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

4. Регіональний пошук. Методи

Задача. На заданій множині S із N точок задано запитний регіон R. Знайти підмножину точок множини S ( або їх кількість), які містяться в регіоні R.

Одновимірний регіональний пошук. Множина з N точок на осі x являє файл, а запитним регіоном є відрізок [x',x"] ( який називається x- регіоном). Ефективний регіональний пошук реалізується через метод, який базується на методі двійкового пошуку. Структура даних, яка забезпечує вказану дію, є прошите двійкове дерево, т.т. таке збалансоване двійкове дерево, листки якого додатково зв’язані у списку, який виражає порядок абсцис; дерево і список обробляються на фазах відповідного пошуку й вибірки. Оцінки: оптимальна як по часу запиту q(logN+k), так і по пам’яті q(N).

Алгоритм 2-D-дерева. (складність попередньої обробки: 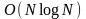, пошуку: 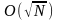). Означення. Назвемо узагальненим прямокутником таку область на площині, яка визначена декартовим добутком [x₁, x₂]´[y₁,y₂] x- інтервалу - [x₁, x₂] та у – інтервалу - [y₁,y₂], включаючи граничні випадки, коли в довільній комбінації допускається: x₁= - ¥, x₂ = ¥, y₁= - ¥, y₂ = ¥.

Нехай задана множина S із N точок на площині. Для побудови структури даних, яка називається “2-D дерево” використовується схема “розподіляй та володарюй” суть якої полягає в рекурсивному розбиті площини на прямокутники R(v), означені вище. Результатом розбиття є бінарне дерево пошуку, вузлами якого є точки із заданої множини S на площині.

П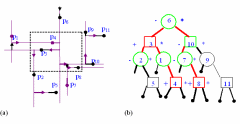 роектуються усі точки множини S на вісі ОХ та ОУ. Знаходиться медіана списку точок впорядкованих по х, проводиться вертикаль. Точка буде коренем шуканого дерева і розіб'є список на дві рівнопотужні підмножини, для яких існують списки вопрядковані по у. Для них визначаються медіани і будуються горизонталі. Ті точки будуть наступними вузлами шуканого дерева. Для зручності при побудові шуканого дерева ведемо позначення для вузлів трьох різних типів: кружки - не листові вузли з вертикальною лінією розрізу, квадрати - не листові вузли з горизонтальною лінією розрізу, точки - листки.

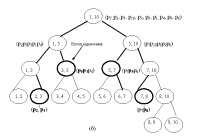
Метод дерева регіонів. (складність попередньої обробки: 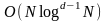, пошук: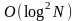 ) . Будується дворівнева структура даних (дерево регіонів), перший рівень якої – дерево відрізків по одній із координат (наприклад х), а другий – вузли дерева відрізків прошиті упорядкованими списками по іншій координаті (наприклад у ).На побудованому дереві регіонів виконується операції вставки інтервалу ( проекція запитного регіону на вісь ОХ ), що дозволяє визначити вузли віднесення. Далі у вузлах віднесення застосовується дихотомія пошуку по іншій координаті (у).

Метод прямого доступу: Площина розбивається на комірки прямими, що проходять через всі дані точки (пари комірок утворюються класи еквівалентності відносно результатів пошуку). Для кожнох пари комірок встановлюється відповідна множина точок. Для співставлення точки одній комірці - двійковий пошук по x, у координатам. Звертання до файлу - константа. Пам'ять O(N⁵)

6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

5. Побудова опуклої оболонки. Методи

6. Обчислювальна геометрія, комп’ютерна графіка та комп’ютерна алгебра

6. Найближча пара, метод «Розділяй та пануй»

Примітка1: часову оцінку складності сортування списку точок по координаті х віднесемо до попередньої обробки вхідної множини, в найгіршому випадку сортування буде потребувати O(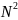 ), а в кращому O(Nlog2N). Сортування множини точок по координаті у можно виконувати за O( ) прямо під час кроку злиття двох вже відсортованих по у множин.

Примітка2: на етапі злиття, маючи відсортовані по y точки, ми розглядаємо відстань тільки між тими точками, між якими різниця ординат менше нашої мінімальної дистанції (а не відстань між всіма точками першої і другої множин).

Примітка3 (для тих, кто сумнівається, що крок 6 виконується за лінійний час):

Примітка4 (сама очевидність): щоб показати, що часова оцінка складності дійсно дорівнює O(Nlog2N) треба показати, що часова оцінка на кроці злиття дорівнює O( ), а враховуючи Примітку2 і Примітку3 бачимо, що це так і є.