31.Похідна оберненої функції.

Теорема.Нехай ф-я у=f(x) в деякому околі точки х₀ зростає(чи спадає) і є неперерв. Нехай, крім того, ф-я у=f(х) диференц в т.x₀ і похідна f ' (x₀)не=0. Тоді існує обернена ф-я х=f^-1(y), яка визначена в деякому околі відповід точки у₀=f(x₀), диференц в цій т. і має в цій т. похідну, що=1/f ' (x₀).

Довед. f(x)-неперерв і строго монот на О(х₀) строго монот непер f^-1(y), яка визначена на f(О(х₀)).

Якщо ∆х→0 ∆у→0. Якщо ∆хне=0 ∆уне=0.

Навпаки, якщо ∆у→0 ∆х→0.

Отже, .

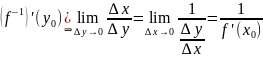Зауваження: Якщо f ' (х₀)=0, то (f^-1)'(y₀)=∞.

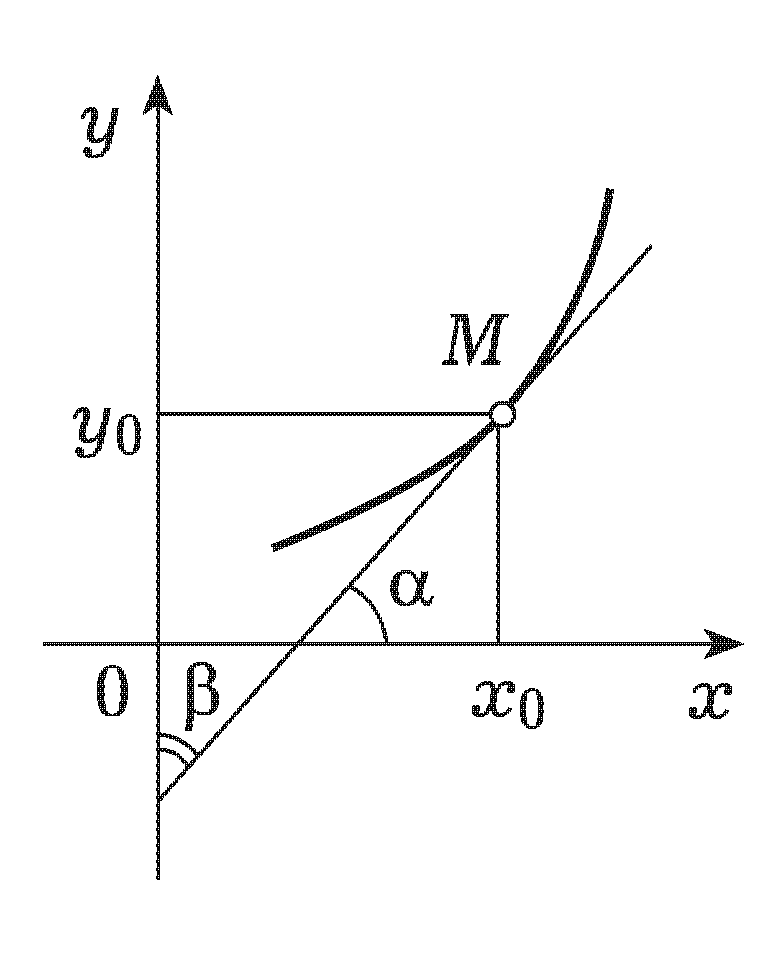Доведена теор має простий геомет зміст. Розглянемо в околі т. х₀ графік ф-ї у = f(x) (або оберненої ф-ї). Допустимо, що точці х₀ на цьому графіку відповідає т. М. Тоді, очевидно, похідна f'(x₀) =тангенсу кута нахилу дотичної, що проход через т. М, до осі Ох. Похідна оберненої ф-ї

{f^-1(y₀)}' = тангенсу кута нахилу β тієї ж дотичної до осі Оу. Так як кути α і β в сумі = π/2, то формула 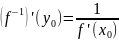виражає очевидний факт: tgβ=1/tgα.

32.Власт диференціалу.Інваріантність форми і-го диференціалу.

Виходячи з властивостей похідних та визначення диференціала, маємо правила диференціювання ф-й:

1)d(αy₁+βy₂)=αdy₁+βdy₂, α, βєR

2)d(y₁y₂)=y₂dy₁+y₁dy₂

3)d(y₁/y₂)=[y₂dy₁-y₁dy₂]/y₂², y₂(x₀)не=0.

Диференціали і ф-ї беруться в т.х₀.

Інваріантність форми І-го диференціалу: Якщо y=f(x)диференц в т.х₀, z=g(y) диференц в т.у₀, y₀=f(x₀), то складена ф-я z=F(x) диференц в т.х₀ та виконується: dF(x₀)=dz(x₀)=F'(x₀)dx=g'(y₀)dy.

Зауваження: Форма 1-го диференц не залеж(інваріантна) від того, чи змінна є незалеж(х) чи залеж(y=f(x)).

Довед.dF(x₀)=F'(x₀)dx=g'(y₀)f'(x₀)dx=g'(y₀)dy

dy

Ф-ла скінченних приростів:

.

33.Похідні основних елементарних функцій

Похідна степеневої ф-ї з будь-яким вещественным показником. Визначимо похідну стереневої ф-ї у=х^α з будь-яким вещественным показником α. Ми будемо знаходити похідну цієї ф-ї для тих знач х, для яких ця ф-я визначена при будь-якому α, а саме для знач х, що належ півпрямій х > 0. Маючи на увазі, що всюди на півпрямій х > 0 ф-я у=х^α додатня, знайдемо логарифм похідну цієї ф-ї. Так як Inу = αInх, то логарифм похідна має вигляд: .

Звідси, враховуючи, що у=х^α, отримаємо ф-лу похідної степеневої ф-ї:

.

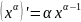Елементарна ф-я - така ф-я, що виражається через найпростіші елементарні ф-ї шляхом 4-х арифм дій та суперпозицій, послідовно застосованих скінченне число разів. Можна стверджувати, що похідна б-я елементарної ф-ї є також елементарною ф-єю. Таким чином операція диференціювання не виводить нас з класу елементарних ф-й.

Таким чином, можна знайти похідні осн елементар ф-й:

1°. . Як часткові випадки: (1/x)'=-1/x²; .

2°. Як частковий вип. (lnx)'=1/x

3°. (а^x)' = а^x lna ). Як частковий вип., (e^x)' = е^x.

4°. (sinx)' = cos x.

5°. (cosx)' = -sinx.

6°. (tgx)' = 1/cos²x= 1 + tg²x; (xне=π/2+πn, де n = 0, ±1,...).

7°. (ctgx)'=-1/sin²x=-(1+ctg²x)(xне=πn, где n = 0,±1, ...).

8°. (arcsin x)'=1/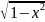 (-1<x<1).

9°. (arccos x )' = - 1/ (-1 < x < 1).

10°. (arctg x)'=1/1+x²

11°.(arcctg x)'=-1/1+x²

Якщо ввести гіперболічні ф-ї у = shx, у = chx, у = thx та у = cthx, які є простими комбінаціями степеневих ф-й, то з визначення цих ф-й елементарно випливають наступні вираження для їх похідних:

12°. (shx)' =chx

13°. (chx)' =shx

14°. (thx)'=1/ch²x

15°. (cthx)'=-1/sh²x(xне=0).