
- •1. Основні властивості нескінченно малих послідовностей.
- •2. Теорема Больцано-Вейєрштрасса
- •3. Поняття фундамент послідов.Фундаментальність збіж послідов.
- •4. Єдиність границі послідовності.
- •5. Перехід до границі послідовності у нерівностях.
- •6. Монот послідовності. Ознака збіжності монотонної послідовності.
- •7.Теореми про границю суми, добутку, віднош чп.
- •8. Критерій Коші збіжності числової послідовності.
- •9. Число як границя збіжної монотонної послідовності.
- •11. Озн. За Гейне границі ф-ї. Точка дотикання множини
- •12. Властивості границь функцій.
- •13. Нескінченно малі функції.
- •14. Порівняння функцій в околі заданої точки. Символи Ландау.
- •15. Критерій Коші існування границі функції.
- •16. Границі монотонних функцій.
- •17. Перша чудова границя.
- •24. Друга чудова границя.
- •19. Еквівалентні функції.
- •20. Поняття неперервності функції в точці. Одностороння непер-сть.
- •21.Різні форми запису неперервності функції в точці.
- •22. Неперервність оберненої функції.
- •23. Теорема Вейєрштраса про неперервну на відрізку функцію
- •24. Теорема Больцано-Коші.
- •25.Поняття похідної. Геометричний, механічний та ек зміст похідної
- •26.Зв'язок неперервності та диференційованості.
- •27.Необхідна та достатня умова диференційованості ф-ї.
- •28.Поняття диференціалу.Геометрич та механіч зміст диференціалу.
- •31.Похідна оберненої функції.
- •32.Власт диференціалу.Інваріантність форми і-го диференціалу.
- •33.Похідні основних елементарних функцій
- •34.Похідні вищих порядків, їх властивості.
- •35.Диференціали вищих порядків, їх властивості.
- •36.Теорема Ферма.
- •37.Теорема Ролля. Її геометричний зміст.
- •38.Теорема Лагранжа про скінченний приріст, її геометричний зміст.
- •39.Теорема Коші про середнє значення.
- •40. Перше правило Лопіталя.
- •41.Формула Тейлора та Маклорена з залишковим членом у формі Пеано.
- •42.Формула Тейлора з залишковим членом у формі Лагранжа.
- •43.Необхідна та достатня умова монотонності функції на інтервалі.
- •44. Екстремум функції. Необхідна умова внутрішнього локального екстремуму
- •45. Достатні умови екстремуму (використ першої похідної).
- •46.Достатні умови екстремуму (використання похідних вищих порядків). __
- •47.Опуклість функції. Геометричне визначення за допомогою хорд.
- •48.Необхідні та достатні умови опуклості функції.
- •49.Поняття точки перегину. Необхідні умови точки перегину.
- •50.Достатні умови точки перегину.
- •51.Поняття асимптоти. Визначення параметрів похилої асимптоти.
- •52.Лема про функції, що мають однакові похідні на інтервалі. Поняття первісної функції. Поняття невизначеного інтегралу, його властивості. Таблиця інтегралів.
- •53.Заміна змінної у невизначеному інтегралі та інтегрування частинами.
- •54.Інтегрування раціональних дробів.
- •55.Інтегрування тригонометричних виразів, універсальна тригонометрична підстановка.
- •56.Інтегрування найпростіших ірраціональних функцій.
- •57.Поняття інтегральної суми. Поняття визначеного інтеграла Рімана. Необхідна умова інтегрованості функції за Ріманом.
- •58.Поняття верхньої та нижньої сум Дарбу. Вла-сті сум Дарбу. Формулювання критерію інтегрованості.Приклади застосування.
- •59. Поняття рівномірно неперервної функції. Формолювання теореми Кантора про рівномірну неперервність непер ф-ції. Інтегрованість непер ф-ції.
- •60. Інтегрованість ф-ції, монотонної на відрізку. Інтегрованість обмеженої ф-ції, що має скінчену к-сть точок розриву.
- •61. Властивості визн інтегралу, що пов’язані з підінтегральною ф-цією, з відрізком інтегрування і визн нерівностями.
- •62. Теореми про середнє значення інтеграла Рімана.
- •63. Неперервна залежність визначеного інтегралу від змінної верхньої границі. Похідна інтегралу по змінній границі. Формула Ньютона-Лейбніца.
- •64. Заміна змінної у визначеному інтегралі, її геометричний зміст.
- •65. Формула інтегрування частинами для визначеного інтегралу.
- •66. Поняття площі плоскої фігури.
- •67. Критерій квадровності плоскої фігури. Приклад необмеженої фігури скінченної площі.
- •68. Обчислення площ і довжин дуг кривих. Обчислення об’ємів просторових фігур.
- •69. Невласні інтеграли першого і другого роду. Критерій Коші збіжності невласного інтегралу.
- •70. Невласні інтеграли від невід’ємних ф-цій.
- •71.Абсолютно і умовно збіжні невласні інтеграли. Приклади.
- •72. Ознаки збіжності та розбіжності невласних інтегралів. Еталонні інтеграли.
- •73. Ознаки Діріхле та Абеля збіжності невл інтеграла.
67. Критерій квадровності плоскої фігури. Приклад необмеженої фігури скінченної площі.
Якщо μ(X) скінчене є R, то Х наз квадровною або вимірною.
μ(X)- міра Х.
Озн-ня : μ*(X)= sup μ(E), E ∁ X/
μ*(X)= inf μ(E), E ) X
E, E - многокутники.
μ(Х)= μ*(X)= μ*(X) – тоді Х вимірна.
Якщо Х обмежена, то її площа скінчена.
Якщо Х необмежена, то взагалі кажучи, μ(Х)= + , але існують необмежені фігури скінченної площі.
Приклад. Необмежена фігура, але площа скінченна.
Площа стартового квадрату = 1.

 +
+
 +
+
 + ….=
+ ….=
 = 1
= 1
(площа вежі)
68. Обчислення площ і довжин дуг кривих. Обчислення об’ємів просторових фігур.
Т.: Якщо ф-ції х=φ(t) I y=Ψ(t) мають на сегменті [α,β] неперервні похідні, то крива L, визначена параметричними рівняннями, напрямлена і довжина l її дуги може бути вирахувана по формулі:

Якщо ф-ції х=φ(t) і y=Ψ(t) і х(t) мають на сегменті [α,β] неперервні похідні, то крива L, може бути вирахувана по формулі:
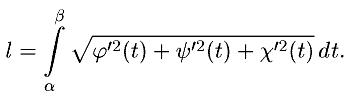
Якщо крива L є графіком ф-ції у=f(x), що має на сегменті [a,b] непевну похідну f/(x), то крива L мпрямляєма і довжина l дуги L ….:
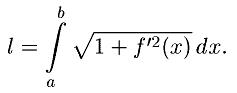
Нехай ф-ція у=f(x) неперервна на сегменті [a,b]. Тоді тіло Е, утворене обертанням навколо осі Ох криволінійної трапеції, обмеженої гр.-ком ф-ції f(x),ординатами в точках a і b і відрізком осі Ох від a до b, кубуюче і його об’єм V може бути знайдений по формулі:
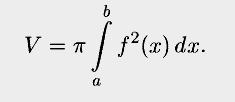
69. Невласні інтеграли першого і другого роду. Критерій Коші збіжності невласного інтегралу.
Нехай
ф-ція f(x) визначена на х є [a,b]; Припустимо,
що
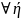 є [a,b] ф-ція f(x) інтегрована на [a,
є [a,b] ф-ція f(x) інтегрована на [a, ]
Тоді існує F(
)
=
]
Тоді існує F(
)
=
 dx
і ця ф-ція є непер на [a,b)
dx
і ця ф-ція є непер на [a,b)
НВІ
ф-ції
f(x) [a,b) наз границя
 dx
=
dx.
dx
=
dx.
Якщо границя існує і скінчена, то НВІ наз збіжним(існує);
Якщо границя не існує або нескінчена, то НВІ не існує;
Якщо границя нескінчена, то НВІ наз розбіжним.
Визначений інтеграл є частинним випадком невласного інтегралу:
Якщо b є R, f(x) – інтегрована на [a,b] dx.-----ВІ.
F(
)→
F(
),
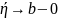
Розрізняють НВІ:
І роду: b=+ , f(x) інтегрована на [a, ], є [a; + )
 dx
=
dx
=
 dx
dx
ІІ роду: b є R, f(x) не обмежена в б.-я. околі т В.
dx = dx
Ознака Коші:
Т:
dx
– збіжний ↔
ε >0
ή є [a,b) таке, що
/,
//
є [ή,b) виконується | dx|<ε.
dx|<ε.
Доведення: Теорема є переформулюванням ознаки Коші існування границі ф-ції F( ) = dx
70. Невласні інтеграли від невід’ємних ф-цій.
Т:Якщо
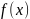 ≥
0,х є [a,b),то
dx
збіжний ↔
с>0 таке,що
ή є[a,b) викон
dx
≤ с (множина інтегралів обмежена)
≥
0,х є [a,b),то
dx
збіжний ↔
с>0 таке,що
ή є[a,b) викон
dx
≤ с (множина інтегралів обмежена)
Дов.:
інтеграл збіжний, якщо існує скінченна
 є R;
є R;
 =
= dx.
Так як
≥
0 беремо
/>ή,
тоді
dx.
Так як
≥
0 беремо
/>ή,
тоді
 =
= dx
=
dx
+
dx
=
dx
+
 dx
≥
dx
≥

Отже,
 ,
,
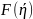 ≤с→
існує
є R.
≤с→
існує
є R.
Т.(Ознака порівняння): Якщо 0≤g(x)≤f(x), x [a,b), тоді:
1)
dx
збіжний →
 dx
збіжний
dx
збіжний
2) dx розбіжний → dx розбіжний
Дов:1)
попередня теорема→
dx
обмежена,
ή є[a,b)→за властив НВІ →
 dx
≤
dx
→
dx
обмежена →
dx
збіжний.
dx
≤
dx
→
dx
обмежена →
dx
збіжний.
2) Від супротивного. Нехай dx розбіжний, а dx збіжний →
dx обмежена, ή є[a,b) → dx ≤ dx → dx обмежена → dx збіжний, що суперечить умові.
Наслідок. (Гранична ознака порівняння).
Нехай
ф-ція
≥
0,
> 0, х є [a,b) та нехай існує
 =
k, тоді 1) якщо
dx
збіжний та 0 ≤ k <
=
k, тоді 1) якщо
dx
збіжний та 0 ≤ k <
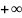 ,
то
dx
збіжний.
,
то
dx
збіжний.
2) якщо dx розбіжний та 0 ≤ k < , то dx розбіжний.
