7.3.Построение градуировочного графика методом наименьших квадратов, мнк.
Если установлено, что разброс точек является следствием случайных погрешностей, то метод МНК позволяет найти положение графика, наилучшим образом отражающее искомую зависимость. Градуировочный график строят по экспериментально полученным точкам, в координатах: концентрация (по оси Х)– аналитический сигнал (по оси У).
Если доказана линейная зависимость аналитического сигнала от концентрации (уравнение 7.5) то задача МНК сводится к тому, чтобы найти такие значения коэффициентов «a» и «b», при которых сумма квадратов расстояний точек снизу от прямой, равна сумме квадратов расстояний точек
сверху от прямой. Иначе говоря, сумма квадратов отклонений экспериментально полученных точек от прямой минимальна.
Y = aХ + b……..7,5
Коэффициенты линейного уравнения «a» и «b» можно рассчитать по следующим формулам:
7,6
а – тангенс угла наклона графика относительно оси Х. (рис.7.1)
b - отрезок, отсекаемый графиком на оси Y.
Xi - концентрация аналита в градуировочном образце.
Y – аналитический сигнал.
Как видно из формул, расчет этих коэффициентов достаточно трудоемкий процесс. Значение коэффициентов можно легко найти с помощью компьютера. Надо в программе «Excel» выбрать категорию «Статистические»,
- значение коэффициента «а» найти как функцию «НАКЛОН»,
- значение коэффициента «в» - «ОТРЕЗОК».
Определив значения «a» и «b», для стандартных (градуировочных) образцов, подставляют их значения в уравнение 7.5 и рассчитывают ординаты (Y) точек. По полученным точкам строят градуировочный график. (Рис. 7.1)
Градуировочный график можно построить и другим способом - с помощью компьютера. (С этим способом мы познакомимся позже на практических занятиях)
На рисунке 7.1. показаны градуировочный график, уравнение, отражающее линейную зависимость аналитического сигнала от концентрации аналита с указанием коэффициентов (а=53,75; в=0,595) и значение R2,.
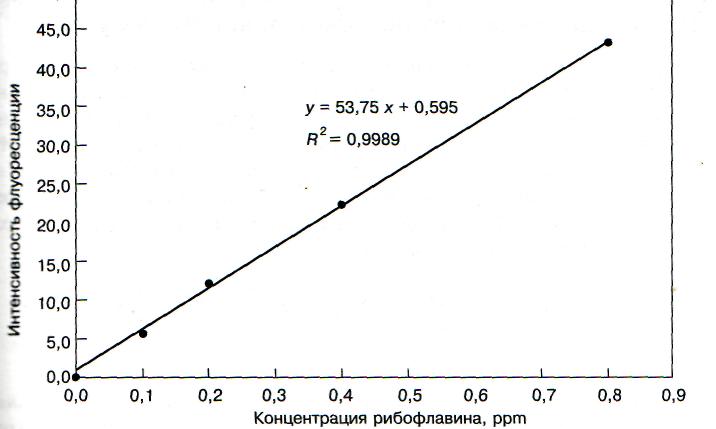
Рис.7.1. Градуировочный график для определения концентрации железа в яблочном соке, построенный методом наименьших квадратов
В некоторых приборах (например – СФ-46, КФК - 3) можно внести значения коэффициентов «а» и «в» в память встроенного микропроцессора. После этого на шкале прибора сразу можно получить значение концентрации аналита.
В современных приборах состыкованных с компьютером, имеются программные обеспечения (П.О), позволяющие после введения концентраций всех градуировочных образцов и измерения аналитических сигналов получить на мониторе готовый градуировочный график и уравнение его описывающее. К таким приборам относятся :
1. Атомно-эмиссионный спектрометр «ПАПУАС 4ДИ»
2. Атомно-абсорбционные спектрометры типа «КВАНТ»
3. Рентгено-флуоресцентные спектрометры серии «Спектроскан» и множество приборов для молекулярного спектрального анализа.
Перечисленные приборы имеются в лаборатории спектрального анализа ПК №39.
7.3. Определение концентрации аналита в анализируемом образце с помощью градуировочного графика и градуировочного уравнения.
Концентрацию аналита в анализируемом образце можно определить по градуировочному графику. Для этого надо несколько раз (3-5) провести анализ исследуемого образца. Измерить аналитический сигнал аналита в условиях повторяемости. Рассчитать среднее значение аналитического сигнала и по градуировочному графику определить концентрацию.
Можно определить концентрацию аналита без построения градуировочного графика, использую градуировочное уравнение.
Зная коэффициенты градуировочного уравнения, нетрудно рассчитать концентрацию аналита в исследуемом образце по формуле.
(7.7)
Пример. Для определения концентрации (ppm) железа в яблочном соке, определили коэффициенты градуировочного уравнения по стандартным образцам (Рис. 7.1). Y=53,75Х + 0,595; а=53,75; b=0,595
Выполнили три измерения аналитического сигнала для исследуемого образца и получили значения: Y1=22,51; Y2= 22,44; Y3 =22,66.
Каждое из трех значений Y подставили в уравнение 7.7 и рассчитали три значения концентрации:
Х1=(22,51- 0,595)/ 53,75=0,408; Х2=(22,44 - 0,595)/ 53,75=0,406
Х3=(22,66- 0,595)/ 53,75=0,411
