22. Інтегрування раціональних функцій.

Розглядаємо невизначені інтеграли від неперервних функцій. Нас цікавить, коли вони виражаються через скінчену кількість елементарних функцій. Випадок, коли інтеграл виражається через скінчену кількість елементарних функцій називається взяття інтеграла в скінченому вигляді в квадратурах або інтегрування в скінченому вигляді. Є багато невизначених інтегралів, які не беруться в скінчених квадратурах.

Нам потрібно виділити класи підінтегральних функцій, щоб інтеграл від них брався в скінчених квадратурах. 1.Раціональні або дробово-раціональні функції:

Найпростішим представником цього класу є многочлен:

Дробово-раціональна функція – відношення двох многочленів та

2.Прості дроби

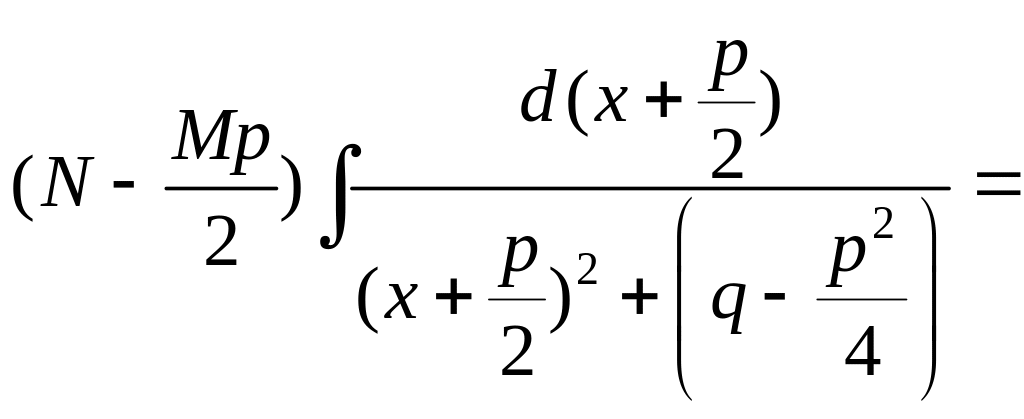
3.Інтегрування правильних дробів

Маємо правильний дріб .Розглянемо знаменник дробу . Розкладемо його на добуток незвідних многочленів над R.

,де

дійсний корінь кратності дійсний корінь кратності . -многочлени, які не мають дійсних коренів.

Правильний нескоротний дріб має вигляд:

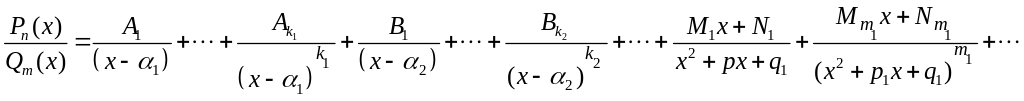
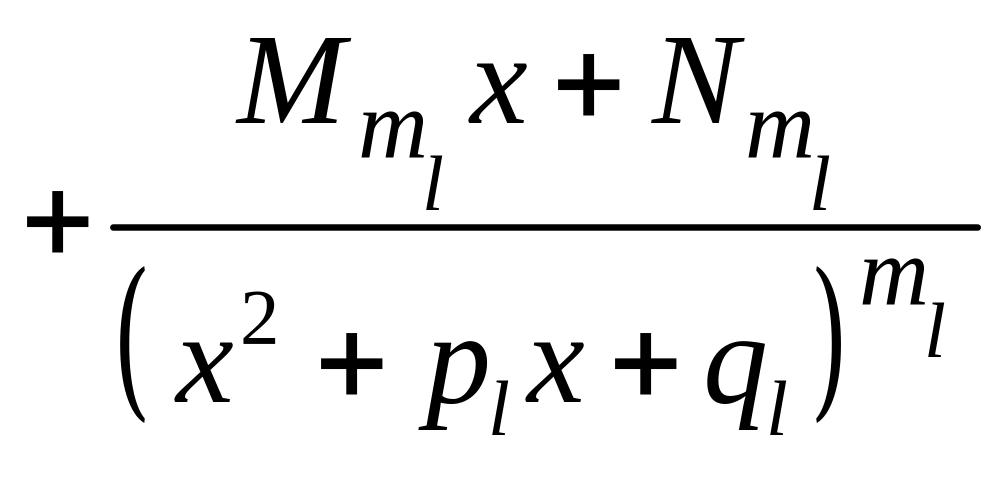Кожний доданок вміємо інтегрувати.

Метод невизначених коефіцієнтів:

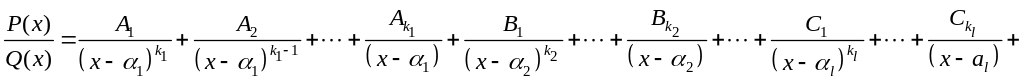
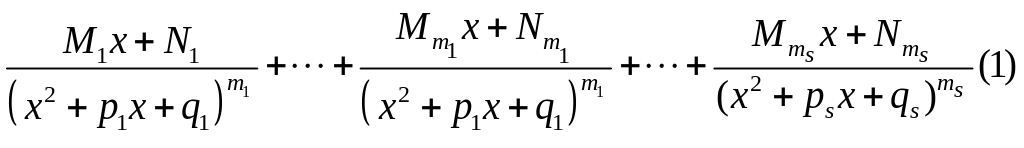
Коефіцієнти (2) визначаються однозначно.

Правильний нескоротний дріб представимо у вигляді (1) з коефіцієнтами (2). Зводимо до спільного знаменника і прирівнюємо P(x) до чисельника зведеного дробу. Коефіцієнти при однакових степенях х повинні бути рівні. Прирівнюємо коефіцієнти і знаходимо їх з отриманих рівнянь. Потім можемо інтегрувати уже суму простих дробів.

Виділення раціональної частини при інтегруванні раціональних функцій.(Метод Остроградського). Обчислимо , ,

Покажемо, що .(3) і - многочлени з невизначеними коефіцієнтами, які шукаються методом невизначених коефіцієнтів однозначно. розкладаються на дроби. 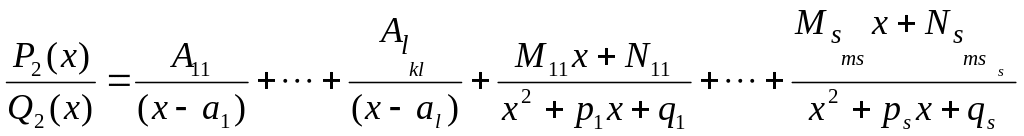.Нехай виконується рівність(3).Візьмемо зліва і справа похідну.

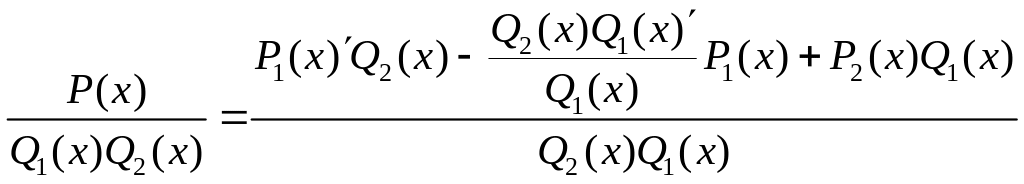
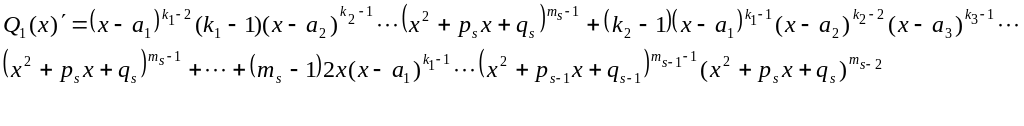
Якщо домножимо похідну на , то в кожному доданку множником буде , тому - многочлен, а отже - многочлен. Тому в чисельнику ми маємо многочлен .З цієї рівності визначаються коефіцієнти цього многочленна.

Якщо замість аргумента деяка раціональна функція:

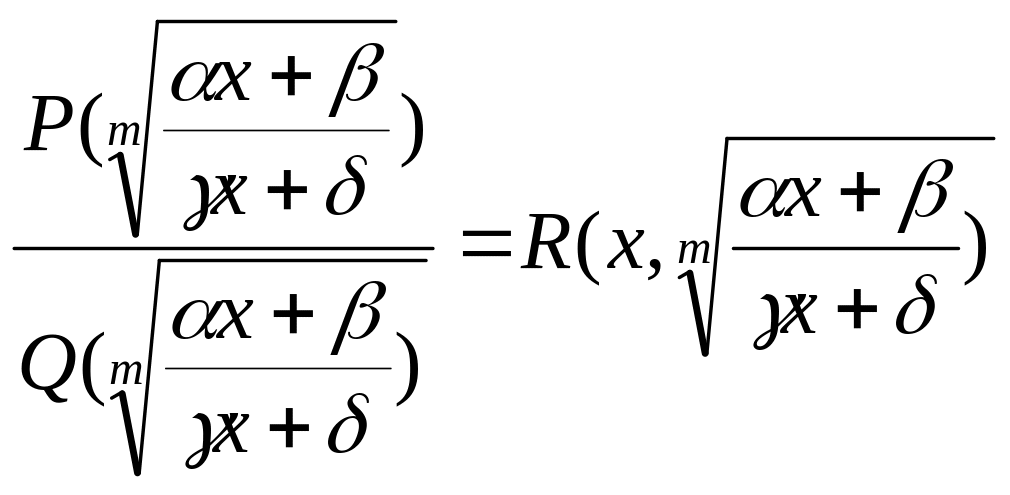
.Для того, Щоб знайти робимо заміну

Інтегрування раціональних функцій від тригонометричних аргументів.

Розглянемо раціональну функцію R(u,v). Нехай u=sin(x), v=cos(x), то R(sin(x), cos(x)) -неперервна по x. Знайдемо .Зробимо універсальну підстановку x=2arctg t

= =

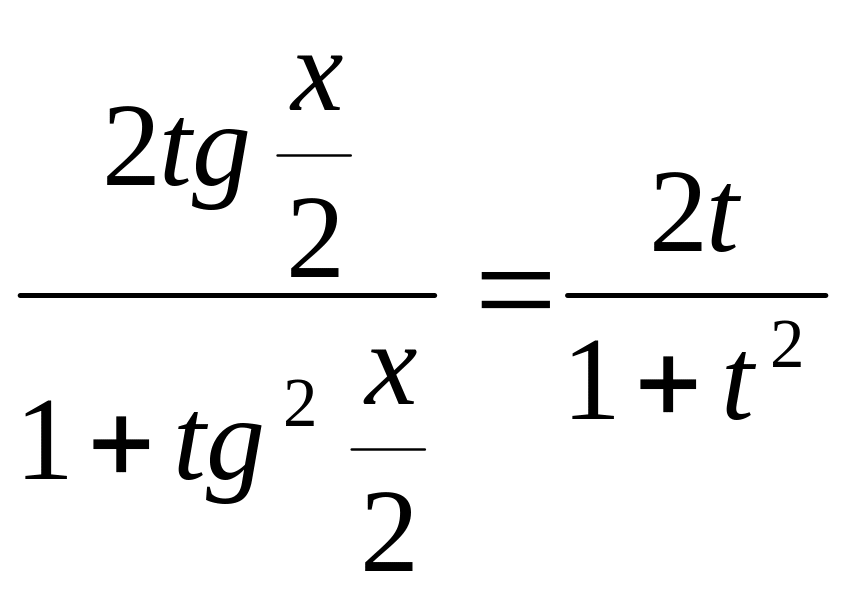
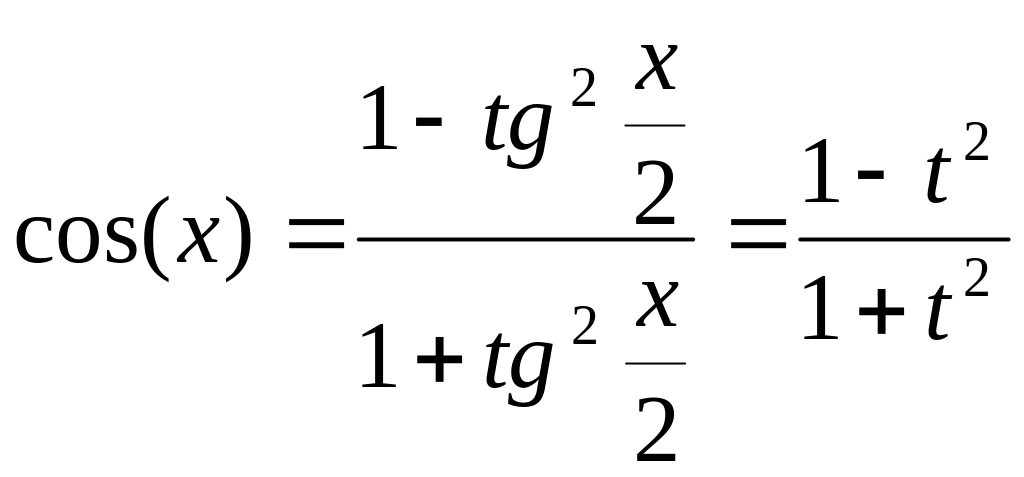
23.Означений інтеграл. Необхідна умова інтегровності. Необхідні і достатні умови інтегровності.

Нехай визначена на відрізку . Відрізок розбиваємо на частини , . На кожній частинці виберемо довільну точку .Обчислимо значення функції в цій точці і помножимо на .

Утворимо суму

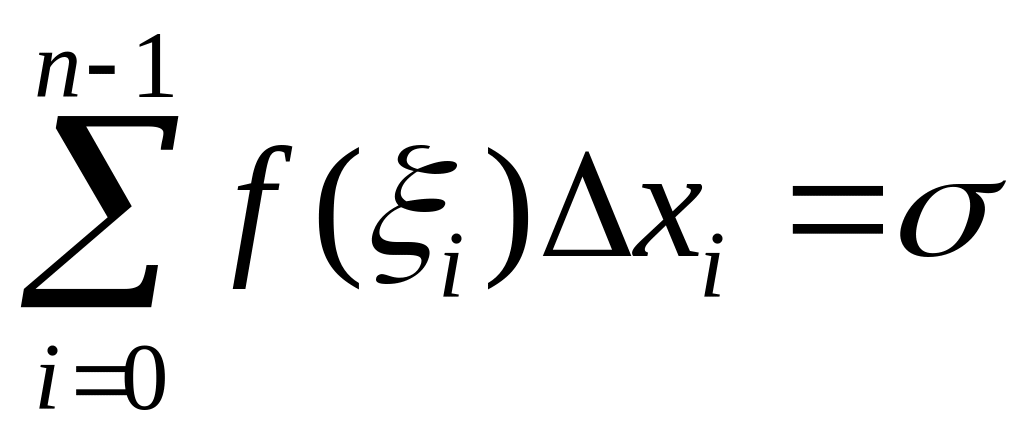- інтегральна сума Рімана для на відрізку .

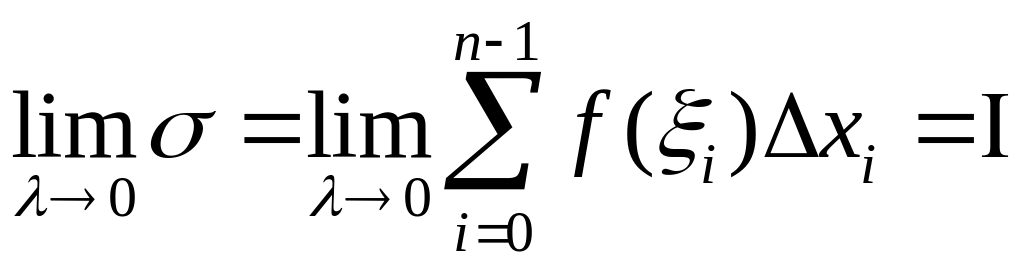. Якщо границя існує скінчена, не залежить від вибору точок і поділу відрізка на частини, то цю границю називають визначеним інтегралом від функції

на відрізку . , нижня межа інтеграла, верхня межа інтеграла.

Дамо означення цієї границі на мові (за Коші):

Якщо таке, що як тільки то незалежно від вибору точок і способу поділу відрізка на частини.

Означення границі на мові послідовностей(за Гейне).

Візьмемо поділ відрізка і знайдемо при цьому поділі , другий поділ, , що відповідає другому поділу. Позначимо ий поділ, , що відповідає му поділу. Послідовність поділів називають основною послідовністю поділів, якщо відповідна послідовність .

Визначений інтеграл на мові послідовностей:

Якщо, яку б не взяли основну послідовність , то відповідна їм послідовність незалежно від вибору точок , то говорять, що

Якщо , то функція інтегровна за Ріманом на . Позначають .

Необхідна умова інтегровності.

Нехай функція інтегровна за Ріманом на , то обмежена на відрізку ,тобто необхідною умовою інтегровності є обмеженість.

Покажемо це.

Нехай функція - інтегровна за Ріманові необмежена зверху. Тоді, якщо будемо відрізок розбивати на частини, то завжди знайдеться частина , на якій необмежена. Вибираючи точки так, щоб було як завгодно великим, тоді інтегральна сума також стане необмеженою, як завгодно великою, що суперечить тому, що має скінчену границю при , яка не залежить від вибору точок .Одержали суперечність. Отже всяка інтегровна функція є обмеженою, але якщо функція обмежена то звідси не слідує, що вона інтегровна за Ріманом.

Введемо суми Дарбу.Шукаємо

- нижня сума Дарбу - верхня сума Дарбу