19. Асимптоти графіка функції. Знаходження асимптот.

Розглянемо . Якщо , , , де -скінченне число, то пряму називають вертикальною асимптотою графіка функції . Якщо , де -скінченне число, то ­ називають горизонтальною асимптотою графіка функції .

Пряма є похилою асимптотою графіка функцій .

Теор. Для того, щоб існувала - похила асимптота необхідно і досить, щоб існували (1) і (2).

Дов. Оскільки різниця ординат тільки сталим множником (рівним косинусу кута між асимптотою і віссю ) відрізняється від відстані , то при одночасно з повинна прямувати до нуля і ця різниця: . (3). Розділивши на , одержимо , крім того з (3) отримаємо . Тепер навпаки, нехай маємо (1) і (2). З (2) отримаємо (3): , то і прямує до нуля, а косинус кута між асимптотою і віссю – величина обмежена. Звідси випливає .Аналогічно доводиться, коли . Теор. доведена.

20. Первісна функція, властивості. Таблиця первісних.

Розглянемо таку задачу: прискорення задано як функція від часу : . Потрібно знайти швидкість і шлях в залежності від . Тобто, тут потрібно за функцією відновити ту функцію , для якої буде похідною, а потім, знаючи функцію , знайти ту функцію , для якої похідною буде .

Функція на даному проміжку наз. Первісною для функції або інтегралом від , якщо на всьому цьому проміжку буде похідною для функції або, що служить для диференціалом: або .

ТЕОРЕМА. Якщо в деякому проміжку функція є первісною для функції , то і функція , де -будь-яка стала, також буде первісною. І навпаки: кожна функція, первісна для на проміжку , може бути представлена в такому вигляді.

Доведення: Те, що разом з і буде первісною для є очевидним, бо .Нехай - довільна первісна для функція, так що на проміжку . Так як функції і на даному проміжку мають одну і ту ж похідну, то вони відрізняються на похідну: . Доведено.

Отже, , де - довільна стала, являє собою загальний вигляд функції, яка має похідну або диференціал . Дане означення – це означення невизначеного інтеграла і позначається , де - підінтегральний вираз, а - підінтегральна функція. Звідси випливають такі властивості:

1. . 2. або .

Повертаючись до задачі, сформульованої на початку, тепер ми можемо записати і . Властивості:

1. Якщо - стала , то .

Дов. .

2. .

Дов. .

3. .

Дов. ,тоді .Таб.Первісних:

. . . . . . . . . . . . . .

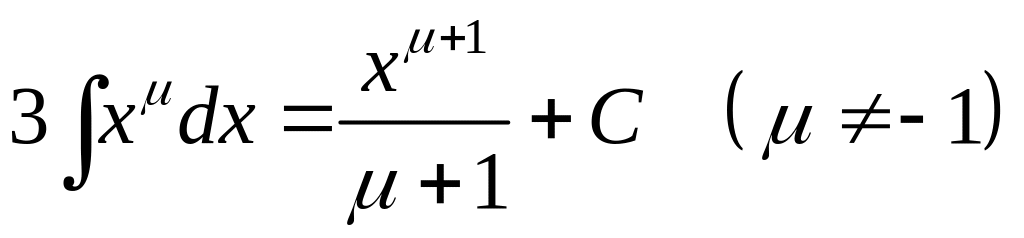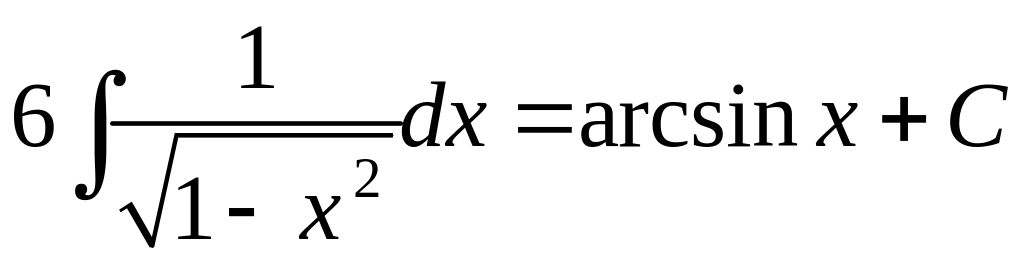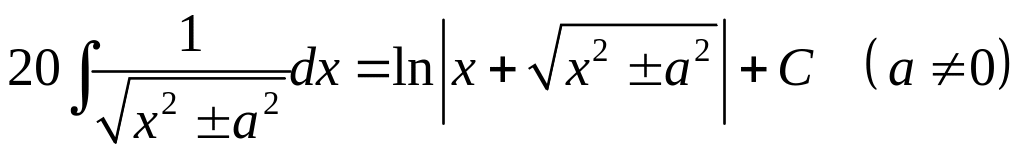21. Заміна змінної та інтегрування частинами.

Інтегрування шляхом заміни змінної. В основі цього методу лежить таке зауваження: якщо відомо, що , то тоді .

Дійсно, , якщо врахувати, що , або .

Нехай потрібно обчислити такий інтеграл: . В багатьох випадках замість нової змінної вдасться вибрати таку функцію , щоб підінтегральний вираз набув такого вигляду: , де - зручніша для користування функція ніж . Тоді достатньо знайти такий інтеграл: , щоб після підстановки отримати шуканий інтеграл. Звичайно записують так: , враховуючи, що в функції від проведена вище вказана заміна.

Інколи роблять іншу заміну. А саме: в підінтегральнім виразі підставляють замість функцію від нової змінної і отримують в результаті такий вираз: .

Інтегрування частинами. Нехай і є дві функції від х, які мають неперервні похідні і . Тоді за правилом диференціювання добутку або . Для виразу первісною буде , тому має місце така формула: (1)- формула для інтегрування частинами. Вона приводить інтегрування виразу до інтегрування такого виразу: .

Правило інтегрування частинами має більш обмежену область використання ніж заміна змінних. Але є цілі класи інтегралів, наприклад, , , , і т. д., які обчислюються саме за допомогою інтегрування частинами.

Повторне використання правила інтегрування частинами приводить до загальної формули інтегрування частинами.

Припустимо, що функції і на деякому проміжку мають неперервні похідні до -го порядку включно: .

Замінивши в формулі (1) на , ми отримаємо

. Аналогічно, ,

,

.

Домножуючи дані рівності по черзі на +1 або на -1 і складаючи їх почленно по знищенню однакових інтегралів у правій і лівій частинах, ми прийдемо до такої формули: .

Особливо вигідно користуватися даною формулою, коли одним із множників підінтегральної функції є многочлен. Якщо являє собою многочлен -го степеня, то . І для інтеграла в лівій частині отримаємо кінцевий результат.