13. Диференціал. Інваріантність форми диференціала.

Означення диференціала. Нехай маємо функцію y=f(x), визначену на деякому проміжку Х і визначену в розглядуваній точці х₀. Тоді приросту Dх аргументу відповідає приріст

Dy=Df(x₀)=f(x₀+Dx)– f(x₀),

нескінченно малий разом з Dх. Більш важливим є питання, чи існує для Dy така лінійна відносно Dх нескінченно мала А·Dх (a=const), що їх різниця є, в порівнянні з Dх, нескінченно малою вищого порядку:

Dy=А·Dх+о(Dх). (1)

При А 0 наявність рівності (1) показує, що нескінченно мала А· Dх еквівалентна нескінченно малій Dy і, значить, служить для останньої її головною частиною, якщо за основну нескінченно малу беруть Dх.

Якщо рівність (1) виконується, то функція y=f(x) називається диференційованою (при даному значенні х=х₀), сам же вираз А·Dх називається диференціалом функції і позначається символом dy або df(x₀).

Диференціал функції характеризується двома властивостями:

а) він представляє лінійну однорідну функцію від приросту аргументу;

б) відрізняється від приросту функції на величину, котра при Dх®0 є нескінченно малою, порядку вищого ніж Dх.

Інваріантність форми диференціала. Правило диференціювання складної функції приведе нас до такої важливої властивості диференціала.

Нехай функції y=f(x) і x=j(t) такі, що містяться в складній функції y=f(j(t)). Якщо існують похідні і , то існує і похідна:

. (2)

Диференціал dy, якщо x – незалежна змінна, буде визначатись за формулою (3). Перейдемо тепер до незалежної змінної t; в цьому припущенні маємо інший вираз для диференціалу:

.

Роблячи заміну похідної її виразом (2) і враховуючи, що це диференціал x як функції від t, отримаємо

,

Тобто повертаємось до попередньої форми диференціалу!

Таким чином, форма диференціалу може бути збережена навіть в тому випадку, якщо попередня незалежна змінна замінена новою. Ми завжди маємо право записувати диференціал у формі (3), чи буде x незалежною змінною чи ні; різниця тільки в тому, що якщо за незалежну змінну вибрано t, то dx означає не довільний приріст Dх, а диференціал x як функції від t. Ця властивість називається інваріантністю форми диференціалу.

Оскільки з формули (3) безпосередньо можна отримати формулу, що виражає похідну через диференціали dx і dy, то і остання формула залишається в силі, за якою б незалежною змінною (однією і тією ж в кожному випадку) не були обчислені вказані диференціали.

Нехай, наприклад, , так що

.

Замінимо тепер . Тоді і ми отримаємо: .

14. Похідні і диференціали вищих порядків.

Якщо ф-я у= ,має похідну на деякому проміжку і якщо в кожній точці, то вона теж є функція. ( = –похідну від першої похідної наз. другою похідною. Якщо визначена в обл. , то її можна розглядати як нову ф-ю і шукати її похідну. Якщо похідна від другої похідної, то її наз. третьою похідною, позначають і т.д. Похідною -го порядку наз. пох. від ( -1) порядку. Нехай , .Розгл. її як ф-ю. Якщо ( то її наз. -ю похідною. Позначають , , .

По аналогії можна ввести поняття диф. вищих порядків. Нехай -диф. першого порядку визначений в , то він є ф-ю від . Якщо = то його наз. диф. другого порядку і т.д. = –наз. диф. -го порядку.

Загальні формули.

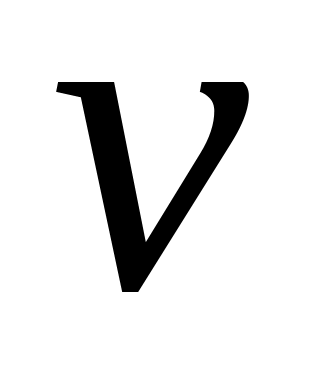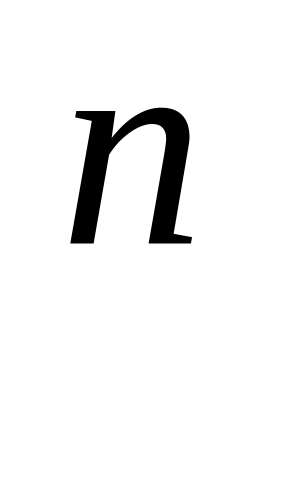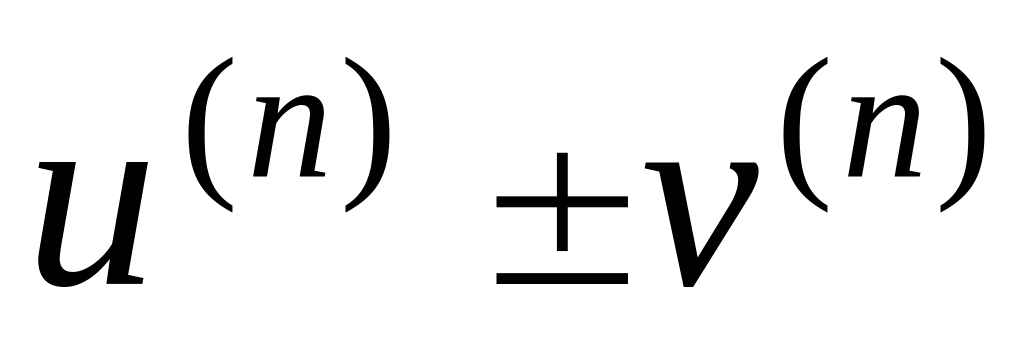1. ( ± ) = 2.

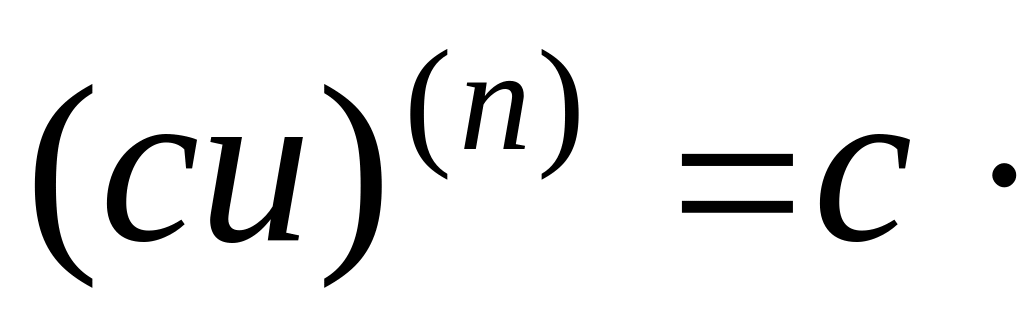
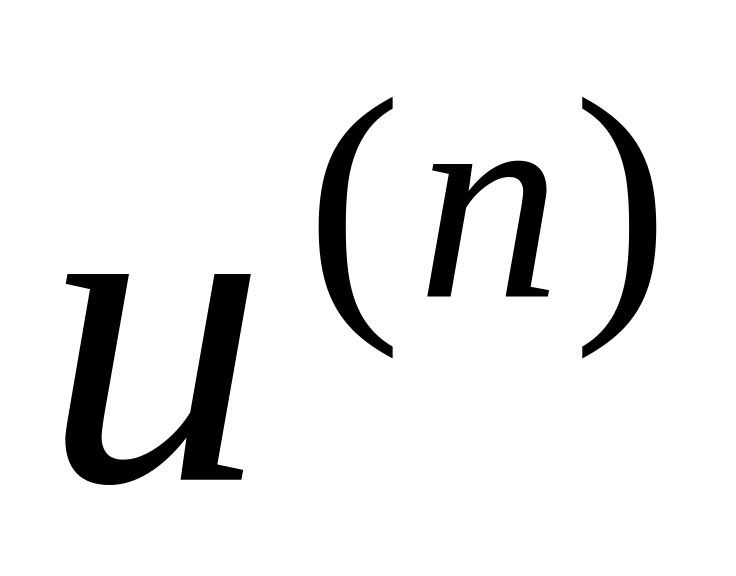
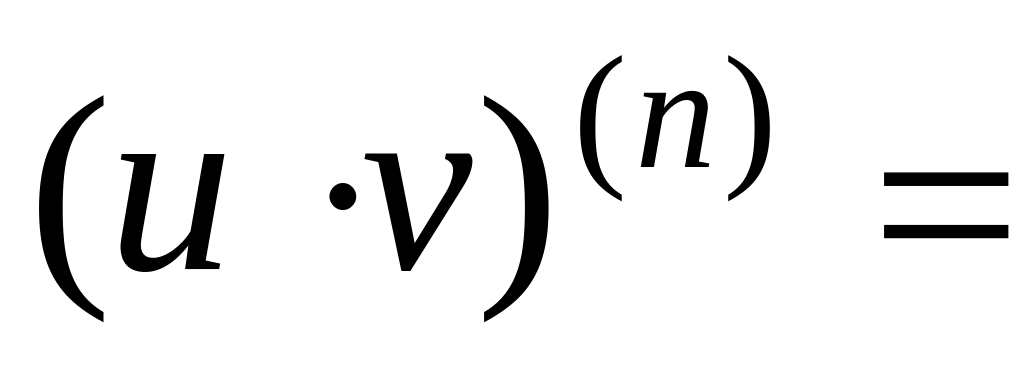
3. Формула Лейбніца. 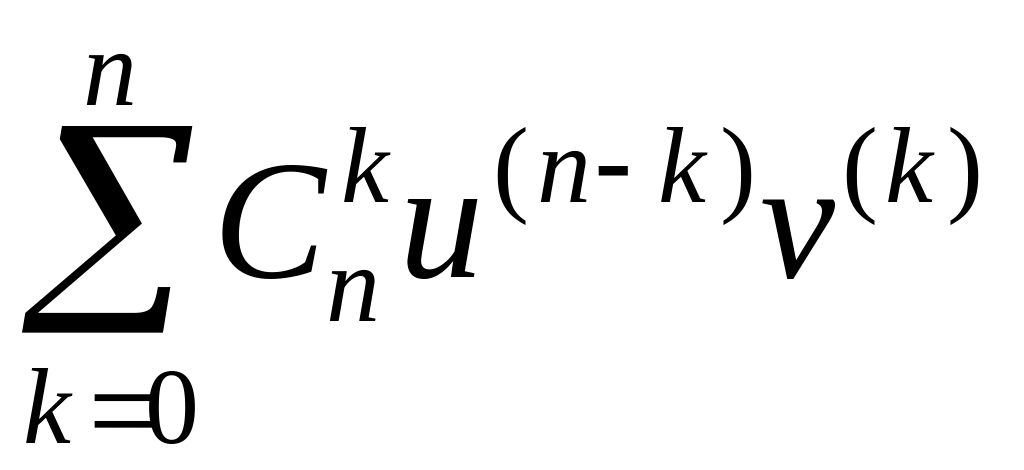, де .Дов. методом матем. індукції. =1 ( ).

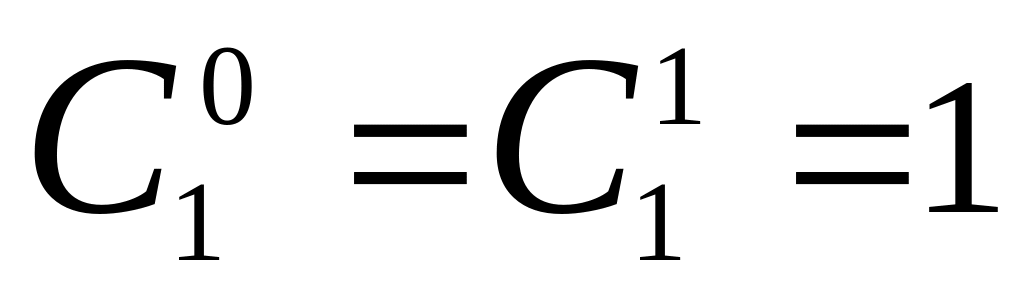=2 = . Припустимо, що формула вірна для = . Доведемо для = , = =

… … … … Доведено. Тут було використано , , .

4. = якщо -іррац. >0 то

5. =ln , то

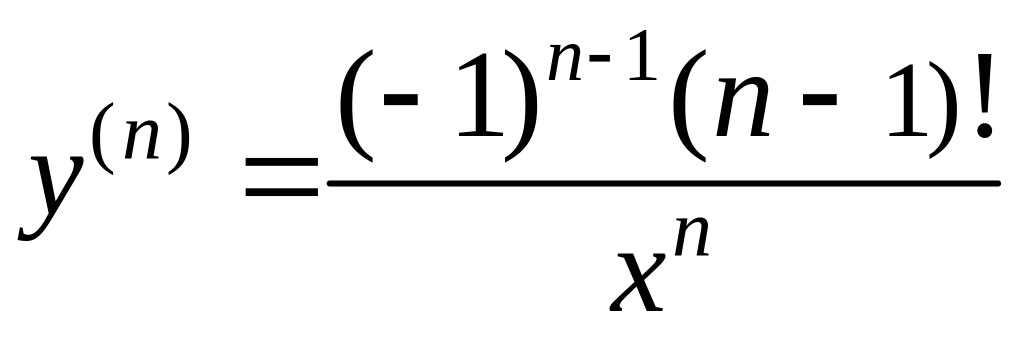
6. (cos) =cos( + ), (sin) =sin( + ).

Формули за якими обчислюються диференціали.

, … , , Дійсно,

Розглянемо випадок коли :