15. Формула Тейлора. Залишковий член у формі Пеано, Шльомільха-Роша,
Лагранжа, Коші.
Нехай
(1), де
має нескінченну кількість похідних.
;
, … ,
.Підставимо
у цих формулах
:
,
,
2
,…,
=
1
=
(2), підставимо ці коефіцієнти в (1):
+
+
+…+
(
).
Розкладемо по степенях
:
+
(
)
(
(3). Заміна
=
:
=
+
(4). Якщо
=0,
то маємо
=
,
=
,
… ,
=
(5). Підставимо (5) в (3):
=
+
(
)+…+
(
–
ф-ла
Тейлора для многочленна.
Формула Тейлора для довільної ф-ї.
Нехай
має
похідні до
-го
порядку включно в т.
.
=
+
(
)+
+…+
(1).
–
=
,
де
–залишок
після
-го
члена. Тому
=
+
=
+
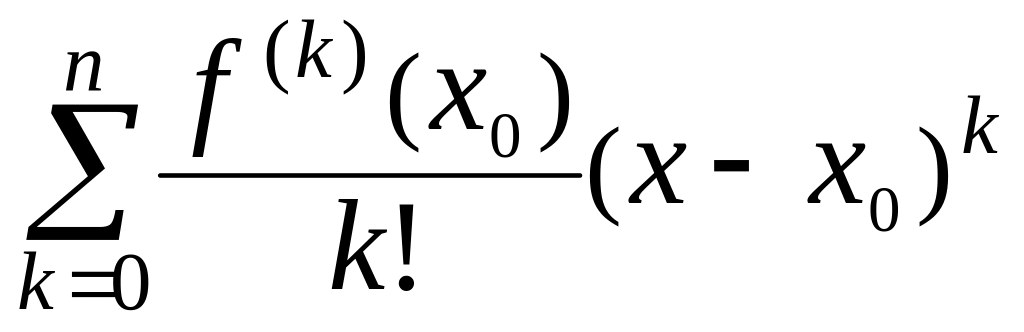.Якщо
=0,
то ф-лу
Тейлора наз. формулою Маклорена.
Залишковий
член у формі Пеано.
=о((
).
=
.
Теорема.
…
(3), то
=о(
).
Якщо (3) виконується то
є
нескінченно малою вищого порядку малості
ніж
,
то
=
о(
).
Дов.
Методом мат. індукції.Достатньо, щоб
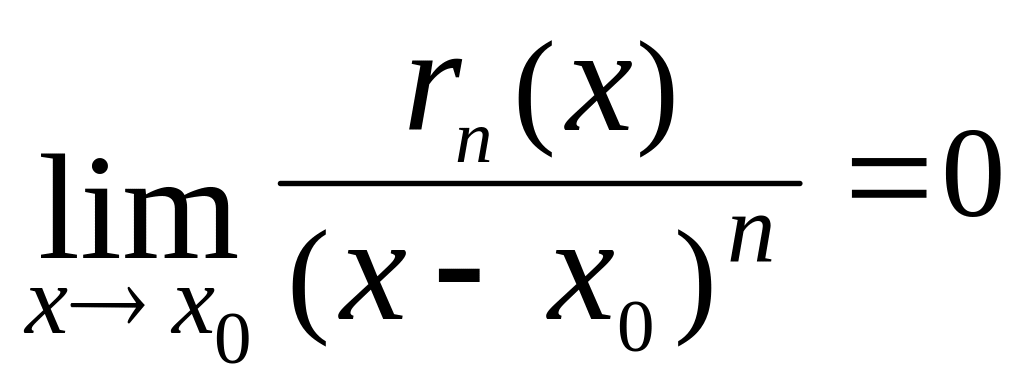.Розг.
=
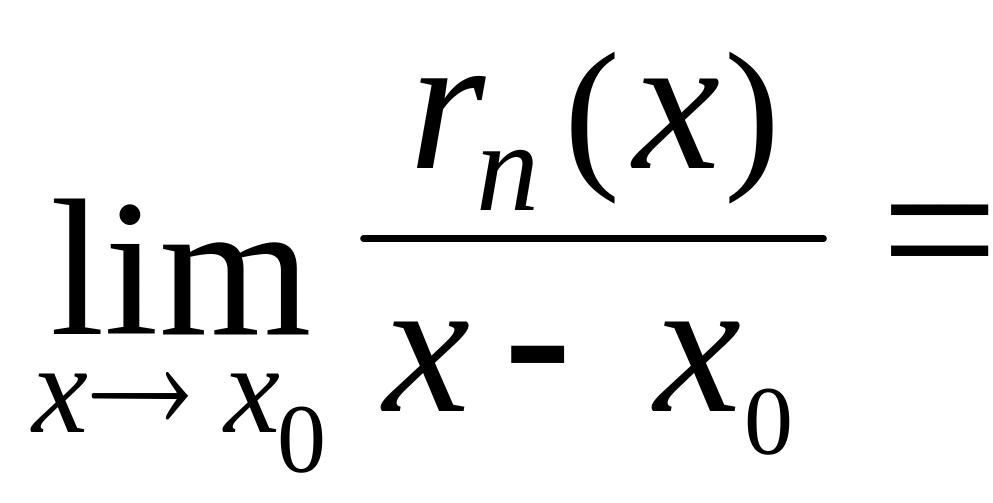
о(
).
Нехай викон. для
похідних.
Перевіримо
о(
),
маємо
о(
)
=о(
)
Дов
–но.
–загальна
формула для залишку. Підбираючи ф-ю
ми
отримаємо конкретну форму запису
залишку.
1. Форма
Шлемільха і Роша.
=
,
,
.
,
.
=
=
=
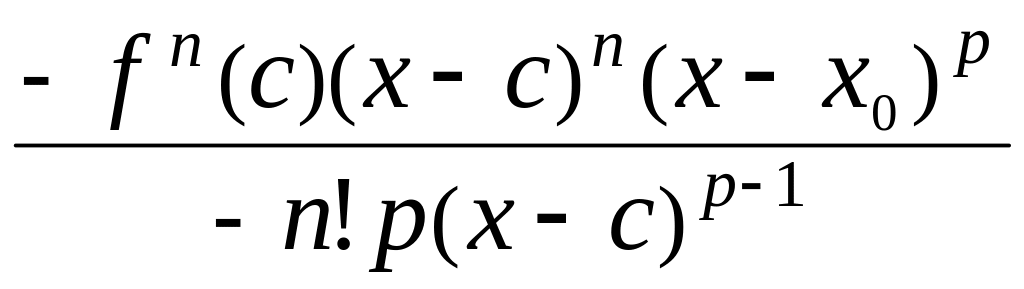2. Форма
Коші.
Коли
=
,
отримуємо
3. Форма
Лагранжа.
Коли
,
=
,
16.Необхідні і достатні умови сталості функції, монотонності функції.
Необхідні і достатні умови сталості функції.
Теорема.
Нехай
функція
визначена на проміжку X
і всередині цього проміжку має похідну
,
а на кінцях (якщо вони належать X)
зберігає неперервність. Для того,
щоб
функція f(x)
була тотожня константа в X
необхідно
і досить, щоб
=0
в середині X.
Дов.
Необхідність.
Нехай
тотожня
константа ,
.То
очевидно, що
.Необхідність
виконується.
Достатність.
Дано, що похідна у кожній точці дорівнює
нулю. Треба показати, що
тотожня
стала. Це означає, що які б ми дві точки
з області X
не взяли
.
Застосуємо
теорему Лагранжа.
.
=
=const.
Теорему доведено.
Наслідок.
Якщо
і
g(x)
визначені
на
проміжку
X
і всередині нього мають скінченні
похідні
і
,
ці похідні рівні, то ці функції
відрізняються на сталу
Дов.
Функція
-g(x)
має
похідну
.То
Необхідні і достатні умови монотонності функції у широкому розумінні.
Теорема.
Нехай
визначена на проміжку X
і всередині нього має скінченну похідну
.Для
того, щоб
була монотонно зростаючою (спадною) у
широкому розумінні необхідно і досить,
щоб
.
Дов.
Необхідність.
Нехай
неспадна (не зростаюча)
Застосуємо
теорему Лагранжа:
(1).Припустимо
що
Оскільки
і
,
то з (1)
.
. Аналогічно
для зростаючих.
Достатність.
Нехай
похідна для всіх x,
що міститься всередині X
,
тоді з формули (1)
видно,
що
.Тобто
функція не спадна. Теорему доведено.
Необхідні і достатні умови монотонності функції у вузькому розумінні.
Теорема. Нехай визначена на проміжку X і всередині нього має скінченну похідну . Для того, щоб була в X монотонно зростаючою (спадною) у вузькому розумінні необхідно і досить, щоб :
1)
;
2)
не утворюють інтервал, який повністю
міститься в X.
Дов.Необхідність.
1)Нехай
-
строго монотонно зростаюча для
. За попередньою теоремою
.
2) Від супротивного. Нехай
утворює інтервал
,який
повністю міститься в X.
Тоді візьмемо інтервал
і застосуємо на цьому інтервалі
теорему Лагранжа
.
Але всі
.
Тому
.
Звідси випливає, що функція
немонотонна у вузькому розумінні. Наше
припущення не вірне. Отже нулі похідної
не заповнюють інтервал
.
Достатність.
Нехай
виконується 1) і 2). В силу 1) ми маємо
-
монотонна у широкому розумінні. І нехай
вона немонотонна у вузькому розумінні,
тобто
,
який міститься в X,
що для всіх точок із
функція
.
То тут її похідна
.
І ці x
заповнюють
цілий інтервал
,
який повністю міститься в X.
Це суперечить 2). Тому функція монотонна
у вузькому розумінні. Теорему доведено.