- •11. Рівномірна неперервність.Теорема Кантора.Наслідок.
- •12. Похідна функції.Похідна композиції функцій, оберненої функції. Таблиця похідних. Похідна функції, заданої параметрично.
- •13. Диференціал. Інваріантність форми диференціала.
- •14. Похідні і диференціали вищих порядків.
- •15. Формула Тейлора. Залишковий член у формі Пеано, Шльомільха-Роша,
- •16.Необхідні і достатні умови сталості функції, монотонності функції.
- •17.Екстремум ф-ї. Необхідна умова, достатні умови.
- •18. Опуклість графіка функції. Необхідні і достатні умови випуклості. Точки перегину графіка функції. Умови існування.
- •19. Асимптоти графіка функції. Знаходження асимптот.
- •20. Первісна функція, властивості. Таблиця первісних.
- •21. Заміна змінної та інтегрування частинами.
- •22. Інтегрування раціональних функцій.
- •2.Прості дроби
- •3.Інтегрування правильних дробів
- •23.Означений інтеграл. Необхідна умова інтегровності. Необхідні і достатні умови інтегровності.
- •23.Означений інтеграл. Необхідна умова інтегровності. Необхідні і достатні умови інтегровності.
11. Рівномірна неперервність.Теорема Кантора.Наслідок.
Якщо
ф-ція
![]() визначена на деякому проміжку
визначена на деякому проміжку
![]() і неперервна в т.
і неперервна в т.![]() цього проміжку, то
цього проміжку, то
![]() або
або
![]() ,
що з
,
що з
![]() .
Припустимо, що ф-ція
.
Припустимо, що ф-ція
![]() непер. на всьому проміжку
,
тобто непер. в кожній т.
цього проміжку. Тоді для кожної т.
по заданому
непер. на всьому проміжку
,
тобто непер. в кожній т.
цього проміжку. Тоді для кожної т.
по заданому
![]()
![]() .
При зміні
в межах
,
навіть якщо
незмінюється, число
.
При зміні
в межах
,
навіть якщо
незмінюється, число
![]() буде мінятися. Тому постає питання : чи
можна вибрати одне
,
при заданому
,
яке б задовольняло усі
.
буде мінятися. Тому постає питання : чи
можна вибрати одне
,
при заданому
,
яке б задовольняло усі
.
рівномірно
непер. в обл.
,
якщо вона непер. в кожній точці обл.
і
![]() та
та
![]() ,
що
.
Отже, рівном. непер., це така непер., що
для всіх точок можна вибрати одне
.
,
що
.
Отже, рівном. непер., це така непер., що
для всіх точок можна вибрати одне
.
Т.
Кантора.
Якщо
визначена і непер. в замкнутому проміжку
![]() ,
то вона рівном. непер. на цьому пром.
,
то вона рівном. непер. на цьому пром.
Довед.(від
супрот.)
Припустимо, що
не рівном. непер. Тоді, яке б число
![]() не взяли, на проміжку
не взяли, на проміжку
![]() такі два значення
такі два значення
![]() і
і
![]() ,
що
,
що
![]() і
і
![]() .
Візьмемо послід.
.
Візьмемо послід.
![]() додатніх чисел так, щоб
додатніх чисел так, щоб
![]() .
Тоді для кожного
.
Тоді для кожного
![]() в
значення
в
значення
![]() і
і
![]() такі, що
такі, що
![]() і
і
![]() .
За лемою Больцано-Вейерштраса з обмеж.
послід.
.
За лемою Больцано-Вейерштраса з обмеж.
послід.
![]() можна виділити підпослід збіжну до
деякої т.
пром.
можна виділити підпослід збіжну до
деякої т.
пром.
![]() .
Тоді і сама послід.
збігається
до
.
Оскільки
.
Тоді і сама послід.
збігається
до
.
Оскільки
![]() ,
то одночасно і послід.
,
то одночасно і послід.
![]() збіг. до
.
Тоді в силу непер. ф-ції в т.
повинно бути
збіг. до
.
Тоді в силу непер. ф-ції в т.
повинно бути
![]() і
і
![]() так що
так що
![]() а це суперечить тому, що при всіх значеннях
а це суперечить тому, що при всіх значеннях
![]() .
.
Наслідок. Нехай ф-ція визначена і непер. у замкнутому пром. . Тоді , що якщо пром. довільно розбити на частинки з довжинами меншими , то в кожному з них коливання ф-ції буде менше .
12. Похідна функції.Похідна композиції функцій, оберненої функції. Таблиця похідних. Похідна функції, заданої параметрично.
Похідною даної функції наз. границя відношення приросту ф-ії до приросту незалежної змінної при довільному прямуванні цього приросту до нуля:
![]() (x)=
(x)=![]()
П-д. Нехай y=x.
Тоді
![]()
Теорема. Значення похідної (x) дорівнює тангенсу кута, утвореного з віссю Ох дотичної до графіка ф-ії y=f(x) у точці з абсцисою х.
Т.1. Похідна суми означеного скінченого числа функцій дорівнює сумі похідних доданків.
Т.2. Похідна добутку двох ф-ій дорівнює сумі добутків першої ф-ії на похідну другої і другої ф-ії на похідну першої.
Т.3. Похідна частки двох ф-ій дорівнює дробу, знаменник якого дорівнює квадрату дільника, а чисельник- різниці між добутком дільника на похідну діленого і добутком діленого на похідну дільника.
Тобто, якщо ми
маємо дві функції U(x)
і V(x)
диференційовані в т. х,
то буде диференційована їх сума, добуток
і частка(V(x)![]() 0)
1)
0)
1)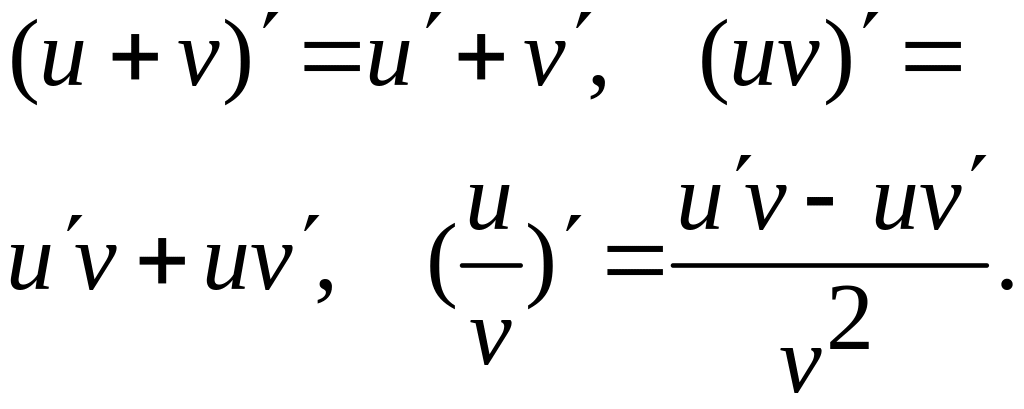
Похідна складної ф-ії дорівнює добутку похідних від ф-ій, які її складають.
Якщо функція в
точці х
має похідну, то вона називається
диференційованою
в цій точці. Похідна
оберненої функції.
Нехай маємо функцію y=f(x).
Нехай до неї існує обернена ф-ція
![]()
Теорема.1(?один
варіант?)Якщо
y=![]() -неперервна
ф-ія, яка обернена неперервній і має
похідну ф-ії y=f(x)
, то похідна
-неперервна
ф-ія, яка обернена неперервній і має
похідну ф-ії y=f(x)
, то похідна
![]() існує і значення її обернене за величиною
значенню
існує і значення її обернене за величиною
значенню
![]() при
при
![]() .
.
Теорема1(?другий
варіант?).
Якщо функція y=f(x)
в т. х має
похідну, не рівну нулю, то обернена ф-ція
у відповідній точці-у
також має похідну, яка записується:![]() або
або
![]() Доведення:1)
Надали приросту змінній у,
Доведення:1)
Надали приросту змінній у,
![]() 2)
Тоді змінна х набирає приріст
2)
Тоді змінна х набирає приріст![]() ,
,![]()
3)![]() ,
,
4)
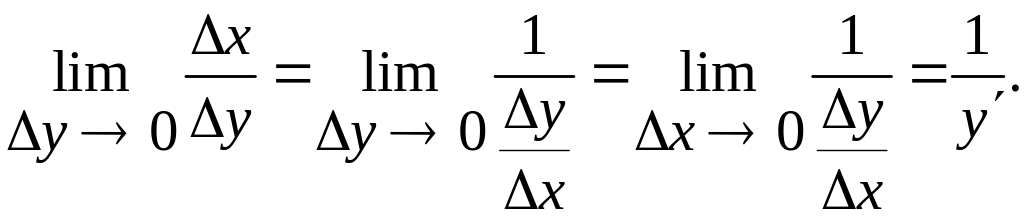
Отже
![]()
Похідна складної
функції.
Нехай y=f(u),
а
![]() ,
то ми маємо складну ф-цію:
,
то ми маємо складну ф-цію:
![]() .
.
Теорема2.
Якщо функція f(u)
має похідну
![]() ,
а ф-ція
,
а ф-ція
![]() має
похідну
має
похідну
![]() у
відповідній точці х, то складна ф-ція
має похідну
у
відповідній точці х, то складна ф-ція
має похідну
![]()
Доведення.
Поскільки існує
,
то існує границя
![]() при
при
![]() .
.
![]() Поділимо обидві частини на
і перейдемо до границі:
Поділимо обидві частини на
і перейдемо до границі:
![]() Якщо
Якщо
![]() ,
то
,
то
![]() Отже,
Отже,
![]() тобто
тобто
![]() .
.
Похідна ф-ції, заданої параметрично.
Теорема3. Якщо
ф-ції
![]() і
і
![]() мають
похідні
мають
похідні
![]() ,
причому
,
причому
![]() ,
тоді існує похідна
,
тоді існує похідна
![]() ,
рівна частці похідних. Доведення.
Якщо у- ф-ція від х, то
,
рівна частці похідних. Доведення.
Якщо у- ф-ція від х, то
![]()
Основна таблиця похідних: