
- •1. Декартів добуток множин. Відношення. Властивості бінарних відношень. Відношення еквівалентності. Відношення строгого і нестрогого порядку і зв’язок між ними.
- •2.Системи лінійних рівнянь
- •2.Системи лінійних рівнянь
- •3.Матриці і дії над ними. Обернена матриця. Матричний метод розв’язування систем лінійних рівнянь.
- •Нормальна форма матриці. Діагональна і жорданова форми матриць.
- •5. Многочлени, їх звідність. Ділення многочленів. Корені многочленів. Теорема Вієта.
- •6. Многочлен від багатьох змінних.Симетричні многочлени. Результант. Дискримінант.
- •7. Многочлени над числовими полями. Основна теорема теорії многочленів.
- •8. Лінійний простір. Приклади лінійних просторів. База, вимірність, інваріантність вимірності.
- •9.Лінійні оператори. Характеристичне рівняння, спектр, слід, мінімальний многочлен, власні значення і власні вектори лінійного оператора.
- •10. Лінійні оператори у евклідових і унітарних просторах. Ортогональні, унітарні, самоспряжені, нормальні оператори.
- •11. Квадратична форма. Додатньо і від’ємно визначені квадратичні форми. Закон інерції квадратичних форм. Критерій Сильвестра.
- •12. Зведення квадратичних форм до канонічного виду.
- •13. Поняття групи, підгрупи. Циклічні групи. Фактор-група.
- •14. Морфізми груп. Теорема про гомоморфізм груп. Ізоморфізм груп. Теорема Келі.
- •15. Поняття кільця, поля. Види кілець. Кільце квадратних матриць, кільце класів лишків, кільце многочленів.
- •16. Поле. Характеристика поля. Поле раціональних дробів. Побудова скінчених полів з допомогою фактор-кілець.
- •17 . Визначники. Ранг матриці
10. Лінійні оператори у евклідових і унітарних просторах. Ортогональні, унітарні, самоспряжені, нормальні оператори.
Озн евклідового простору.
L,R,
x,y Î
L
![]() (x,y)Î
R,
що називається їх скалярним добутком,
при цьому
(x,y)Î
R,
що називається їх скалярним добутком,
при цьому
1)(x,y)=(y,x)
2)(x,y+z)=(x,y)+(x,z)
3)(x,ly)= l(x,y)
4)(x,x)³0, (x,x)=0Þx=0, тоді простір L з заданим скалярним добутком є евклідовим простором.
Є два основні типи операторів у евклідових просторах: самоспряжені і ортогональні.
А:L L, А* називають спряженим до оператора А, якщо для довільних x,yÎL.(A(x),y)=(x,A(y)). Оператор А самоспряжений, якщо А=А*.А- самоспряжений, якщо в деякому ортонормованому базисі йому відповідає симетрична матриця.
Теорема про будову спряженого оператора:
Для довільного самоспряженого оператора можна вибрати ортонормований базис, що складається із власних векторів даного оператора.
Наслідок:Нехай А-квадратна матриця з дійсними елементами, якщо А- симетрична, то існує матриця Т з дійсними коефіцієнтами: Т-1АТ=D(діагональна).
Лінійний оператор А:L L називається ортогональним якщо для довільних x,yÎL.(A(x),А(y))=(x,y).
Квадратна матриця з дійсними елементами називається ортогональною, якщо АT=А-1
Теорема: Для А:L L (L- евклідовий простір) такі твердження еквівалентні:
1)А-ортогональний.
2)А переводить ортонормований базис в ортонормований.
3)В ортонормованому базисі оператору А відповідає ортогональна матриця.
Дов.
1Û2:Нехай А ортогональний оператор, а Б- ортонормований базис, оскільки А зберігає довжину і кут між векторами, то базис Б переводиться оператором А в ортонормований.
Навпаки: нехай Б=a1,..., an Б’=b1,...,bn=А(a1),..., А(an).
Треба довести,що А ортогональний.
x=a1 a1 +...+an an; y=b1 a1 +...+bn an.
(x,y)= a1b1+...+anbn
(A(x),A(y))=(a1b1+...+anbn, b1b1+...+bnbn)=a1b1+...+anbnÞ(A(x),A(y))=(x,y)
1Û3
А ортог.
Ûколи
для довільних x,y, (x,y)=(A(x),A(y)) Û(x,A*A(y))
Û
A*A=![]() ÛA*=A-1
ÛA*=A-1
A![]() A,
A*
AT,
A-1
A-1,
A-1=A*
Û
A-1=AT
Û
коли А - ортогональна.
A,
A*
AT,
A-1
A-1,
A-1=A*
Û
A-1=AT
Û
коли А - ортогональна.
Теорема про побудову ортогонального оператора.
Нехай А - ортогональний оператор. А:L L (L- евклідовий простір), тоді L=L1Å...Å Lk. dim Li=1 або 2. Якщо dim Li=1, то А діє на прямій Li як тотожний оператор або дзеркальне відображення. dimLi=2, то А діє на площині, як поворот на деякий кут j.
Наслідок: Для довільної ортогональної матриці А існує така ортогональна матриця Т:
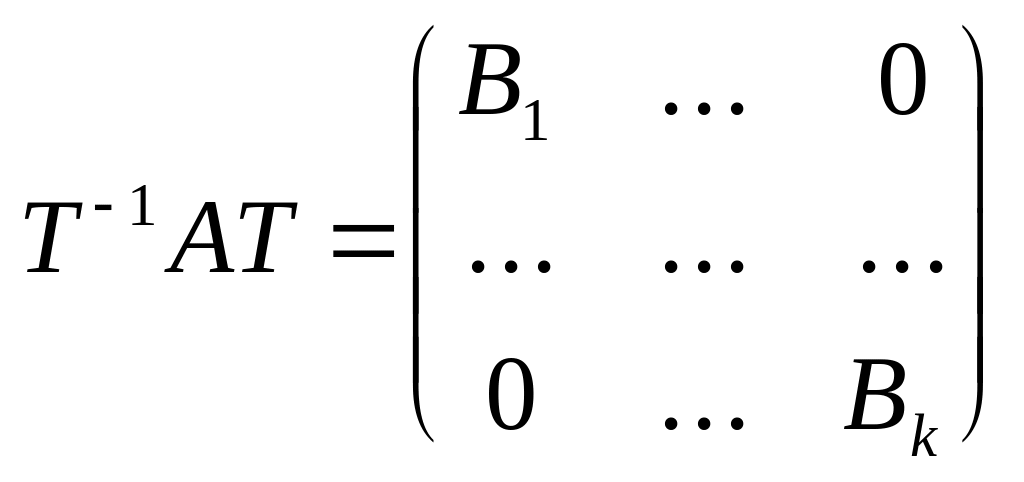 ,
де B1,...,
Bkклітини
розмірності 1 або 2.
,
де B1,...,
Bkклітини
розмірності 1 або 2.
Якщо
dimBi=1,
то Bi=I1.
Якщо dimBi=2,
то
![]() .
.
Теорема про будову невиродженого оператора на евклідовому просторі: Нехай А:L L,А - невироджений, тоді існують такі ортогональний оператор H і самоспряжений F: A=HF.
11. Квадратична форма. Додатньо і від’ємно визначені квадратичні форми. Закон інерції квадратичних форм. Критерій Сильвестра.
Квадратичною
формою
називається числова функція
![]() одного
векторного аргумента
,
яка випливає із білінійної форми
одного
векторного аргумента
,
яка випливає із білінійної форми
![]() ,
при
,
при
![]() .
.
Симетрична
білінійна форма
називається
полярною до квадратичної форми![]() .
.
Полярна
білінійна форма
![]() і
квадратична форма
зв’язані
наступним співвідношенням:
і
квадратична форма
зв’язані
наступним співвідношенням:
![]() ,
яке випливає з наступного співвідношення:
,
яке випливає з наступного співвідношення:
![]() і властивостей симетрії форми
.
і властивостей симетрії форми
.
Нехай
форма
в базисі
![]() визначається
матрицею
визначається
матрицею
![]() .
=
.
=![]() ,
де
,
де
![]() -
координати вектора
-
координати вектора
![]() в базисі
в базисі
![]() .
Припустимо, що дана форма може бути
приведена до канонічного вигляду
.
Припустимо, що дана форма може бути
приведена до канонічного вигляду
![]() ,
причому
,
причому
![]() шукаються за формулами:
шукаються за формулами:
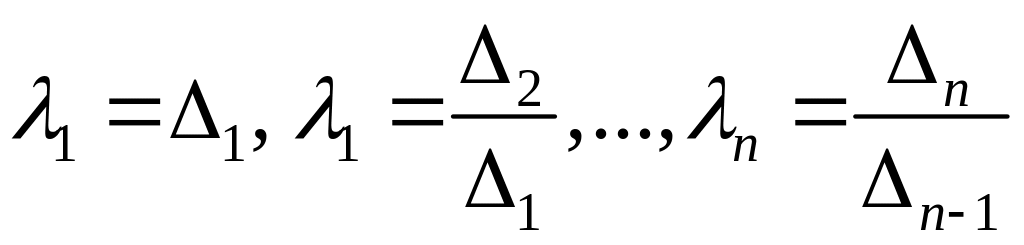 і занумеровані так, що перші
і занумеровані так, що перші
![]() є
додатними, а решту - від’ємними:
є
додатними, а решту - від’ємними:
![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() .
.
Нехай
![]() ,
,
![]() ,…,
,…,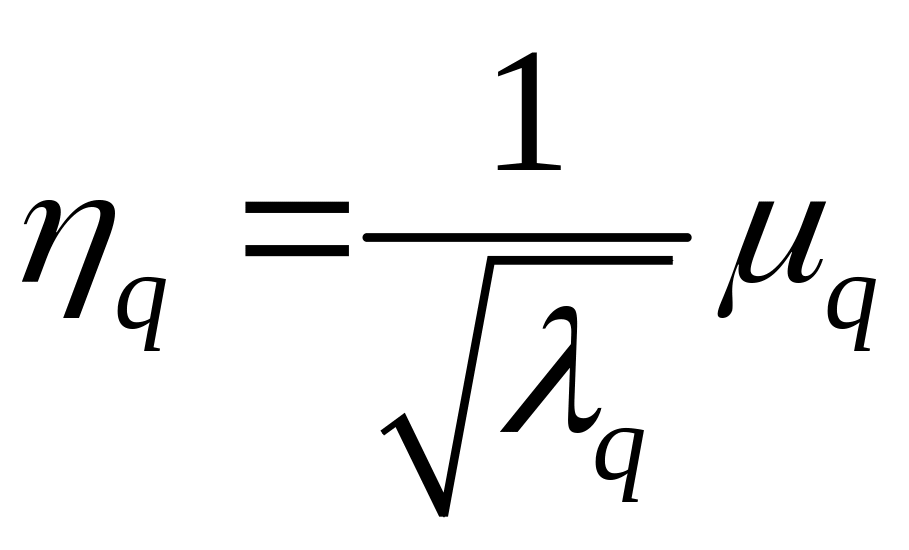 ,
,
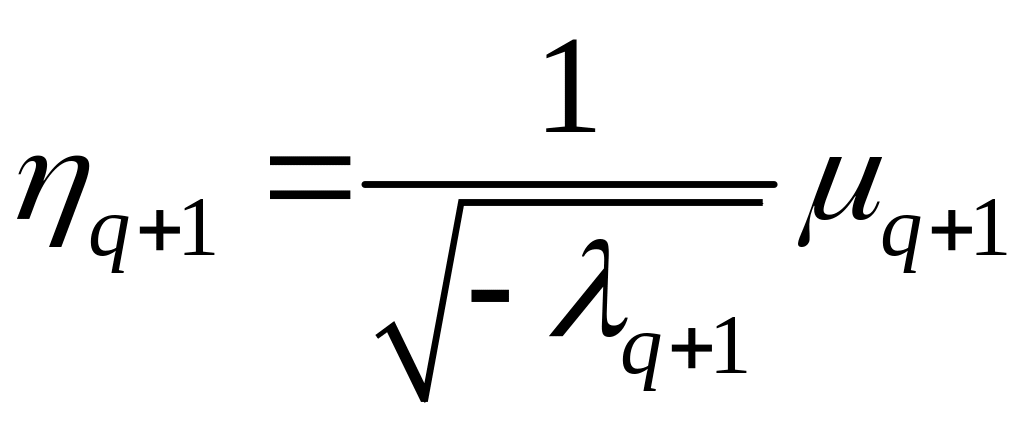 ,…,
,…,
![]() ,
,
![]() ,…,
,…,![]() .
В результаті отримаємо,
.
В результаті отримаємо,
![]() (*) , що наз. нормальним видом квадратичної
форми. Отже, з допомогою деякого
невиродженого перетворення координат
вектора
в базисі
(*) , що наз. нормальним видом квадратичної
форми. Отже, з допомогою деякого
невиродженого перетворення координат
вектора
в базисі
![]() ,
,
![]() (**) ,
(**) ,
![]() ,
,
![]() ,
квадратична форма приведена до нормального
вигляду.
,
квадратична форма приведена до нормального
вигляду.
Теорема1(закон
інерції квадратичної форми): Число
доданків з додатними (від’ємними)
коефіцієнтами в нормальному вигляді
квадратичної форми не залежить від
способу приведення форми до даного
вигляду.Доведення:
Нехай форма
з допомогою (**) приведена до (*), і з
допомогою другого не виродженого
перетворення координат прийдемо до
нормального вигляду
![]() (***) .Для доведення теореми потрібно
перевірити рівність
(***) .Для доведення теореми потрібно
перевірити рівність
![]() .Нехай
.Нехай
![]() .
Потрібно переконатися, що в даному
випадку існує ненульовий вектор
,
що по відношенням до базисів, в яких
форма має вигляд (*) і (***), координати
.
Потрібно переконатися, що в даному
випадку існує ненульовий вектор
,
що по відношенням до базисів, в яких
форма має вигляд (*) і (***), координати
![]() даного вектора рівні нулю:
даного вектора рівні нулю:
![]() (****).
Так як
(****).
Так як
![]() отримані шляхом не виродженого
перетворення (**) координат
,
а координати
отримані шляхом не виродженого
перетворення (**) координат
,
а координати
![]() з допомогою аналогічного не виродженого
перетворення тих же координат
,
то умову (****)можна розглядати як систему
лінійних однорідних рівнянь відносно
координат
шуканого вектора
в базисі
.Так
як
,
то число однорідних рівнянь (****) менше
n,
тому система (****) має ненульовий розв’язок
відносно
.
Тому, якщо
,
то існує ненульовий вектор
,
для якого виконується рівність (****).В
даному випадку отримаємо:
з допомогою аналогічного не виродженого
перетворення тих же координат
,
то умову (****)можна розглядати як систему
лінійних однорідних рівнянь відносно
координат
шуканого вектора
в базисі
.Так
як
,
то число однорідних рівнянь (****) менше
n,
тому система (****) має ненульовий розв’язок
відносно
.
Тому, якщо
,
то існує ненульовий вектор
,
для якого виконується рівність (****).В
даному випадку отримаємо:
![]() .Дана
рівність має місце, при
.Дана
рівність має місце, при
![]() і
і
![]() ,
що суперечить тому, що даний вектор є
ненульовим. Аналогічно, при
,
що суперечить тому, що даний вектор є
ненульовим. Аналогічно, при
![]() .Отже,
.Теорема доведена.
.Отже,
.Теорема доведена.
Квадратична
форма
називається: додатньо
(від’ємно) визначеною,
якщо для будь-якого ненульового
виконується рівність:![]()
![]() ;
знакозмінною, якщо існують такі
,
,
що
,
;
знакозмінною, якщо існують такі
,
,
що
,![]() .
.
Індексом інерції квадратичної форми наз. число відмінних від нуля канонічних коефіцієнтів даної форми; додатнім(від’ємним) індексом інерції- число додатних (від’ємних) канонічних коефіцієнтів.
Теорема2:
Для того, щоб квадратична форма
,
задана в
мірному
лінійному просторі, була знакосталою,
необхідно і досить щоб або додатній
індекс інерції
![]() ,
або від’ємний індекс інерції
були рівні розмірності
простору
.
,
або від’ємний індекс інерції
були рівні розмірності
простору
.
Якщо
![]() ,
то форма додатньо визначена, якщо
,
то форма додатньо визначена, якщо
![]() -
то від’ємно визначена.
-
то від’ємно визначена.
Доведення: Доведення проведемо для додатньо визначеної квадратичної форми. Для відємно визначеної квадратичної форми доведення проводиться аналогічно.
Необхідність:
Нехай
форма
додатньо визначена. Тоді
![]() .
Якщо
.
Якщо
![]() ,
то із останнього виразу випливає, що
для ненульового вектора
з координатами
,
то із останнього виразу випливає, що
для ненульового вектора
з координатами
![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() ,
форма
перетвориться в нуль, що суперечить
означенню квадратичної форми. Отже,
.
,
форма
перетвориться в нуль, що суперечить
означенню квадратичної форми. Отже,
.
Достатність:
Нехай
.
,
![]() ,
причому, якщо
,
причому, якщо
![]() ,
то
,
то
![]() ,
тобто
є нульовим. Відповідно,
є додатньо визначена квадратична форма.
Теорема доведена. Теорема3(Критерій
Сильвестра):
Для
того, щоб квадратична форма
,була
додатньо визначена необхідно і досить
щоб усі кутові мінори були додатними,
тобто
,
тобто
є нульовим. Відповідно,
є додатньо визначена квадратична форма.
Теорема доведена. Теорема3(Критерій
Сильвестра):
Для
того, щоб квадратична форма
,була
додатньо визначена необхідно і досить
щоб усі кутові мінори були додатними,
тобто
![]() ,
,
![]() ,…,
,…,![]() .
.
Для
того, щоб квадратична форма
,була
від’ємно визначена необхідно і досить
щоб знаки кутових мінорів чергувалися,
причому
![]() .
.
Доведення:
Необхідність: Докажемо
спочатку, що із умови
знакозмінності
квадратичної форми
випливає що
![]() ,
.Нехай
,
.Нехай
![]() .
Розглянемо квадратну однорідну систему
лінійних рівнянь:
.
Розглянемо квадратну однорідну систему
лінійних рівнянь:
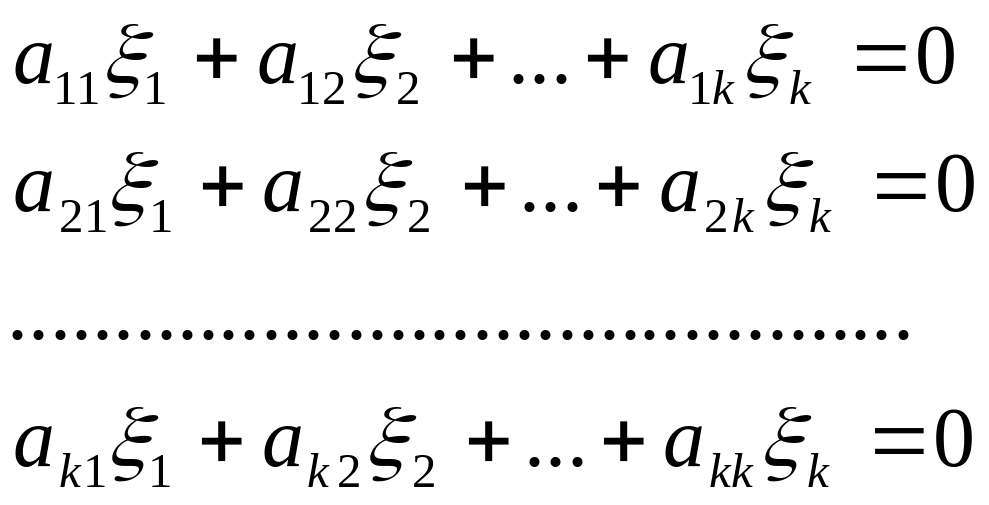 .
Так як
,
то система має ненульовий розв’язок
.
Так як
,
то система має ненульовий розв’язок
![]() (не
всі
(не
всі
![]() рівні 0).Помножимо перше з рівнянь на
рівні 0).Помножимо перше з рівнянь на
![]() ,
друге- на
,
друге- на
![]() ,…, останнє на
,…, останнє на
![]() .
В результаті отримаємо рівність
.
В результаті отримаємо рівність
![]() ,
ліва частина якого являє собою значення
квадратичної форми.
,
ліва частина якого являє собою значення
квадратичної форми.
![]() для ненульового вектора х
з
координатами
для ненульового вектора х
з
координатами
![]() .
Це значення рівне нулю що суперечить
знакозмінності форми. Якщо
– додотньо визначена форма. То всі
канонічні коефіцієнти додатні. З формул
для канонічних рівнянь випливає, що
,
,…,
.
Якщо ж
відємно визначена форма то всі канонічні
коефіцієнти від’ємні. Із означення
канон. коеф. випливає, що знаки кутових
мінорів чергуються, причому
.
.
Це значення рівне нулю що суперечить
знакозмінності форми. Якщо
– додотньо визначена форма. То всі
канонічні коефіцієнти додатні. З формул
для канонічних рівнянь випливає, що
,
,…,
.
Якщо ж
відємно визначена форма то всі канонічні
коефіцієнти від’ємні. Із означення
канон. коеф. випливає, що знаки кутових
мінорів чергуються, причому
.
Достатність.
Нехай
викон. умови накладені на кутові норми
![]() в формулюванні теор. Так як
в формулюванні теор. Так як
![]() і=1,2,3, …, п,
то форму А
можна привести до суми квадратів, причому
конон. коеф. шукаються за вказаними вище
формулами. Якщо
,
,…,
то з озн. канон. коеф. випливає що
і=1,2,3, …, п,
то форму А
можна привести до суми квадратів, причому
конон. коеф. шукаються за вказаними вище
формулами. Якщо
,
,…,
то з озн. канон. коеф. випливає що
![]() ,
тобто форма
додатньо визначена. Якщо ж знаки
чергуються і
,
тобто форма
додатньо визначена. Якщо ж знаки
чергуються і
![]() то форма
відємно визначена. Теорема доведена
то форма
відємно визначена. Теорема доведена
