1. Наближені величини. Абсолютна та відносна похибки. Гранична абсолютна і відносна похибки. Значущі цифри. Вірні значущі цифри. Звязок відносної похибки наближеного числа з кількістю вірних цифр цього числа.

Наближеною величиною наз величина, яка мало відрізняється від точної і заміняє її в обчисленні. Похибкою наближеного числа а наз величина а=а-А (або А-а). Якщо а>А, то кажуть, що а є наближенням до А з надлишком, якщо а<А, то це наближення з недостачею. Абсолютною похибкою називається величина =| a|=|a-A|. Граничною абсолютною похибкою наближеного числа а наз величина _а така, що |а-А| _а. Відносною похибкою наближеного числа наз величина . Граничною відносною похибкою наближеного числа а наз величина _а , така що _а . ; _а = ; _а=|a| _а. Якщо а>0: А=а(1 _а). Значущою цифрою числа наз будь-яка її відмінна від нуля цифра і нуль у двох випадках: 1. коли він міститься між значущими цифрами; 2. коли він є представником збереженого десяткового розряду. Вірною значущою цифрою наз така цифра, для якої абсолютна похибка заданого числа не перевищує половини одиниць розряду, в якому міститься ця цифра (вірність у вузькому сенсі). Вірною значущою цифрою наз така цифра, для якої абсолютна похибка заданого числа не перевищує одиниці розряду, в якому міститься ця цифра (вірність у широкому сенсі). Всі значущі цифри, які містяться лівіше від вірної цифри теж будуть вірними.

Теорема: Якщо число а зображене у вигляді: , де має n вірних цифр, то відносна похибка цього цисла задовольняє нерівність: .

Доведення: ; .

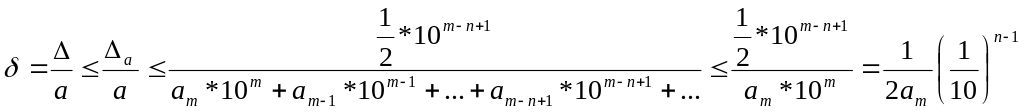2. Загальна формула для похибки. Похибки алг. суми, добутку, частки. Похибки обч. значень основних елем. ф-цій. Метод пол. поділу уточнення наближених значень коренів рівнянь: алгоритм, збіжність, оцінка наближення, блок-схема.

Маємо функцію . Припустимо, що кожна змінна має похибку . В якості похибки функції використовуємо приріст: . Припускаємо, що f-диференційована функція і скористаємося формулою: ; ; ; ; .

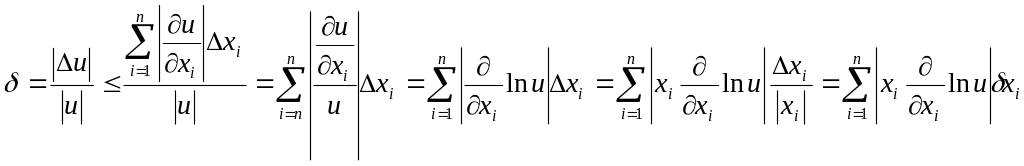Теорема про суму: Якщо всі х_і і=1,…, n одного знака, то відносна похибка функції u не перевищує відносної похибки найменш точного доданка. Доведення: ( ), і=1,…, n. Припустимо, що нам відомі . Знайдемо : ; ; .

Добуток: ; ; . Нехай , вважаємо, що кожен із співмножників х_і має m вірних цифр у вузькому сенсі. , де -старша значуща цифра числа . .Добуток буде мати (m-2) вірні цифри. Якщо співмножники беруться з різною кількістю вірних цифр, то в якості m беруть кількість вірних цифр у найменш точному співмножнику.

Частка: ; ; ; ; ; ; - в широкому і вузькому сенсі.

Похибки елементарних функцій: маємо функцію y=f(x) і похибки . ;

Табличка похибок:

Метод половинного поділу: Маємо відрізок [a;b]. f(a)*f(b)<0. Ділимо цей відрізок пополам. і . Провіряємо умову , якщо вона виконується, то тоді це є розв’язком рів-ня.Якщо ні, то розглядаємо дві половини відрізка і вибираємо ту, де функція приймає на кінцях різні значення ; <0. Знову провіряємо умову . Якщо виконується, то зупиняємося, якщо ні, то знову беремо ту половину відрізка, де ф-ція приймає значення різних знаків. І продовжуємо так далі. Приходимо до відрізка . В результаті маємо систему вкладених сегментів: . Збіжність: . Тобто дві послідовності збігаються до кореня рівняння. Оцінка: ; ; . Якщо будемо мати -точність наближення , то потрібно взяти таке n, щоб < , то .

Блок-схема:

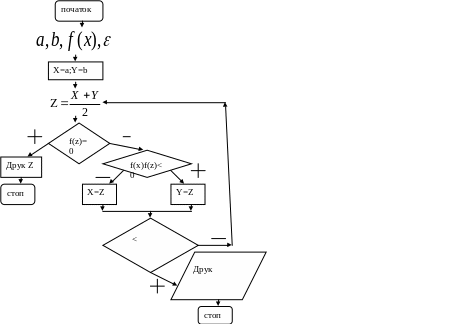
3. Метод хорд уточнення наближених значень коренів рівнянь: алгоритм, збіжність, оцінка наближення, блок-схема.

Нехай корені рів-ня f(x)=0 відокремлені на в-ку [a;b], причому ф-я f(x) двічі диф-на на інтер [a;b] і f^’(x), f^’’(x) 0 і зберігають свій знак на цьому пром-ку.

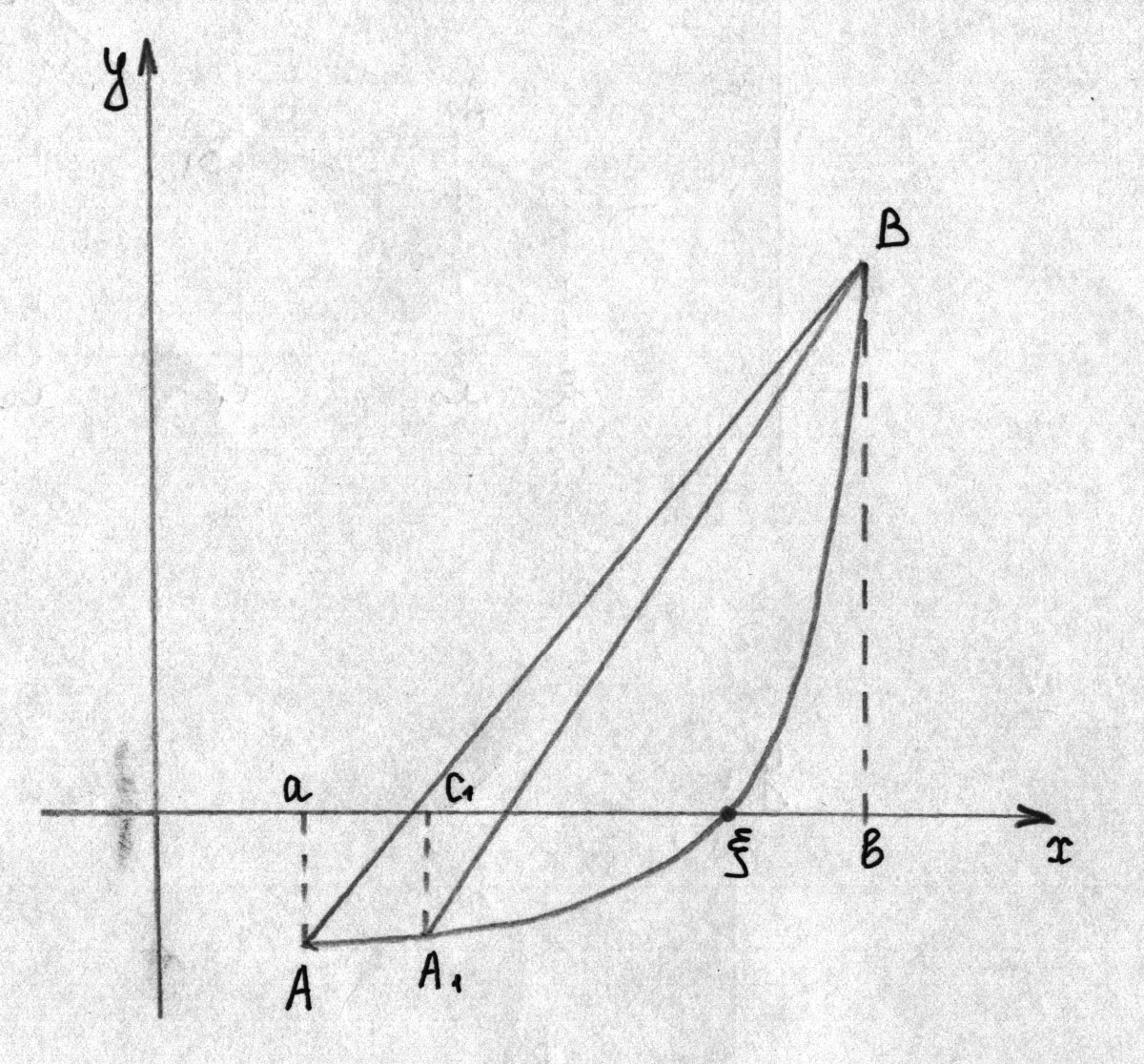
Суть методу хорд полягає в тому, що криву f(x)заміняємо хордою, яка з’єднує кінці відрізка, а наближеним значенням кореня будемо вважати точку перетину хорди з віссю Ох.

Розглянемо І тип кривої. Графік функції f(x) проходить через точки А(x₀, f(x₀)), В(b,f(b)). З’єднаємо точки а і b хордою АВ. Рівняння прямої, що проходить через 2 точки

. Підставимо у рівняння значення х=x₁, y=0, одержимо

Для знаходження координати точки x₂ будемо мати таке рівняння:

. Продовжуючи побудову хорд, одержимо . Розглянемо другий випадок, коли А(x₀, f(x₀)), В(b,f(b)). . Підставимо у рівняння значення х=x₁, y=0, одержимо , Для знаходження координати точки x₂ будемо мати таке рівняння:

Продовжуючи побудову хорд, одержимо .

Збіжність: (х_n)-монотонно зростаюча . Перейдемо до границі: . . . Оскільки , то .

Оцінюємо наближення: .

Оскільки , то додамо у ліву частину формули: . Застосуємо формулу Лагранжа для скінченних приростів: . .

. ,

. . Якщо ми кладемо, що , то при виконанні нерівності < , < , , , , < , < . Блок-схема:

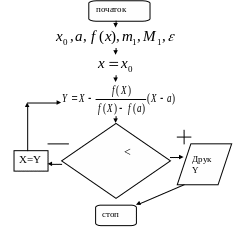
4. Метод дотичних (Ньютона) уточнення наближених значень коренів рівнянь: алгоритм, збіжність, оцінка наближення, блок-схема. Модифікація методу Ньютона.

Нехай ф-я f(x) двічі неперервно диф-на на в-ку [a;b], при чому f^’(x), f^’’(x) 0 і зберігає свій знак на цьому відрізку. Нехай корінь відокремлений на в-ку [a;b].

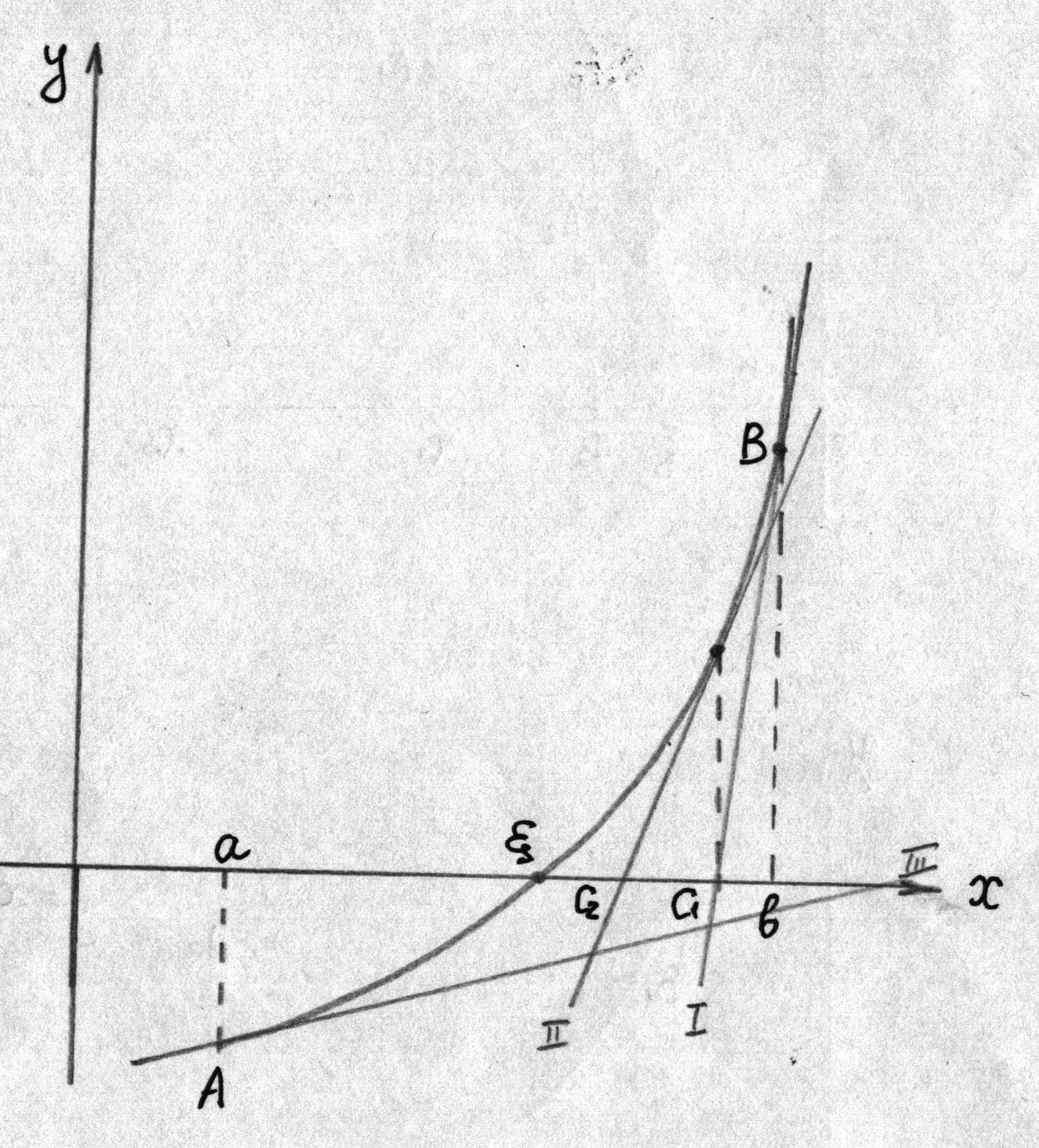
Суть методу дотичних полягає в тому, що криву у= f(x) заміняємо дотичною до цієї кривої, проведеної у кінцях відрізка. Точка перетину дотичної з віссю Ох вважається наближенням до розв’язку рівняння.

Проведемо дослідження методом дотичних на І типі кривої. Дотичну будемо проводити до кривої у= f(x) на тому кінці відрізка [a;b], де значення функції f(x) і 2-ї похідної f^’’(x) співпадають за знаком.

Для цього запишемо рівняння дотичної проведеної до графіка функції в точці (x₀,f(x₀)). у- f(x₀)= f’(x₀)(х-x₀). Позначимо координати першого наближення у=0, х=x₁.

- f(x₀)= f`(x₀)(x₁- x₀); . ; аналогічно продовжуємо так само: ; … … … .

Збіжність: , перейдемо до границі: , =0, , , , . , застосувавши формулу Лагранжа, отримаємо: , , , .

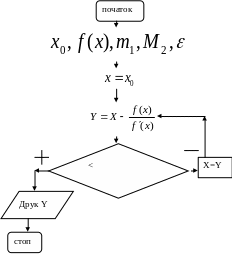
Оцінка наближення: Скористаємось формулою Тейлора: , , , , . Якщо < , то < . Блок-схема:

5. Метод ітерації уточнення наближених значень коренів рівнянь: ідея, збіжність, оцінка наближення, блок-схема. Зведення рівняння до вигляду, зручного для ітерацій.

Нехай задано рів-ня f(x)=0 при чому корінь цього р-ня відокремлений на в-ку [a;b], а ф-я f(x) неперервна на цьому відрізку. Замінимо дане рів-ня рів-ням , при чому функція неперервно диференційована на в-ку [a;b].

Суть методу ітерації полягає в тому, що ми вибираємо на відрізку [a;b] початкове наближення х₀. наступні наближення будемо обчислювати за рекурентною формулою х_n= (x_n-1), n=1,2,…

Збіжність: припускаємо, що . Перейдемо до границі: , .

Т: Нехай функція визначена, диференційовна і неперервна на відрізку [a;b]; ; | |≤q<1. Тоді послідовні наближення, що одержуються за методом ітерацій збігаються до кореня рівняння незалежно від вибору початкового наближення.

Д: , , , .

n=1 ; n=2 ; … … … n=k

Покажемо, що різниця , . Отже, .

Оцінка наближення: Оцінимо зверху різницю ? Для цього візьмемо таку різницю: , ; , підставивши n, отримаємо: , , … , , … ,

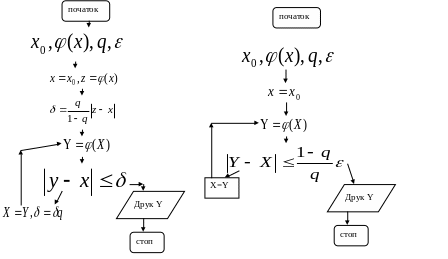
, , . Блок-схема:

Зведення рівняння: Завдання полягає в тому, щоб звести рівняння f(x)до вигляду .

1). . В нашому випадку , , . Щоб виконувалась рівність, візьмемо . Тоді , , <1, якщо .

2). >1, , , <1,

Геометричний зміст методу ітерацій

Побудуємо графіки функцій у=х і у= . Розглянемо 4 випадки:

І <1

II >1

III <-1

IV >-1

I Вибираємо точку х₀. х_n=φ(x_n-1) і отримаємо В₁, опускаємо перпендикуляр і отримаємо х₁. А₀(х₀,х₀), В₁(х₁, φ(x₁)), А₁(х₁,х₁), В₂(х₂, φ(x₂)), А₂(х₂,х₂), В₃(х₃, φ(x₃)).(Графік 1)

ІІ Вибираємо х₀, проведем вісь паралельну Оу, потім паралельну Ох – утвориться точка В₁. кореня немає, іде розбіжність. (Графік 2)

ІІІ Вибираємо точку х₀ ближче до ξ, піднімаємо перпендикуляр вверх – утвориться точка А₀. Горизонтально проводимо пряму – утвориться точка В₁, якій відповідає х₁. х₀, х₁, ..., х_n віддаляється від кореня – немає збіжності. (Графік 3)

IV Вибираємо х₀, піднімаємо перпендикуляр до перетину з прямою у=х. Це буде точка А₀. Проводимо паралельну осі Ох і утворилась точка В₁, опускаємо перпендикуляр – одержуємо х₁. х₀, х₁, ... послідовно наближуються до кореня. (Графік 4)