1. Уточнення наближених значень коренів рівняння f(x)=0 комбінованим методом хорд та дотичних. Геометрична ілюстрація. Блок-схема методу.

Метод хорд

Нехай корені рів-ня f(x)=0 відокремлені на в-ку [a;b], причому ф-я f(x) двічі диф-на на інтер [a;b] і f^’(x), f^’’(x)0 і зберігають свій знак на цьому пром-ку.

Суть методу хорд полягає в тому, що криву f(x)заміняємо хордою, яка з’єднує кінці відрізка, а наближеним значенням кореня будемо вважати точку перетину хорди з віссю Ох.

Розглянемо І тип кривої. Графік функції f(x) проходить через точки А(а, f(а)), В(b,f(b)). З’єднаємо точки а іbхордою АВ. Рівняння прямої, що проходить через 2 точки

.

Підставимо у рівняння значення х=с₁,y= f(с₁)=0, одержимо

=

Для побудови другої хорди опустимо перпендикуляр з точки на криву у= f^’(x), де утворилась точка А₁(,f()). Побудуємо хорду, з’єднавши точки А₁і В, с₂буде другим наближенням до кореня. Для знаходження координати точки с₂складемо рівняння прямої

.

О

Метод дотичних

скільки х=с₂, у=f(с₂)=0, то=. Продовжуючи побудову хорд, одержимо=.

Метод хорд

Метод дотичних

Нехай ф-я f(x) двічі неперервно диф-на на в-ку [a;b], при чому f^’(x), f^’’(x)0 і зберігає свій знак на цьому відрізку. Нехай корінь відокремлений на в-ку [a;b].

Суть методу дотичних полягає в тому, що криву у= f(x) заміняємо дотичною до цієї кривої, проведеної у кінцях відрізка. Точка перетину дотичної з віссю Ох вважається наближенням до розв’язку рівняння.

Проведемо дослідження методом дотичних на І типі кривої. Дотичну будемо проводити до кривої у= f(x) на тому кінці відрізка [a;b], де значення функції f(x) і 2-ї похідної f^’’(x) співпадають за знаком.

Позначимо точку перетину першої дотичної з віссю Ох с₁, яку будемо вважати першим наближенням до кореня. Знайдемо координату першого наближення. Для цього запишемо рівняння дотичної проведеної до графіка функції у= f(x) в точці В(b,f(b)).

у- f(b)= f`(b)(х- b)

Позначимо координати першого наближення у=0, х=с₁.

- f(b)= f`(b)(с₁- b)→.

Неперервний корінь рівняння знаходиться на відрізку [a;с₁]. Проведемо дотичну до графіка функції у правому кінці відрізка. Тоді формула знаходження другого наближення с₂ матиме вигляд

.

В результаті одержимо загальну формулу знаходження n–го наближення

.

Суть комбінованого методу хорд і дотичних полягає в тому, що з одного кінця ми будуємо хорди, а з другого дотичні. Цей метод має вищу швидкість збіжності ніж методи хорд і дотичних окремо взяті.

Малюнок №2

2. Уточнення наближених значень коренів рівняння f(x)=0 методом ітерацій. Геометрична ілюстрація. Блок-схема методу. Достатня умова збіжності методу ітерацій для рівнянь з одним невідомим. Оцінка похибки методу ітерацій для рівнянь з одним невідомим.

Нехай задано рів-ня f(x)=0 при чому корінь цього р-ня відокремлений на в-ку [a;b], а ф-я f(x) неперервна на цьому відрізку. Замінимо дане рів-ня рів-ням, при чому функціянеперервно диференційована на в-ку [a;b].

Суть методу ітерації полягає в тому, що ми вибираємо на відрізку [a;b] початкове наближення х₀. наступні наближення будемо обчислювати за рекурентною формулою х_n=(x_n-1), n=1,2,… Якщо послідовна наближеність {x_n}є збіжною, тобто має границю lim x_n=c, то це є коренем рівнянняf(x)=0, а також рівносильного йому рівняння. Дійсно с=limx_n=lim(x_n-1)=(limx_n-1)=(c). Збіжна послідовність {x_n} забезпечується вибором функціїта початковим наближенням х₀. якщо х₀вибрати ближче до кореня то швидкість збіжності підвищується, а вибираючи по різному функціюможна одержати різні ітераційні процеси знаходження кореня рівняння=0.

Достатні умови збіжності методу ітерацій:

Т: Нехай функція f(x) визначена і неперервна на відрізку [a;b]

||≤q<1. Всі послідовні наближенняx_n,які визначаються за рекурентною формулоюx_n=(x_n-1) не виходять за межі інтервала [a;b]. Тоді послідовна наближеністьx_nє збіжною, при чому границя послідовності є єдиним коренем рівняння f(x) = 0 і справджується оцінка

.

Геометричний зміст методу ітерацій

Побудуємо графіки функцій у=х і у=. Розглянемо 4 випадки:

І <1

II >1

III <-1

IV >-1

I Вибираємо точку х₀. х_n=φ(x_n-1) і отримаємо В₁, опускаємо перпендикуляр і отримаємо х₁. А₀(х₀,х₀), В₁(х₁,φ(x₁)), А₁(х₁,х₁), В₂(х₂,φ(x₂)), А₂(х₂,х₂), В₃(х₃,φ(x₃)).(Графік 1)

ІІ Вибираємо х₀, проведем вісь паралельну Оу, потім паралельну Ох – утвориться точка В₁. кореня немає, іде розбіжність. (Графік 2)

ІІІ Вибираємо точку х₀ближче до ξ, піднімаємо перпендикуляр вверх – утвориться точка А₀. Горизонтально проводимо пряму – утвориться точка В₁, якій відповідає х₁. х₀, х₁, ..., х_nвіддаляється від кореня – немає збіжності. (Графік 3)

IV Вибираємо х₀, піднімаємо перпендикуляр до перетину з прямою у=х. Це буде точка А₀. Проводимо паралельну осі Ох і утворилась точка В₁, опускаємо перпендикуляр – одержуємо х₁. х₀, х₁, ... послідовно наближуються до кореня. (Графік 4)

3. Класифікація методів роз-ня систем. Точні методи роз-ня систем лін. алгебраїчних р-нь(СЛАР). Роз-ня СЛАР методом Гауса та уточнення коренів, одержаних цим методом. Погано обумовлені с-ми р-нь.

Розглянемо систему з n рівнянь і n невідомих:

a₁₁x₁+ a₁₂x₂+…+ a_1nx_n=b₁

a₂₁x₁+ a₂₂x₂+…+ a_2nx_n=b₂ (1)

…

a_n1x₁+ a_n2x₂+…+ a_nnx_n=b_n.

Cистему (1) можна записати у вигляді:

, j=1,…,n , i=1,…,n

Розв’язком с-ми(1) називається упорядкований набір (с₁, с₂, ..., с_n) чисел, після підстановки яких в систему(1) кожне рівняння перетворюється у тотожність.

Методи розв’язання СЛАР можна поділити на: *Точні; *Наближені.

До точних методів належать метод Гаусса, метод квадратних коренів, метод Крамера, матричний метод.

Метод називається наближеним або ітераційним, якщо він дає змогу знайти наближений розв’язок системи(1) із наперед заданою точністю зі шляхом виконання скінченої кількості арифметичних операцій.

Метод Гаусса (метод послідовного виключення невідомих). За цим методом розв’язуємо СЛАР у два етапи:

• На першому етапі вихідну систему зводять до рівносильної їй системи східчастого вигляду. Цей процес перетворення називається прямим входом.

• На другому етапі, що називається зворотнім ходом знаходимо розв’язок одержаної системи.

a₁₁x₁+ a₁₂x₂+ a₁₃x₃=а₁₄

a₂₁x₁+ a₂₂x₂+ a₂₃x₃=а₂₄ (2)

a₃₁x₁+ a₃₂x₂+a₃₃x₃=а_34.

Припустимо, що система є сумісню і визначена, тобто ∆≠0. Нехай коефіцієнт а₁₁≠0, тоді виключимо змінну х₁із 2-го і 3-го рівняння системи (2). Для цього перше рівняння поділимо на коефіцієнт a₁₁, одержимо:

х₁+а₁₂⁽¹⁾х₂+ а₁₃⁽¹⁾х₃= а₁₄⁽¹⁾, де,j=2,3,4.

Верхній індекс означає порядок перетворення рівняння. Домножимо перше рівняння на а_і1і віднімемо його від 2-го і 3-го рівняння відповідно. В результаті одержимо систему 2-х рівнянь:

а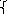₂₂⁽¹⁾х₂+ а₂₃⁽¹⁾х₃= а₂₄⁽¹⁾

а₃₂⁽¹⁾х₂+ а₃₃⁽¹⁾х₃= а₃₄⁽¹⁾, де а_ij⁽¹⁾=a_ij-a_1j⁽¹⁾a_i1, i,j=2,3,4. (3)

Виконаємо аналогічні перетворення із системою (3). Поділимо перше рівняння на а₂₂⁽¹⁾

х₂+ а₂₃⁽²⁾х₃= а₂₄⁽²⁾, де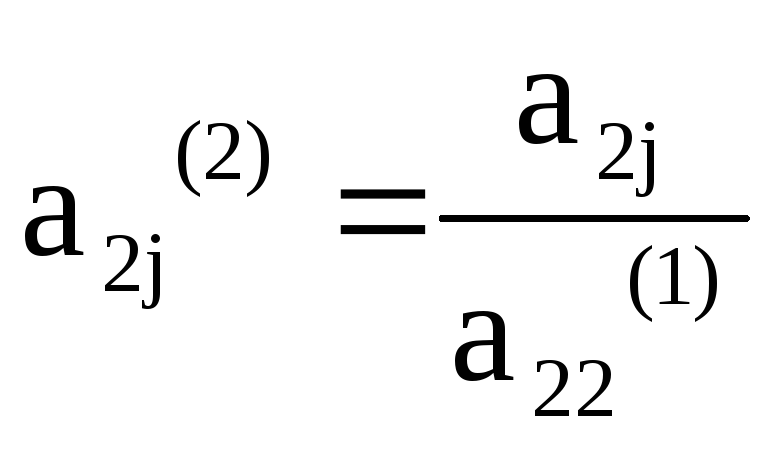,j=3,4.

Виключимо х₂з 2-го рівняння системи (3): помножимо одержане рівняння на а₃₂⁽¹⁾і віднімемо від 2-го рівняння:

сх₃= а₃₄⁽²⁾, а_3j⁽²⁾=a_3j⁽²⁾-a_2j⁽¹⁾a₃₂⁽¹⁾,j=3,4.

Знайдемо х₃ з останнього рівняння:

х₃=а₃₄⁽³⁾,

В результаті одержимо систему східчастого вигляду:

х₁+а₁₂⁽¹⁾х₂+ а₁₃⁽¹⁾х₃= а₁₄⁽¹⁾,

х₂+ а₂₃⁽²⁾х₃= а₂₄⁽²⁾, (4)

х₃=а₃₄⁽³⁾.

Система (4) рівносильна системі (2), оскільки ми використали елементарні перетворення рівнянь. Прямий хід завершено, при чому елементарні перетворення можна виконати, якщо a₁₁≠0, а₂₂⁽¹⁾≠0, а₃₃⁽²⁾≠0.

4. Розв’язування систем алгебраїчних рівнянь методом ітерацій. Достатня умова збіжності методу ітерацій для систем алгебраїчних рівнянь та оцінка похибки методу

Метод простої ітерації.Розглянемо с-му зnрівнянь зnневідомими:

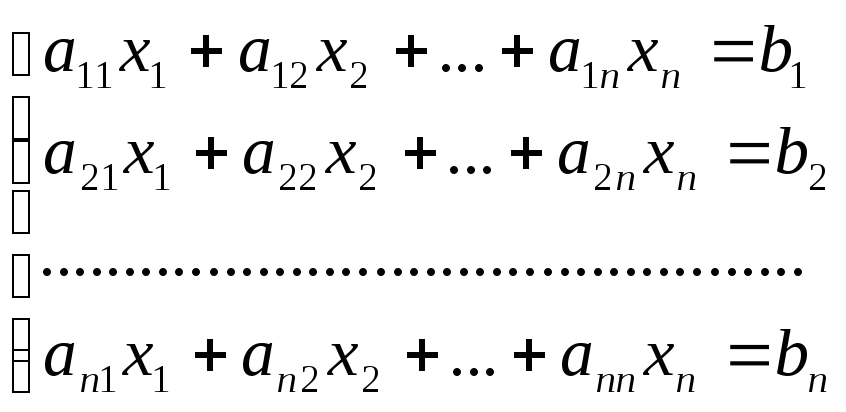(1)

Представимо с-му у матричному вигляді: A= (2)

Нехай всі елементи (і=) матриці А відмінні від 0. Залишимо в лівій частині р-ня с-ми діагональні елементи і кожне р-ня поділимо наодержимо:

Запишемо с-му у матричній формі:

(- це вектор стовпець) (3)

α=

С-му (3) наз. зведеною с-мою послідовного наближення для відшукання розв. с-ми (3) будують за формулами:

(4)

За початкові наближення , як правило обирають вільні члени. Якщо послідовністьє збіжною, то границяє розв. с-ми (3).

Праву частину с-ми (3) можна розглядати, як деяке відображення. Оператор φ, який відображає вектор вn-вимірному просторі у вектор, який визначається за формулою:. Тоді відшукання розв.с-ми (3) зводиться до відшукання нерухомої точки відображення φ. (Нерух. т.). Якщо відображення φ є стискуючим, то розв. р-няможна знайти за методом послідовних наближень з довільним поч. вектором. Розглянемо випадки при яких відображення φ буде стискуючим. Поняття стискуючого оператора залежить від самого оператора, а також від вибору метрикиn-вимірного простору.Розглянемо 3 випадки вибору метрики:

1.Нехай відстань між векторами івизнач. за формулою:

Знайдемо

Отже, оператор φ буде стикуючим, коли ,(5)

Якщо <1,то з принципу стискуючих відображень р-ня (3) має єдиний корінь.

2. Нехай метрику введемо за формулами:

Відображення φ буде стискуючим, якщо викон. нер-сть:

(6)

Якщо ум(6) викон.,то за прин-м стискуючого відоб-ня(3) буде мати єдин.розв.

3. Визначимо відстань між таза допомогою формули:

(7)

Якщо умова (7) викон. , то відобр. φ є стискаючим і за принципом стискаючого відображення р-ня (3) має єдиний корінь.

Т1.Якщо матриця α с-ми р-нь (3) задовольняє одну з умов (5)-(7) (0<l₁<1, 0<l₂<1, 0<l₃<1), то с-ма (3) має єдиний розвязок, який можна знайти, як границю, побудованої за допомогою рекурентних формул (4) почин. з довільного поч. наближення.

Т2.Якщо елементи матриці А задов. одну з умов:

,,, то с-ма р-нь (1) має єдиний розв., який можна одержати, як границю послідовностіпобудованої за формулами:

Починаючи з довільного початкового наближення .

Оцінка похибкиметоду простої ітерації визнач ф-лою:, девизнач. за формулою (5), (6), (7).

5. Розв’язування систем нелінійних рівнянь методом Ньютона.

Нехай дано с-му 2-ох нелінійних р-нь:

Нехай відомо kнаближень, тоді за більш точні їхні значення можна прийняти:

тоді с-ма буде мати вигляд:

Розкладемо ф-ції f і φ у ряд Тейлора по степенях і:

де імістять величини вищого порядку малості, ніжі. Підставимо ці ф-ції у с-му обмежившись доданками, які є лінійними що доі.

Перенесемо знач ф-ції у праву сторону:

Знайдемо величини із останньої с-ми викор. метод Крамара:

(12)

(13)

Отже послідовні наближення за методом Ньютона шукаєм за ф-лами:

де івизнач. за ф-лами (12) і (13), а поч. наближеннявибираються за допомогою графіків.