Прямые отображения
Прямым отображением 1-го порядка
вершины хi является
множество таких вершин графа, для которых
существует дуга (хi, xj),
т. е
(
хi ) = {xj :
дуга (хi, xj)
A} для графа G
= (X, A), где
X ={ хi }, i
=1, 2, ..., n – множество
вершин, а A = {ai},
i = = 1, 2, ..., m
– множество дуг.
Прямое отображение 2-го порядка
вершины хi – это прямое
отображение от прямого отображения
1-го порядка, т. е.
( хi ) =
( Г+1 ( хi ) ).
Аналогично можно записать для прямого отображения 3-го и т. д. n-го порядка.
(xi)= ( (xi))= ( ( (xi)))
...
(xi)=
(
(xi)).
Рис. 3.1. Орграф G
Прямые многозначные отображения для графа на рис. 3.1 находятся следующим образом:
(x1)=(x2,x3),
(x1)= (Г+1(x1))= (x2,x3)=(x3,x5),
(x1)= ( (x1))= (x3,x5)=(x3,x1) и т. д.
Обратные отображения
Обратным отображением 1-го порядка для вершины хiявляется множество элементов xjтаких, что существует дуга(xj, хi), принадлежащая множеству дуг графа, т. е. (хi ) = { xj : дуга (хj, хi) А }.
Обратные отображения 2-го, 3-го и т. д. n-го порядка определяются следующим образом:
(xi)=
(
(xi)),
(xi)= ( (xi)),
...
(xi)=
(
(xi)).
Для графа на рис. 3.1 обратные многозначные отображения вершины х1 находятся следующим образом:
(x1)=x5,
(x1)= ( (x1))= (x5)= x2,x4,
(x1)= ( (x1))= (x2x4)= x1,
(x1)= ( (x1))= (x1)= x5 и т.д.
П р и м е ч а н и я:
1. Когда отображение действует не на одну вершину, а на множество вершин Хq = { х1, х2, ..., хq }, то под Г(Хq) понимают объединение
Г(х1) Г(х2) ... Г(хq).
2. Многозначное отображение для неориентированного графа строится, если представить каждое ребро двумя противоположно направленными дугами (рис. 3.2).
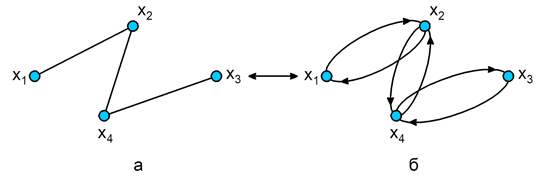
Рис. 3.2. Граф: а – неориентированный; б – тождественный ему ориентированный
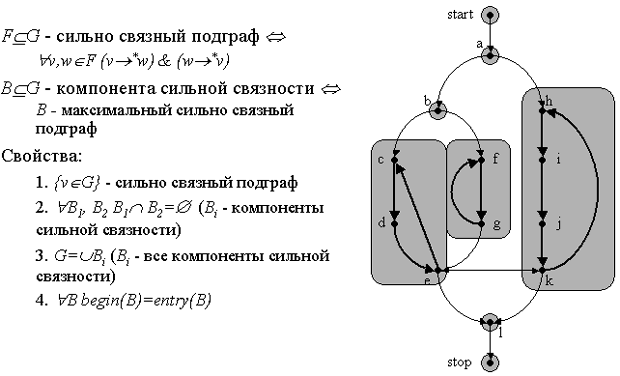
Сильно связный подграф - это фрагмент, состоящий из взаимно достижимых вершин. Компонента сильной связности - это максимальный сильно связный подграф.
Очевидно, произвольная вершина является сильно связным подграфом. Кроме того, легко показать, что множество компонент сильной связности задает разбиение множества вершин. Это разбиение показано на слайде.
Наконец, множества входных и начальных вершин для компонент сильной связности совпадают.