9. Неперервні ланцюги Маркова. Рівняння Колмогорова.

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова. При условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

В экономике часто случаются ситуации, которые заранее указать невозможно. Например, любая деталь или агрегат автомобиля могут выйти из строя в непредсказуемый момент времени.

Пусть система характеризуется n состояниями: S₀, S₁, S₂, …, S_n, а переход из состояния в состояние может осуществляться в любой момент времени t. Обозначим через P_i(t) вероятность того, что в момент времени t система будет находиться в состоянии S_i. Требуется определить для любого момента времени t вероятности состояний P₀(t), P₁(t), …, P_n(t). Очевидно, что сумма всех этих P_i .

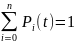Для процесса с непрерывным временем вместо переходных вероятностей P_ij(t) рассматриваются плотности вероятности перехода λ_ij(t), которые представляют собой отношение вероятности перехода системы за время Δt из состояния S_i в S_j состояние к длине промежутка Δt.

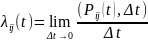
Где P_ij(t, Δt) – вероятность того, что система, пребывавшая в момент времени t в состоянии S_i, за промежуток времени Δt перейдёт в состояние S_j. Если λ_ij=const, то процесс называется оборотным. Если λ_ij=λ_ij(t), то процесс называется неоднородным.

Вероятности состояний P_i(t) находят путём решения системы ДУ Колмогорова.

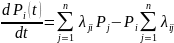(1)

Величина λ_ijP_i называется потоком вероятности перехода системы из состояния S_i в состояние S_j, причём интенсивность потока λ_ij может быть или постоянной, или зависящей от времени. i=0, …, n. Уравнение (1) составляют, пользуясь следующим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное состояние, минус сумма всех потоков, идущих из данного состояния.

Финальные вероятности состояний.

Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятности P_i(t), когда t→∞; .

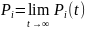Финальные вероятности состояний (если они существуют) могут быть получены путём решения системы линейных алгебраических уравнений, которые получаются из ДУ Колмогорова, если в них приравняем производные 0.

Пример. Имеется граф Маркова. Необходимо составить систему ДУ Колмогорова и записать начальные условия для решения этой системы, если известно, что в начальный момент система находилась в состоянии s₁.

Таким образом, согласно приведенному правилу, система ДУ Колмогорова принимает вид:

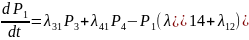
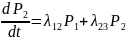
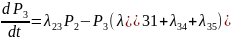
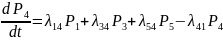
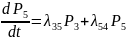
P₁(0)=1, P₂(0)= P₃(0)=…= P₅(0)=0.

Финальные вероятности не зависят от времени, поэтому в системе ДУ Колмогорова все левые части принимают равными нулю и система ДУ превратится в систему алгебраических уравнений.

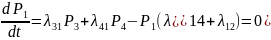
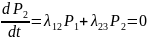
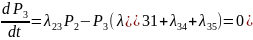
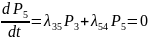
Решая её вместе с условием P₁+P₂+P₃+P₄+P₅=1 и получаем предельные вероятности.