17. Необхідні й достатні умови ідентифікованості. Перша і друга умова ідентифікованості.

Маючи дві форми системи одночасних рівнянь, необхідно визначити, яка з них краще підходить для оцінювання параметрів моделі. Передусім необхідно дослідити можливість застосування звичайного метода найменших квадратів до окремих рівнянь системи. Щоб забезпечити необхідну якість оцінок параметру, а саме незміщеність, ефективність, намагаються на підставі оцінених параметрів зведеної форми отримати оцінки параметрів структурної форми. Щоб передбачити можливі варіанти розв’язання задачі оцінювання параметрів системи одночасних рівнянь, необхідно попередньо оцінити ідентифікованість системи. Під проблемою ідентифікованості розуміють можливість чисельної оцінки параметрів структурних рівнянь за оцінками коефіцієнтів зведених рівнянь.

Економетрична модель, яка задана системою одночасних рівнянь, називається точно (строго) ідентифікованою, якщо одночасно можна отримати оцінки її параметрів на основі оцінених параметрів зведеної моделі.

Надідентифікованою називається така модель, що для деяких її параметрів можна отримати кілька кількісних значень параметрів структурної моделі, на основі заданих параметрів зведеної форми.

Нехай система одночасних рівнянь містить N рівнянь відносно N ендогенних змінних, а також M екзогенних змінних. Крім того, для деякого рівняння кількість ендогенних і екзогенних змінних у перевірці на ідентифікованість становлять n і m змінних.

Змінні, що не входять в дане рівняння, а входять в інші рівняння, називають виключеними. Їх кількість дорівнює (N-n) і (M-m).

Рівняння є ідентифікованим, якщо воно включає (N-1) змінну (ендогенну або екзогенну), що присутня в моделі. Тобто, (N-n)+(M-m)≥N-1. Перша необхідна умова ідентифікованості.

Друга умова ідентифікованості. Рівняння ідентифіковане, якщо кількість виключених з нього екзогенних змінних не менше кількості ендогенних змінних в цьому рівнянні, зменшеній на одиницю. M-m ≥ n-1.

Знаки рівності в обох необхідних умовах відповідають точній ідентифікованості.

Необхідна і достатня умови ідентифікованості.

В моделі, що містить N рівнянь відносно N ендогенних змінних, умова ідентифікованості виконується тоді і тільки тоді, коли ранг матриці, складеної з виключених з даних рівнянь змінних, але таких, що містяться в інших рівняннях, дорівнює N-1.

12. Приклад розрахунку роботи автопідприємства за допомогою ланцюгів Маркова

Представим автомобиль как некоторую систему S с дискретными состояниями S₀, S₁ … S_n, которая переходит из состояния в состояние под влиянием случайных событий (отказов).

На стадии прогнозирования (планирования) работы автомобиля целесообразно рассматривать следующие состояния, в которых подвижной состав может находиться в процессе эксплуатации и которые характеризуются целодневными простоями:

S₀ – исправен, работает;

S₁ – находится на капитальном ремонте (КР);

S₂ – проходит ТО-2;

S₃ – находится в текущем ремонте (ТР);

S₄ – исправен, не работает по организационным причинам (без водителя, шин, запасных частей);

S₅ – не работает, снятие агрегата для отправки на КР;

S₆ – не работает, списание агрегата, замена на новый;

S₇ – исправен, не работает (выходные и праздничные дни);

S₈ – списывается.

Надо отметить, что в настоящее время вышеперечисленные состояния автомобиля планируются при разработке годовой программы работы автотранспортного предприятия (АТП), при этом состояния S₃, S₅, S₆ объединяются в одно состояние «находится в ТР».

Для анализа процесса эксплуатации автомобиля как случайного процесса с дискретными состояниями удобно воспользоваться геометрической схемой, так называемым графом состояний. Граф состояний изображает возможные состояния автомобиля и его возможные переходы из состояния в состояние.

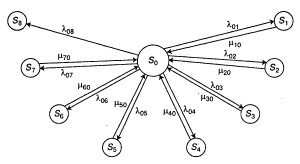
Через λ_ij и μ_ij обозначены плотности вероятностей перехода автомобиля из состояния S_i в состояние S_j.

Можно считать, что события, переводящие автомобиль из состояния в состояние, представляют собой потоки событий (потоки отказов). Если все потоки событий, переводящие систему (автомобиль) из состояния в состояние, пуассоновские (стационарные или нестационарные), то процесс, протекающий в системе, будет марковским, а плотности вероятности перехода λ_ij в непрерывной цепи Маркова представляют собой интенсивности потока событий, переводящего систему из состояния S_i в состояние S_j.

Рассматриваемые состояния автомобиля S_j характеризуются средним числом дней пребывания автомобиля в каждом состоянии Д_j. Показатели Д_j находят отражение в статистической отчетности АТП. Отношение 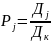, где Д_к – число календарных дней в году.

Д_к можно трактовать как вероятность нахождения автомобиля в j-м состоянии.

Вероятности состояний автомобиля Р₀, Р₁, Р₂ … Р_j … P_n как функции пробега в случае марковского процесса с дискретными состояниями и непрерывным временем удовлетворяют определенного вида дифференциальным уравнениям (ДУ) – уравнением Колмогорова, следующего вида:

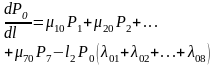
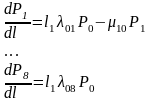
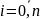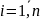где, Р_i – вероятность нахождения автомобиля в i-м состоянии, ; λ_0i – интенсивность перехода автомобиля из нулевого в i-е состояние, ; μ_i0 – интенсивность перехода автомобиля из i-го в нулевое состояние, 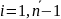; 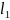– коэффициент, отражающий связь между наработками в днях и километрах пробега (среднесуточный пробег, тыс. км).

Число уравнений в системе зависит от числа состояний автомобиля.

Для описания процесса функционирования группы автомобилей может быть использован метод динамики средних. Этот метод вытекает из теории марковских случайных процессов. Удобство его заключается в том, что зная возможные состояния одного (условного) автомобиля, можно моделировать процесс функционирования группы из любого числа автомобилей.

При этом каждое состояние характеризуется средней численностью автомобилей N_j(t), находящихся в нем в момент времени t. Очевидно, что для любого t сумма численностей всех состояний равна общей численности автомобилей исследуемой группы: N= .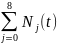

Величина N_j(t) для любого t представляет собой случайную величину, а при меняющемся t – случайную функцию времени.

Зная граф состояний и соответствующие интенсивности перехода λ_ij и μ_ij, определим средние численности автомобилей N₀, N₁, N₂ … N₈ как функции пробега l.

Согласно графу состояний система ДУ для средних численностей состояний запишется следующим образом:

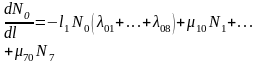
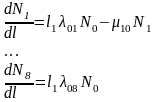
Отношение N₀/N равно коэффициенту выпуска автомобилей определенной модели на пробеге l с начала их эксплуатации.

Для расчета средней численности автомобилей, находящихся в исправном состоянии, можно предварительно объединить состояния S₁, S₅, S₆ в одно состояние: «исправен» - S₁`. Тогда граф состояний условного автомобиля примет вид:

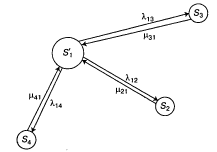
Система ДУ для средних численностей подвижного состава запишется следующим образом:

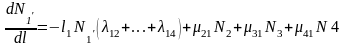
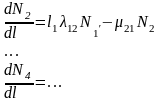
Положим левые части уравнений равными нулю, получим систему алгебраических уравнений для средних численностей состояний автопарка, работающего в стационарном режиме: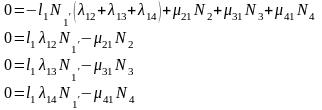

Решим систему алгебраических уравнений с учетом так называемого нормировочного условия: N₀=N₁+N₂+N₃+N₄, где N₀ – среднесписочная численность автопарка, шт.

Из системы определим неизвестные средние численности состояний, используя 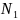. Так из второго и третьего уравнений имеем:

;

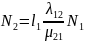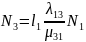
Согласно нормировочному условию: .

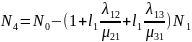Подставляя в первое уравнение, получим:

.

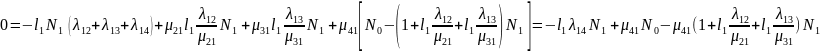Последнее уравнение можно записать следующим образом:

.
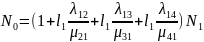