- •1. Імітаційне моделювання.
- •4. Інгредієнт економічного показника Ризик як міра мінливості результату
- •6. Канонічна форма матриці ланцюга Маркова.
- •2. Генерування випадкових величин.
- •7. Фундаментальна матриця Ланцюга Маркова.
- •3. Аналітичний ієрархічний процес. Рейтинг. Коефіцієнт погодженості
- •5. Семіваріація та семіквадратичне відхилення
- •8. Класифікація ланцюгів Маркова.
- •15. Непрямий метод найменших квадратів оцінювання точно ідентифікованих систем.
- •16. Системи одночасних рівнянь. Структурна та зведена форми системи рівнянь.
- •9. Неперервні ланцюги Маркова. Рівняння Колмогорова.
- •10. Процеси розмноження та вимирання.
- •13. Метод скользящего среднего. Простое скользящее среднее. Сао.
- •14. Взвешенное скользящее среднее. Экспоненциальное сглаживание.
- •11. Моделювання роботи автопідприємства за допомогою ланцюгів Маркова.
- •17. Необхідні й достатні умови ідентифікованості. Перша і друга умова ідентифікованості.
- •12. Приклад розрахунку роботи автопідприємства за допомогою ланцюгів Маркова
- •Імітаційне моделювання.
1. Імітаційне моделювання.
Цель имитационного моделирования – создать среду, устройство, позволяющее путём эксперимента получить нужную информацию об объектах окружающего мира, непосредственно не общаясь с этими объектами. При проведении количественного анализа имитация является основой экспериментов, проводимых на математических моделях. Хотя и при имитации, и при оптимизации используются количественные модели, эти модели строятся исходя из разных концепций. Основное различие этих моделей заключается в той роли, которую в них играют переменные решения. В задачах оптимизации значение переменных решения является выходом модели. А выходным результатом процесса оптимизации будут переменные решения, которые оптимизируют целевую функцию.
В имитационных моделях значения переменных являются входом модели. Выходным результатом в процессах имитации будет значение целевой функции
оптимиз:
min(max):
Q( )
) 0
- установить
0
- установить
имитац:
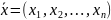 <-уже задан , z(
)
<- установить
<-уже задан , z(
)
<- установить
4. Інгредієнт економічного показника Ризик як міра мінливості результату
Вважають, що економічний показник Х має позитивний інгредієнт, якщо при прийнятті рішення орієнтуються на його максимальне значення. В цих випадках пишуть, що Х=Х+. Якщо при прийнятті рішення орієнтуються на його мінімальне значення, то вважають, що він має негативний інгредієнт. І в цьому випадку пишуть Х=Х-.
В якості величини ризику можуть виступати математичне сподівання, дисперсія, середнє квадратичне відхилення. Підхід до оцінки ризику, що спирається на дисперсію, вважається класичним. Причому, чим більшими будуть ці величини, тим більше буде ступінь ризику.
6. Канонічна форма матриці ланцюга Маркова.
Ланцюг Маркова називають поглинальним, якщо серед множини станів відповідної системи існує хоча б один, набувши якого з певною імовірністю система перебуватиме в ньому й надалі. Отже, поглинальними є такі ланцюги Маркова, для яких стійкими станами є поглинальні.
Розглядаючи поглинальні ланцюги Маркова, стани процесу нумерують так, щоб поглинальні дістали перші номери, тоді ця матриця називається канонічною формою матриці.
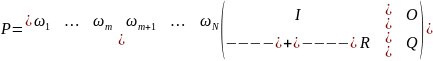
I – одинична матриця розміру m*m
O – матриця m* (N-m), усі елементи якої =0.
Q – матриця розміру (N-m) * (N-m), елементами якої є імовірності переходів системи з непоглинальних станів до непоглинальних.
R – (N-m)*m, елементами якої є імовірності, що визначає перехід системи з непоглинального стану до поглинального.
Приклад.
За
даною матрицею ймовірностей однокрокового
переходу поглинального ланцюга
Маркова
![]() побудувати
її канонічну форму.
Розв’язання.
Матриця
π описує поглинальний ланцюг Маркова
з чотирма станами ω1,
ω2,
ω3,
ω4,
із яких стан ω4 є
поглинальним.
Тому для матриці
побудувати
її канонічну форму.
Розв’язання.
Матриця
π описує поглинальний ланцюг Маркова
з чотирма станами ω1,
ω2,
ω3,
ω4,
із яких стан ω4 є
поглинальним.
Тому для матриці
![]() канонічна
форма набирає такого вигляду:
канонічна
форма набирає такого вигляду:
![]() ,
де
I=(1);
O
= (0 0 0);
,
де
I=(1);
O
= (0 0 0);