3. Задача о «расшивке узких мест производства»

При выполнении оптимальной производственной программ второй и третий ресурсы используются полностью, то есть образуют “узкие места производства”. Будем заказывать их дополнительно. T = (t₁, t₂, t₃) – вектор дополнительных объёмов ресурсов.

Итак, необходимо составить план “расшивки узких мест“ производства, то есть указать, сколько единиц каждого из дефицитных видов ресурсов должно быть приобретено, чтобы суммарный прирост прибыли был максимальным при условии, что для расчетов используются найденные двойственные оценки ресурсов.

Так как мы используем найденные оценки ресурсов, то должно выполняться условие:

H + Q^-1T ³ 0

Задача состоит в том, чтобы найти вектор Т(t₁;0;t₂), максимизирующий суммарный прирост прибыли W = 7t₁ + 5t₃ при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы).

Обращённый базис Q, соответствующий оптимальной производственной программе, содержатся в последней симплексной таблице в первой, второй, третьей строках восьмого, девятого и десятого столбцов:

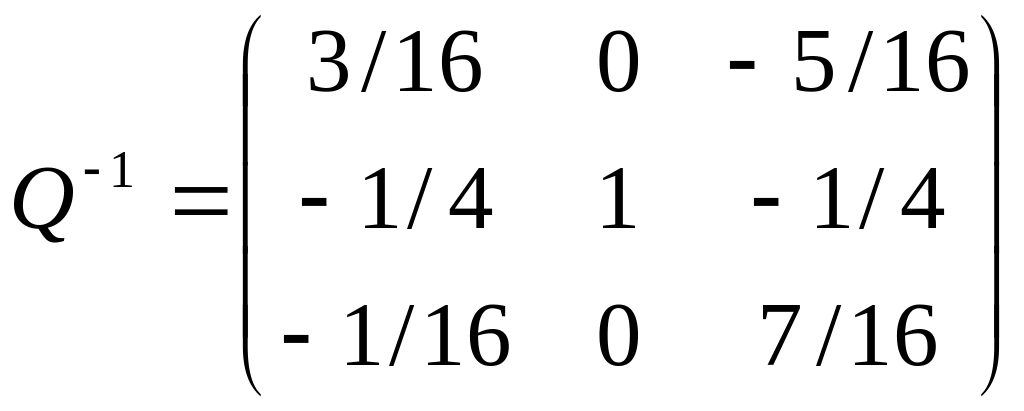
Подставив соответствующие значения, получим требуемую математическую модель:

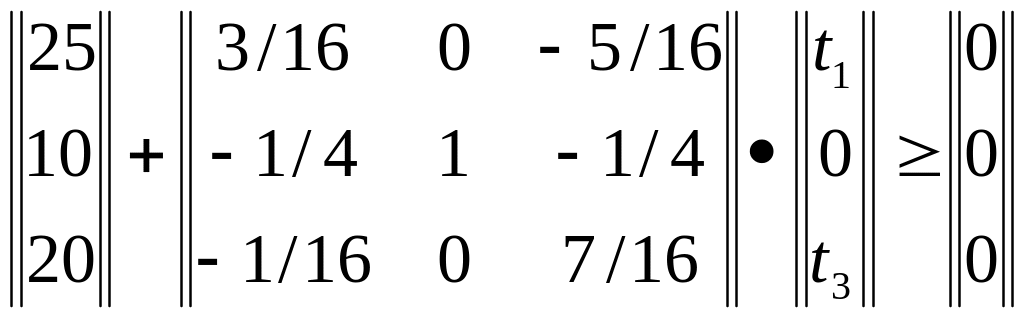
предполагая, что дополнительно можно надеяться получить не более 1/3 первоначального объёма ресурса каждого вида, то есть

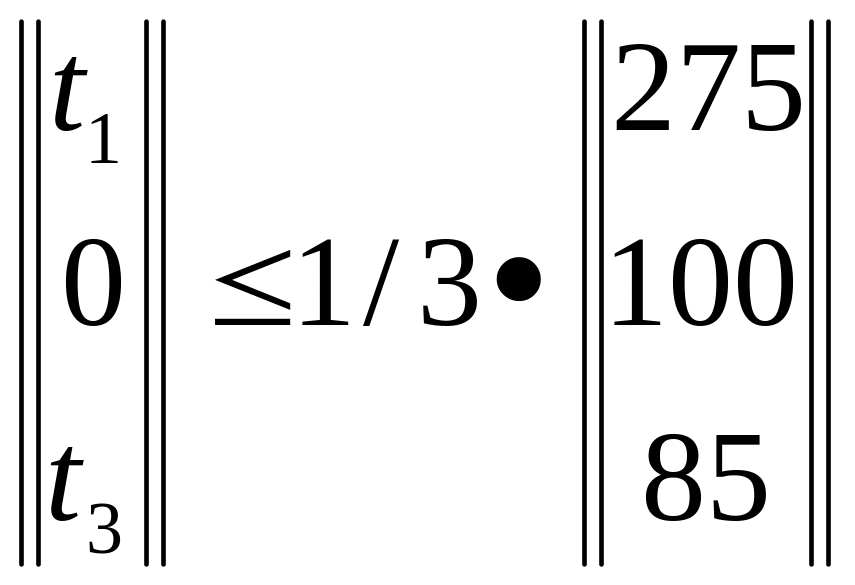
причём по смыслу задачи t₂ ³ 0, t₃ ³ 0. Перепишем неравенства в другом виде. Получим:

W = 7t₁ + 5t₃  max

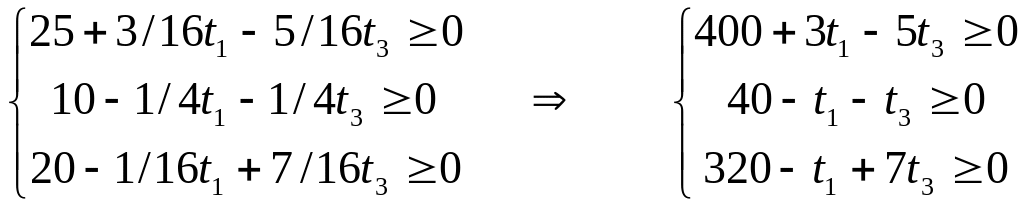
t₁  275/3, t₃  85/3 t₁  275/3, t₃  85/3

По графику видно, что решение данной задачи находится в точке А(11,3;28,3). Таким образом, программа «Расшивки узких мест производства» имеет вид: t₁=11,3, t₂=0, t₃=28,3 и прирост прибыли составит W = 7*11,3 + 5*28,3 = 220,6

Сводная таблица результатов:

Cj	50	27	34	54	Bi	X4+i	Yi	Ti
	5	4	6	7	275	0	7	11,3
aij	2	0	4	2	100	10	0	0
	3	2	0	1	85	0	5	28,3
Xj	20	0	0	25	2350			220,6
j	0	11	8	0

4. Транспортная задача линейного программирования

Имеется 3 производителя однородной продукции, имеющие запасы этой продукции 70, 50 и 54 единицы соответственно. Также имеется 4 потребителя данной продукции. Их потребность составляет 50, 27, 34 и 54 единицы соответственно. Транспортная компания заключила контракт с поставщиками и потребителями на вывоз и поставку данной продукции от производителей к потребителям. При перевозке продукции от каждого производителя к каждому потребителю транспортная компания имеет определённые издержки на единицу продукции: 5 у.е. при перевозке от 1-ого производителя к 1-ому потребителю, 4 у.е. - от 1–ого производителя ко 2-ому потребителю, 6 у.е. – от 1-ого к 3-ему, 7 у.е. – от 1-ого к 4-ому, 7 у.е. – от 2-ого к 1-ому, 3 у.е. – от 2-ого ко 2-ому, 4 у.е. – от 2-ого к 3-ему, 2 у.е. – от 2-ого к 4-ому, 3 у.е. – от 3-его к 1-ому, 2 у.е. – от 3-его ко 2-ому, 5 у.е. – от 3-его к 3-ему, 1 у.е. – от 3-его к 4-ому. Так как естественным стремлением транспортной компании является максимизация прибыли, то требуется составить такой план перевозок, чтобы издержки были минимальными.

Можно записать эти издержки на единицу продукции в виде матрицы, где строка издержки при поставке от одного производителя к каждому потребителю, а столбец издержки при поставке к одному потребителю от каждого производителя:

Предложение производителей и спрос потребителей можно записать в виде векторов А и B соответственно:

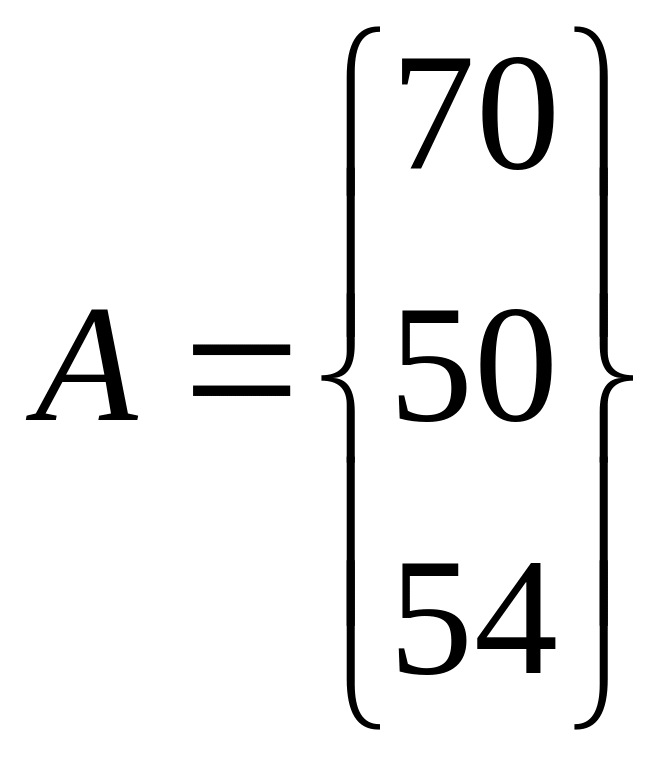и

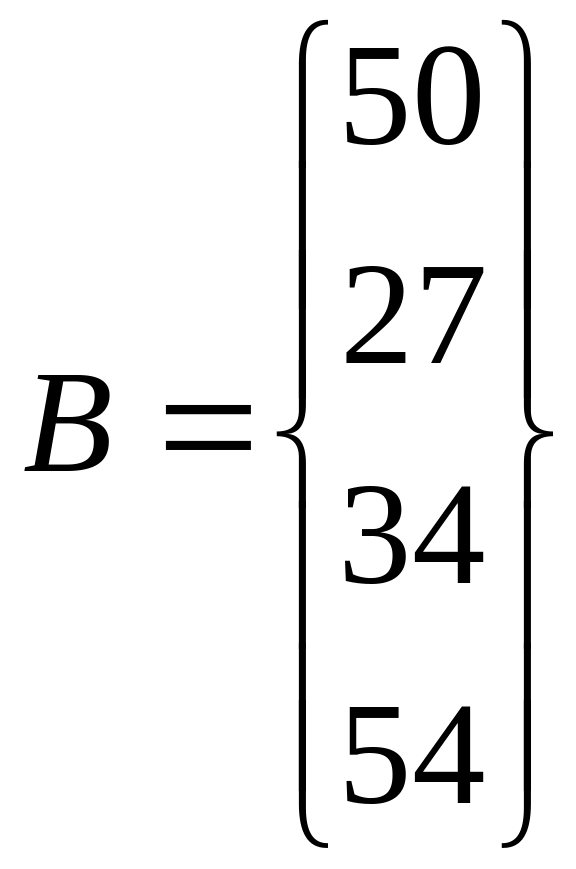
Требуется найти план перевозок

X = (x_ij), i = 1,m; j = 1,n,

минимизирующий общую стоимость всех перевозок

L = c_ijx_ij

При условии, что из любого пункта производства вывозится весь продукт

x_ij = a_i, i = 1,m

И любому потребителю доставляется необходимое количество груза

x_ij = b_j, j = 1,n

Причём по смыслу задачи

x₁₁ > 0,…, x_mn > 0

В нашей задаче 4 потребителя и 3 поставщика, причём суммарный объем производства a_i = 70 + 50 + 54 = 174 больше, чем требуется всем потребителям b_i = 50 + 27 + 34 + 54 = 165. Суммарное предложение не больше суммарного спроса. Для того, чтобы они были равны введём фиктивного потребителя с потреблением равным разнице между предложением и спросом.. Фактически эта потребность будет указывать на количество продукции, которая не будет вывозиться от производителя. Для того, чтобы введение фиктивного потребителя не повлияло на решение, затраты на перевозку единицы продукции к фиктивному потребителю приравняем к 0. В действительности это будет также, так как транспортная компания не будет нести издержки за товар, который она никуда не возит. Тогда вектор В и матрица С будут выглядеть так:

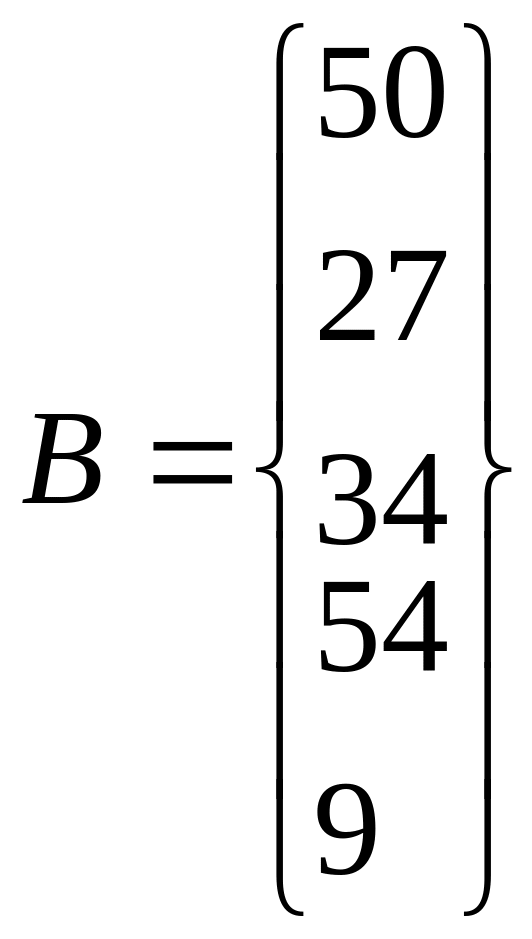и

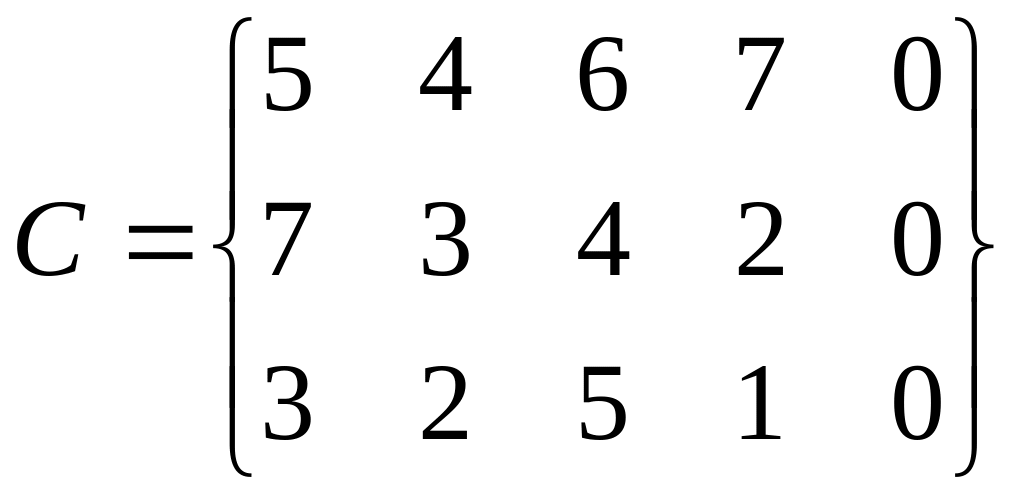
50 + 27 + 34 + 54 + 9 = 70 + 50 + 54

ПН ПО	50		27		34		54		9		αi
70	5	5	4	4	5	6	3	7	2	0	α1 = 0
	50		2 0
	0		0		-1		-4		2
50	4	7	3	3	4	4	2	2	1	0	α2 = -1
			7		34		9
	-3		0		0		0		1
54	3	3	2	2	3	5	1	1	0	0	α3 = -2
							4 5		9
	0		0		-2		0		0
βj	β1 = 5		β2 = 4		β3 = 5		β4 = 3		β5 = 2

Z_опор = 250 + 80 + 21 + 136 + 18 + 45 = 550

Для заполненных клеток α _i + β _j = C_ij, для них _ij = 0

Для незаполненных клеток _ij= α _i + β _j - c_ij

Так как не все характеристики отрицательны (например, ₁₅ = 2), то для найденной свободной клетки строим цикл пересчёта. Производим перераспределение поставок вдоль цикла пересчета:

ПН ПО	50		27		34		54		9		αi
70	5	5	4	4	5	6	3	7	0	0	α1 = 0
	50		11						9
	0		0		-1		-4		0
50	4	7	3	3	4	4	2	2	-1	0	α2 = -1
			16		34		0
	-3		0		0		0		-1
54	3	3	2	2	3	5	1	1	0	0	α3 = -2
							54
	0		0		-2		0		0
βi	β1 = 5		β2 = 4		β3 = 5		β4 = 3		β5 = 0

Решение оптимально, так как все   0.

Ответ: 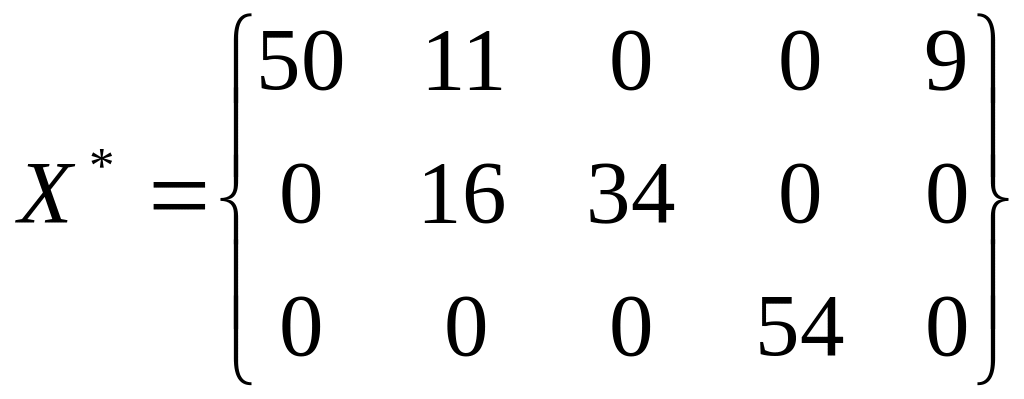При этом 9 единиц продукции остаются у 1-ого производителя.

Z_опт = 250 + 44 + 48 + 136 + 54 = 532

Z = Z_опор – Z_опт = 550 – 532 = 18