Сопряженные операторы

Пусть существует банаховы X,Y и линейный непрерывный оператор A:XY и рассмотримx^*,y^*

можно определить сопряженный оператор к A, A^*:Y^*X^*

и действует следующим образом : y^*Y^* (A^*y^*,x)=(y^*,Ax).

Утв:||A^*||_Y^*_X^*=||A||_XY

Утв:ПустьX – банахово, тогда(I_x)^*=I_x*

Утв:(BA)^*=A^*B^*

ТеоремаПусть существует банаховыX,Y иA:XYдля того, чтобы операторA был обратим необходимо и достаточно, чтобыA^*, былобратим и выполнялось (A^-1)^*=(A^*)^-1

Понятие сепарабельности и несепарабельности

Опр:Пусть существует банахово пространствоX и Пусть существует некое подмножествоEX, будем говорить, что множествоE всюду плостно вX, если>0 иxX существуетaE : ||a-x||<

Опр:Пусть существует банаховоX оно называется сепарабельным, если существует его счетное всюду плотное подмножество, т.е. существует, a_nX : >0 иxX существует n₀ : ||a_n0-x||<, если же дляXневозможно найти счетного всюду плотного подмножества, оно называется несепарабельным.

Мепарабельными являются следующие подмножества l

1. l^p, 1<p<

2. L^p(E), 1<p<

3. С(K)

Несепарабельными:

1. l^

Предгильбертовы пространства

Опр:: Пусть есть линейное пространство (R или С)L. Это пространство будем называтьПредгильбертовым, если определены операции скалярного произведения:

Для xL иyL:

(x,y) R (илиC)

и эти операции обладают следующими свойствами:

Вещественные	Комплексные
(x,x)0	(x,x)0
(x,x)=0 <=> x = 	(x,x)=0 <=> x = 
(x1+x2,y) = (x1,y)+(x2,y) (x,y1+y2) = (x,y1)+(x,y2)	(x1+x2,y) = (x1,y)+(x2,y) (x,y1+y2) = (x,y1)+(x,y2)
(ax,y)=a(x,y) aR (x,ay)=a(x,y) aR	(ax,y)=a(x,y) aC (x,ay)=(x,y)aC
(y,x)=(x,y)	(y,x)=

Норма в Гильбертовом пространстве

Утв ПустьL– вещественное или комплексное гильбертово пространство, тогда нормаx:

||x|| =

Лемма: Справедливо |(X,y)|||X||*||y||

Опр:: Пусть есть предгильберово пространство вещественное или комплексное. Если оно является полным относительно нормы, то оно называетсягильбертовым пространством.

Ортогональное разложение гильбертова пространства.

Опр:: Пусть H – гильбертово пространство, x,yH – называются ортогональными, если (x,y) = 0.

УтвПустьH₁ H, H₁  {}, H₁  H.

Тогда существует y₀H₁, y₀H₁, такое что:

(y₀,x) = 0 xH₁.

Опр:: множество всехy₀{ }H, удовлетворяющих приведенному выше условию, будем обозначатьH₁^.

УтвЛинейное пространствоH₁^ оказывается полным относительно нормы, введенной с помощью скалярного произведения, употребляемой на всем пространстве. Это линейное пространство называется ортогональным дополнением подпространства H₁ и само является подпространством.

Ортогональные ряды в гильбертовом пространстве

Опр:: Рассмотрим рядx_n , гдеx₁, x₂,… x_n… H.

Этот ряд называется ортогональным рядом, если n,m: n#m справедливо:

(x_n,x_m) = 0.

ТеоремаПусть имеется ортогональный ряд, тогда его элементы линейно независимы.

Лемма: Пусть есть гильбертово пространствоHиx₁, x₂,… x_n… H, причем x_k#0 k и (x_k,x_l) = 0 ( дляk,l: k # l).

Тогда они ЛНЗ.

Опр:: Гильбертово пространствоHбудем называть конечномерным, если: N: любые x₁, x₂,… x_N, гдеx_j # 0 дляj – линейно независимы.

Опр:: Пусть естьH₁,H₂ – гильбертовы пространства. Будем называть их изометричными, если:

• они изометрично изоморфны как банаховы пространства.

• A: H₁H₂ иx,yH₁ выполняется:

(Ax,Ay)_H2 = (x,y)_H1.

ТеоремаВсякое конечномерное Гильбертово пространство, изометричное пространствуRⁿ, изометрично пространствуCⁿ.

Опр:: Гильбертово пространство, которое не является конечномерным, называется бесконечномерным.

Опр:: Пусть естьH– бесконечномерное Гильбертово пространство, тогда для любогоnx₁, x₂,… x_n, (где x_k#0 k)

1. ||x_k|| = 1 (k)

2. (x_k,x_l) = 0 ( дляk,l: k # l).

V_n - множествоx₁, x₂,… x_n. Будем называть V_n – конечной ортонормированной системой.

А a_k = (по опред) = (y,x_k) – этоk-й коэффициент ряда Фурье.

Неравенство Бесселя.

Пусть V_{n -} конечная ортонормированная система из элементов x₁, x₂,… x_n, a_k -k-й коэффициент ряда Фурье, тогда:

|a₁|² + |a₂|² +…+ |a_n|²  ||y||².

Опр::Пусть естьH-гильбертово пространство и естьEH. Будем говорить, что мрожество полно в гильбертовом пространчтве, если из условия (x,a) = 0 (дляaE) следуетx = 0.

УтвПустьE– всюдуплотное множество вH, тогдаE– плотно вH.

Следствие:ЕслиH– сепарабельное Гильбертово пространство, то в нем существует счетное плотное множество.

ТеоремаВо всяком сепарабельном Гильбертовом пространстве существует конечная или счетная полная ортонормированная система. При этом она оказывается конечной, если пространство конечно, и оказывается бесконечной, если пространство бесконечное.

Опр:: ПустьL – пространствоx₁, x₂,… x_mL. Линейной оболочкойZ(x₁, x₂,… x_m) этих элементов будем называть множество комбинаций:

{c₁x₁+c₂x₂+ … +c_mx_m R (илиC)}.

Лемма: Если мы рассмотрим линейную оболочку любого конечного числа элементов в пространстве H, то эта линейная оболочка является поным подмножеством вH.

Теорема замкнутости: (Равенство Парсеваля):

Пусть есть H– Гильбертово пространство (сепарабельное, бесконечномерное) иl₁,l₂,…l_n… - полная ортонормированная система, тогда:

a_n = (x,l_n) ,  xH

b_n = (y,l_n) ,  yH

и выполняется:

1)

при этом:

3. 

Опр:: Пусть есть H- Гильбертово пространство ( сепарабельное и бесконечномерное). Система f_nH. Для xH  a_n (и единственное) (a_nC):

Такая система называется базисом в H.

Вывод: Итак, нами доказано, что полная ортогональная система в любом сепарабельном бесконечномерном пространстве существует и является базисом в этом пространстве.

Структурная теорема о сепарабельном бесконечномерном простанстве:Всякое вещественное сепарабельное бесконечномерное Гильбертово пространствоHизометричноl_R², а всякое комплексное сепарабельное бесконечномерное Гильбертово пространство изометричноl_C².

Каноничная инволюция в H.

Пусть есть H(сепарабельное б/мерное Гильбертово пространство) и {l_n}– его ортонормированная система. Тогда xH:

УтвКаноническая инволюцияJx– не зависит от выбора{l_n}.

Свойства Jx: 1)J(x+y) = Jx+Jy.

2)  cC: J(cx) = Jx

Описание сопряженного комплексному бесконечномерному сепарабельному Гильбертову пространству.

H – Гильбертово пространство. РассмотримH*: Пустьy*H*, xH, тогда

(y*,x) – линейный функционалy*, действующий наx.

Пусть {l_n}^_n=1 – полная ортонормированная система.

(y*,x) = (y*,a_nl_n) = (y*,a_nl_n) = a_n(y*,l_n)

Опр::Положим_n = (y*,l_n).

Лемма: Пусть_n = (y*,l_n), тогда справедливо:

Элементы спектральной теории операторов.

Пусть H– комплексное Гильбертово пространство, и есть линейный ограниченный оператор T: HH.

TT = T²: HH

TT…T = Tⁿ: HH.

P(z) = a₀+a₁z+…+a_nzⁿ.

A = P(T) = a₀I+a₁T+…a_nTⁿ.

Рассмотрим другой полином: q(z) и q(T).

Когда P(T) = q(T) приPq?

Пусть есть T: HH. Существует ли B: HH, такой чтоT = B²?

Рассмотим конечномерное Гильбертово пространство Cⁿ:

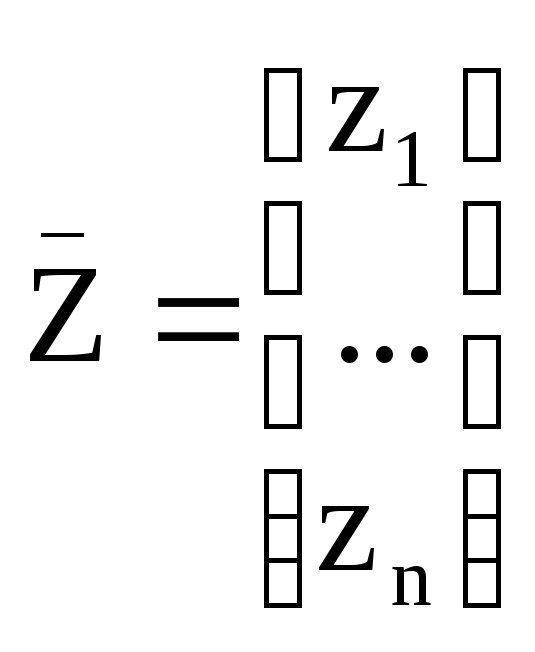
и есть T: Cⁿ Cⁿ, ему можно сопоставить матрицу:

TZ =

T²  ² и понятно, чтоT^K  ^K

Пусть есть два многочлена p иq, p # q. Введемr = p-q.Еслиp # q, то r # 0. Если же p = q (как операторы), тоr = 0. (1)

С матрицей Tможно связать характеристический многочлен():

Теорема Кэли:Для того, чтобы выполнялось (1) необходимо и достаточно, чтобы существовал многочленk(): r() = () k() (2)

Где () – характеристический многочлен для матрицы T,r() - характеристический многочлен для разности, т.е, если (1)<=>(2), то

(T) = 0, r(T) = 0.

То есть вопрос в делимости r() на ().

Опр::Комплексное число будем называть регулярной точкой оператора T, если оператор^-1I-Tимеет обратный оператор.

Опр:: Если - регулярная точка оператора T, тогда резольвентой оператораTв точке будем называть обратный операторR(^-1,T) = (^-1I-T)^-1. При этом выполняется:(^-1I-T) R(^-1,T) = R(^-1,T) (^-1I-T) = I.

Опр::Множеством всех регулярных точек называется регулярным или резольвентным множеством. Обозначается(T).

Утв ЕслиH– конечномерно и₁,… _n– различные собственные числа оператораT, то(T) = С\ .

Опр:: Спектром оператора T(T) – называется:(T) = С\(T) – множество всех резольвентых точек:

(T) =

Принципиальная теорема о спектре оператора и его резольвенте:Резольвентное множество оператора непусто и открыто. Спектр оператора замкнут и непуст.

Лемма: Оператор R_N = ^-1I + - образует фундаментальную последовательность в банаховом пространстве.

Вполне непрерывные компактные операторы.

Опр::Пусть имеетсяT: HH, где H– бесконечномерное сепарабельное Гильбертово пространство. Будет называтьT– компактом, если:

x_nH: ||x_n||  M (n)

из последовательности Tx_nможно выбрать сходящуюся подпоследовательность.

ТеоремаСпектр компактного оператора не имеет С точек сгущения, кроме возможно, точки 0.

Опр::Ненулевой элемент x_j, удовлетворяющий соотношениюTx_j = x_j, называется собственным элементом оператораT.

Операторы, сопряженные по Гильберту.

Опр::Гильбертовым сопряженным к А мы будем называть такой оператор А_*: А_*: НН, такой чтоx,yH:

(Ax,y) = (x,A_*y).

ТеоремаГильбертов сопряженный оператор к линейному оператору А существует, единственен и является линейным оператором А_*: НН.

Теорема||А_*|| = ||A||.

Существенное свойство:(A_*)_* = A.

Опр::ОператорA: HH– самосопряженный, если А_*= А. Тогда справедливо:(Ax,y) = (x,Ay).

Важное наблюдение:Пусть А – самосопряженный оператор в Гильбертовом пространстве, тогда:

(Ax,y) = (x,Ay) = .

Теорема Пусть А – самосопряженный оператор в Гильбертовом пространстве, тогда спектр оператора А – вещественный и принадлежит области[-||A||, ||A||].

Положительно определенные операторы.

Опр::Пусть А – самосопряженный оператор в Гильбертовом пространстве. А – положительно определенный оператор, еслиm>0, не зависящее отx, такое, что:

(Ax,x)  m||x||², xH.

Уточнение из предыдущей теоремы:Если А – положительно определенный оператор, то(A) [m, ||A||], гдеm – см. выше.

Непрерывные банаховозначные функции и интегралы от них.

Опр::Пусть Г – непрерывная кривая, ГС, и В – Банахово пространство. Будем говорить, что у нее на Г определена банаховозначная функция отt – F(t), если:

1. tГ => F(t)B.

2. t₀Г|| F(t) – F(t₀)||_{B t0}  0.

Суммой Римана для F(t) будем называтьS_n = .

УтвЭлементыI_nобразуют фундаментальную последовательность в В, еслиmax _k| t_k – t_k-1|_n0.

Опр::= по определению =I, которое взято см. выше.

Две важные функции от ограниченных операторов.

ТеоремаОператорT_n = - образует фундаментальную последовательность в банаховом пространстве, т.е.||T – T_n|| _n0.

Утвe^A=T - по определению и справедливо || T ||  e^||A||.

Корень квадратный из положительно определенного оператора.

Пусть А: НН - положительно определенный оператор, тогда (Ax,x) m||x||².

Рассмотрим Г – эллипс, лежащий строго в правой полуплоскости и содержащий m и||A||. Для всякогоГ существует резольвентаR(,A)Y и R(,A)Y.

Пусть В = - некоторый интеграл вY.

УтвВ – является линейным непрерывным оператором: НН и В²= А.