
- •Эквивалентность функций
- •Интеграл Лебега
- •Обобщенные Функции (Лоран Шварц)
- •Полунормы в комплексном пространстве Опр: Пусть существует линейное l (может состоять только из нуля)
- •Линейные функционалы на счетнолинейном пространстве
- •Опр:линейных непрерывных функционалов на счетнонормированном пространстве
- •Пример обобщенных функций
- •Абсолютная непрерывность интегралов Лебега от суммируемых функций
- •Носитель (спектр) обобщенной функции
- •Действия которые можно производить над обобщенными функциями
- •Метрические пространства
- •Важное Опр:
- •Банаховы пространства
- •Сопряженное пространство
- •Принципиальное Опр:
- •Неравенство Гельдера
- •Сопряженные операторы
- •Понятие сепарабельности и несепарабельности
- •Предгильбертовы пространства
- •Лемма: Справедливо |(X,y)|||X||*||y||
- •Ортогональное разложение гильбертова пространства.
- •Ортогональные ряды в гильбертовом пространстве
![]() Функциональный
анализ.
Функциональный
анализ.
Опр:Рассмотрим Rnпространств (n>=1).
Пусть существует
набор чисел![]()
Открытым
параллелепипедом P будет множество
точек с координатами![]() Замкнутый параллелепипед
Замкнутый параллелепипед![]()
Полуоткрытый
параллелепипед
![]()
n=1 промежуток
n=2 прямоугольник
По определению объема параллелепипеда V(P)=V(P)=V(Q)=(b1-a1) (b2-a2)…(bn-an)
n=1 длина промежутка
n=2 площадь прямоугольника
Множество E, ERnмы будем называть основным, если существует S1, … Sm, .. где любое Skявляется либо P, либоP, либо Q
![]() (объединение
может быть счетное)
(объединение
может быть счетное)
Утв:Любое
основное множество может быть представлено
в виде конечного или счетного объединения:![]() :kl=,
kl
:kl=,
kl
Опр:Пусть основное множество представлено
в виде параллелепипедов![]() :kl=,
kl, тогда по определению
объемом основного множества называется
V(E)=
:kl=,
kl, тогда по определению
объемом основного множества называется
V(E)=![]() ,
если этот ряд сходится. Если этот ряд
расходится, то V(E)=+
,
если этот ряд сходится. Если этот ряд
расходится, то V(E)=+
ТеоремаПринципиальная теорема о корректности определения объема основной фигуры.
Пусть существует
основное множество в Rn, ERn,
представленное в виде объединения
других не пересекающихся параллелепипедов.![]() и
и![]() ,
гдеиkпопарно
не пересекаются =>
,
гдеиkпопарно
не пересекаются =>
![]() =
=![]() ,
если сходится один из них и суммы равны,
то второй сходится, либо оба расходятся,
т.е. объем основной фигуры не зависит
от разбиения.
,
если сходится один из них и суммы равны,
то второй сходится, либо оба расходятся,
т.е. объем основной фигуры не зависит
от разбиения.
Опр:Пусть существует множество SRn, оно будет называться дополнительным, если существует некий параллелепипед P любого типа, и если существует основное множество EP : S=P\E
Опр:Объемом дополнительного множества называется V(S)=V(P)-V(E)
ТеоремаПринципиальная теорема о корректности определения объема дополнительного множества. Пусть существует S=P\E=P1\E1, где P, P1– произвольные параллелепипеды, E, E1– основные множества
V(P)-V(E)=V(P1)-V(E1)
ТеоремаОб универсальности термина объема.
Пусть существует множество Т которое является и основным и дополнительным. Пусть Vосн(T) – объем от Т как основное множество, Vдоп(T) – объем Т как дополнительно множество, тогда эти величины совпадают Vосн(T)=Vдоп(T)
Принципиальные примеры оновных, дополнительных множеств.
Любое открытое и не пустое множество в Rnявляется основным множеством.
Любой компакт является дополнительным множеством.
Опр:Понятие внешней меры множества.
Пусть ERnограниченное => существует PE (P – параллелепипед)
Значит существует основное множество L : LE
Мы можем определить внешнюю меру множества E.
*E=![]()
Важнейшие свойства внешней меры.
*E>0
Пусть E1E2, E1,E2– ограничены =>*E1<*E2
Если
 *E<
*E<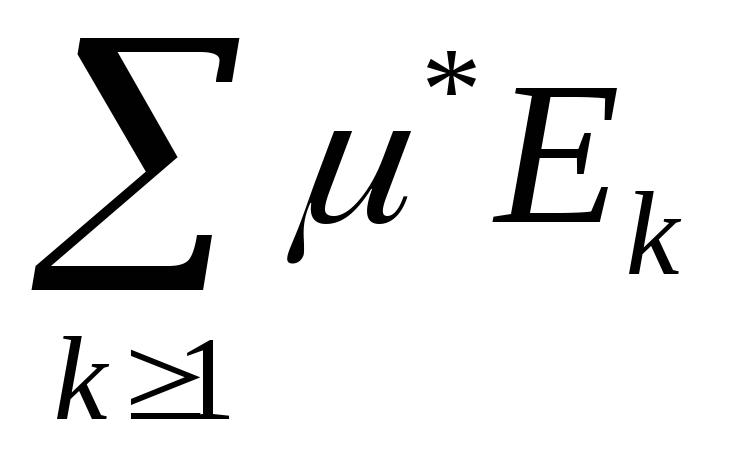 - Ek– могут попарно пересекаться
- Ek– могут попарно пересекаться
Внешняя мера определена для любого ограниченного пространства
Опр:Понятие внутренней меры
Терминологическое дополнение
Пустое множество и Rnявляется основным и дополнительным
По определению V()=0, V(Rn)=+
Пусть существует множество F – ограниченное, тогда существует K – дополнительное множество KF (например K=)
Можно рассматривать V(K) – объем дополнительных множеств.
![]() - внутренняя мера F
- внутренняя мера F
Внутренняя мера может быть определена для любого ограниченного(конечного) множества.
Принципиальные свойства внутренней меры.
*F>0
Пусть F1F2, F1,F2– ограничены =>*F1<*F2
Если F – огр.
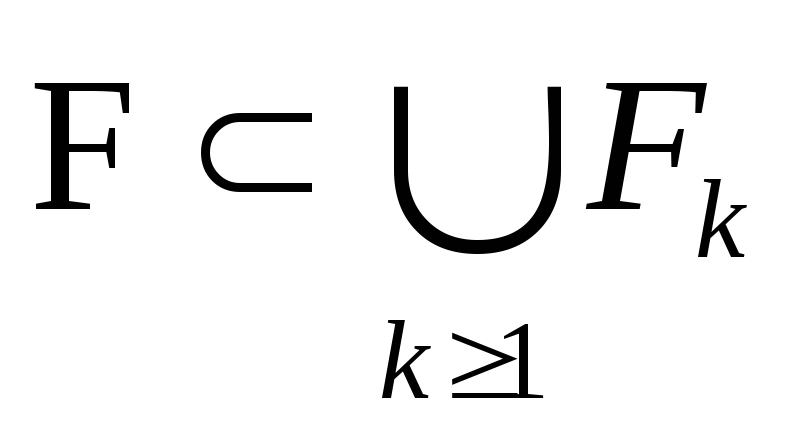 *F>
*F>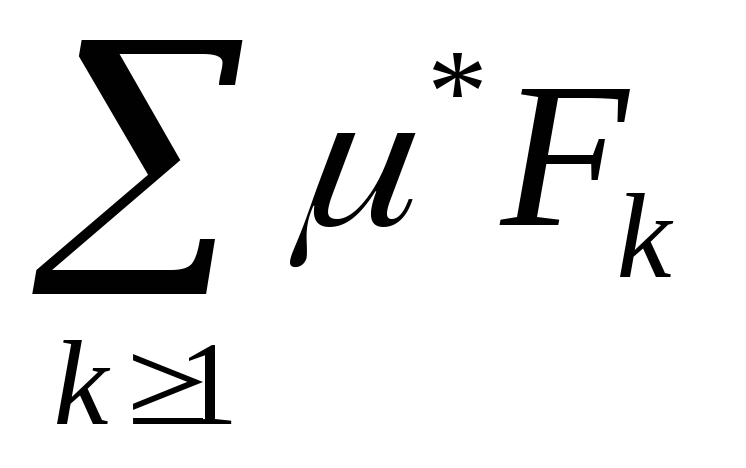 - Fk– не могут попарно пересекаться
- Fk– не могут попарно пересекаться
Для любого множества могут быть определены две характеристики: внешняя и внутренняя мера
4) E*E<*E
ТеоремаПусть Е – ограниченное множество, либо основное, либо дополнительное, тогда*E=*E=V(E) (Если нет равенства, то E очень сложное множество)
Опр:Самое принципиальноеОпр:в теории Лебега.
Пусть E – ограничено, E, ERn
Будем говорить что множество Е измеримо по Лебегу, если для него выполняется соотношение *E=*E, при этом мерой Лебега множества Е будем называть mE=*E=*E
Замечание: Из теоремы следует, что основное и дополнительное множество, если они ограничены, являются множествами измеримыми по Лебегу и мера Лебега для них равна их объему.
Счетная аддитивность меры Лебега
ТеоремаПусть множество Ek, k=1,2.. (счетное или конечное)
EkEl=, kl
![]() Ek– ограничено и измеримо по
Лебегу, тогда множество Е тоже измеримо
по Лебегу и выполняется соотношение
mE=
Ek– ограничено и измеримо по
Лебегу, тогда множество Е тоже измеримо
по Лебегу и выполняется соотношение
mE=![]()
Опр:Распространение понятия измеримости по Лебегу и меры Лебега на неограниченные множества.
Пусть ERn, E – неограниченно
Пусть BR={||x||<R} – шар с центром в 0 и радиусом К
Будем говорить, что множество E измеримо по Лебегу, если R>0, EBR– измеримо.
Основные свойства измеримых множеств:
mE>0
Пусть EF, то mE<mF
E,F – измеримы, то EF,F, E\F – измеримы
Пусть существует Ek, k>1 – конечное или счетное множества,Еk– измеримо,
 и
и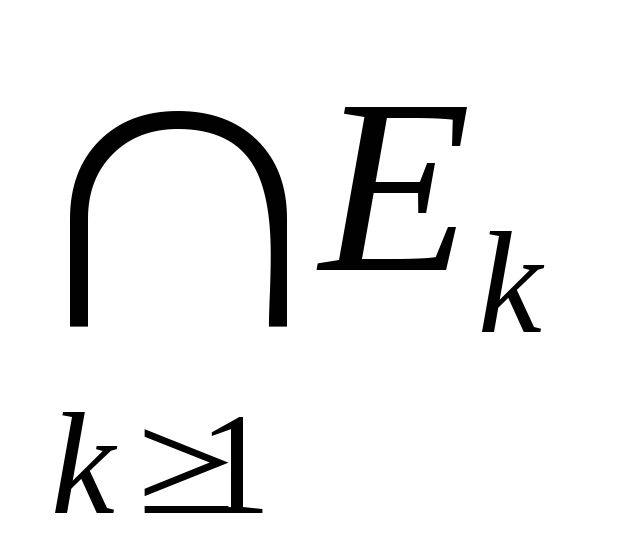 -
измеримые множества
-
измеримые множестваEkk>1 необязательно ограниченные, измеримые, попарно не пересекающиеся Пусть
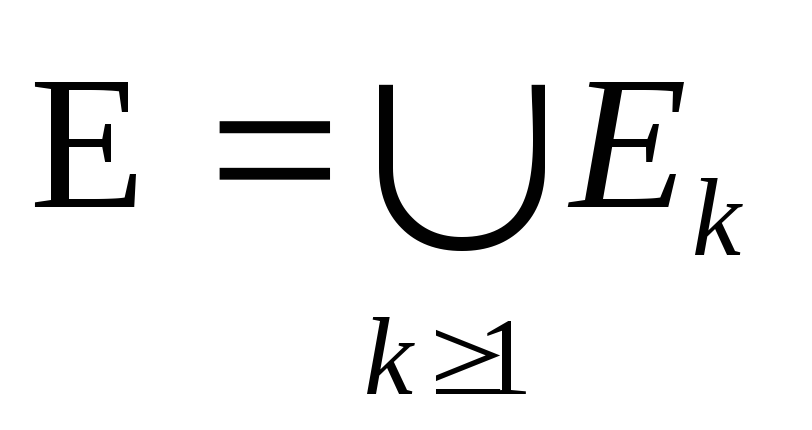 -
конечное или счетное объединение, E –
измеримо по определению и mE=
-
конечное или счетное объединение, E –
измеримо по определению и mE=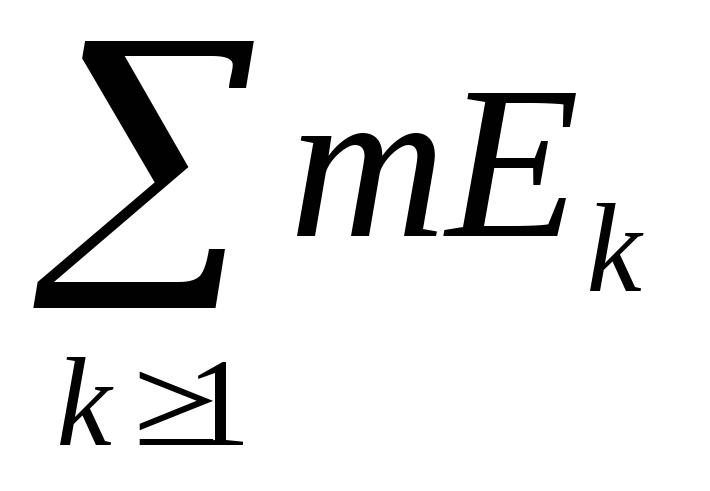 ,
если ряд сходится и mE=,
если ряд расходится
,
если ряд сходится и mE=,
если ряд расходитсяa) Пусть существует E1Е2…EkEk+1…, Ek– измеримо по Лебегу
![]() ,
тогда mE=
,
тогда mE=![]()
b) Пусть существует F1F2…FkFk+1…, Fk– измеримо по Лебегу
F=![]() ,
тогда mF=
,
тогда mF=![]()
Пусть E,Ek, k>1 – измеримые множества, Ek– счетное или конечное
![]() ,
тогда mE<
,
тогда mE<![]()
ТеоремаПринципиальная теорема о существовании измеримых множеств:
В Rnсуществует ограниченные множества E : в.с.*E<*E, такие множества называются неизмеримыми по Лебегу.
Множества меры нуль и некоторые их свойства:
Опр:Множество ERnизмеримо по Лебегу называется множеством меры нуль, если mE=0
Утв:Для того, чтобы множество E было множеством меры нуль, необходимо и достаточно, чтобы*E=0
Следствия:
Множество ERnявляется множеством меры нуль тогда и только тогда, когда>0 существует основное множество L : EL и V(L)<
Пусть ERnмеры нуль и пусть существует FE, тогда mF=0
Пусть существует EkRnEk– счетное или конечное множество k>1,Ek– меры нуль
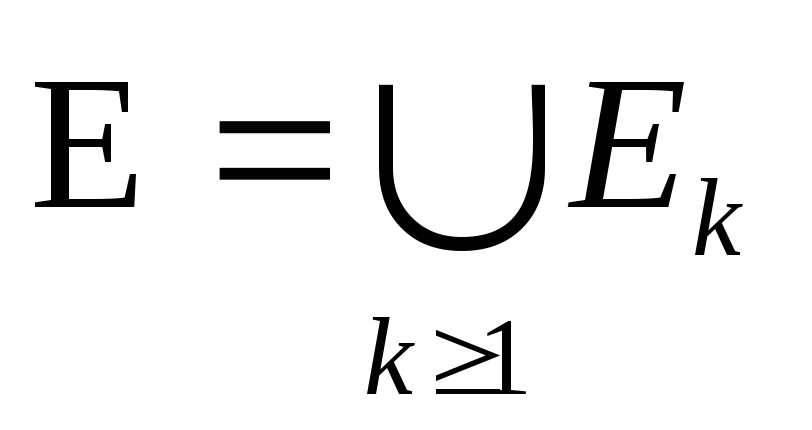 ,
тогда E – множество меры нуль.
,
тогда E – множество меры нуль.
Важный термин
В дальнейшем, если некое рассматриваемое свойство будет справедливо для (), какого-то множества, за исключением какого-то множества меры нуль, то говорят, что это свойство выполняется почти всюду.
Утв:mQ=0,
т.к.![]() rk– точки, мера точки = нуль
rk– точки, мера точки = нуль
Следствие:
Рассмотрим интервал (a,b), Пусть I=(a,b)\Q
K=(a,b)Q => KQ => mK=0
т.к. (a,b) и Q – измеримы, то I – измеримо
IK=(a,b), IK==> mI+mK=m(a,b)=b-a=> mI=b-a, т.е. иррациональных чисел, много больше, чем рациональных.
Свойства измеримых множеств при линейных преобразованиях в Rn
Пусть Е aRn(a – вектор)
Рассмотрим преобразования ha:xRnx +a (параллельный перенос в Rn)
Утв:E – измеримо, La(E) – тоже измеримо и m(La(E))=mE
Пусть существует t>0
Рассмотрим преобразование Rt(x)=(tx1,…,txn), X=(x1,…,xn) – растяжение или сжатие по всем координатам. Если Е измеримое, то Rt(E) – измеримо и mRt(E)=tnmE – объем параллелепипеда изменен в tnраз
Пусть существует преобразование Y=MX, которое задается матрицей Mn,n,X=[x1,…,xn] (столбец), M – необязательно невырожденная.
Е – измеримо => ME – измеримо и m(ME)=|det(M)|mE
Если det(M)=0, а mE=, то m(MRn)=0
Образ Rn– пространство меньшей размерности
Если det(M)0, то обратимое линейное преобразование, прямоугольный параллелепипед переходит в косоугольный.
Соотношение измеримости по Лебегу и меры Лебега в пространствах разной размерности
Утв:Мера m(Rn-1x {0})=0
Опр:Пусть существует x2R1,
тогда сечение множества![]() {x1R1:
(x1,xo2)E}
(o– для фиксированности)
{x1R1:
(x1,xo2)E}
(o– для фиксированности)
ТеоремаДля того, чтобы множество E было m2-
измеримо по Лебегу, необходимо и
достаточно, чтобы для m1почти
всюду xo2R1(за исключением множества лежащего на
прямой), множества![]()
были m1- измеримы.
ТеоремаОбщая теорема о соотношении измеримости множества по мере Лебега в различных пространствах
Пусть существует n>k>1
Рассмотрим множество ЕRn
точку XRn, X=(x1,…,xn); X'=(x1,…,xk), X"=(xk+1,…,xn); X=(X',X").
Построим многомерные аналоги для сечения.
Фиксируем точку
X"*Rn-k,
определим множество![]() Rn-k,
Rn-k,
![]() :
(X'
:
(X'![]() <=>(X',X"*)E)
<=>(X',X"*)E)
![]() нумеруется точками из Rn-k, а
само принадлежит Rk, поэтому
определено все Rn
нумеруется точками из Rn-k, а
само принадлежит Rk, поэтому
определено все Rn
Нас интересуют X"*Rn-k: множество проходящие через них будут измеримыми по трем мерам Лебега, в Rn, Rk, Rn-k
Для того, чтобы
множество Е было измеримо по мере Лебега
в Rn, необходимо и достаточно, чтобы
при почти всех mn-kточках X"*,
соответствующее множество
![]() было
измеримо по мере Лебега mk.
было
измеримо по мере Лебега mk.
Теоремао соотношении множества меры нуль и меры больше нуля в пространствах разной размерности.
1) Пусть существует
множество ЕRnи оно измеримо по мере Лебега. Тогда для
того, чтобы mkE>0, необходимо и
достаточно, чтобы mn-kF>0, где
F={X"*Rn-k:
![]() измеримо
и mk
измеримо
и mk![]() >0}
>0}
Эквивалентная переформулировка для множества меры нуль.
Пусть существует
множество АRn,
для того чтобы mnA=0, необходимо и
достаточно, чтобы почти всюду, mn-kX"*, mk![]() =0
(чтобы почти всюду сечения были меры
нуль, по своей мере n-k).
=0
(чтобы почти всюду сечения были меры
нуль, по своей мере n-k).
Индуктивное вычисление меры Лебега ограниченных открытых множеств.
Утв:Функцияf ограничена и непрерывна на любом интервале (ak, bk)prE
Значит она
интегрируема по Риману и справедлива
формула mn+1E=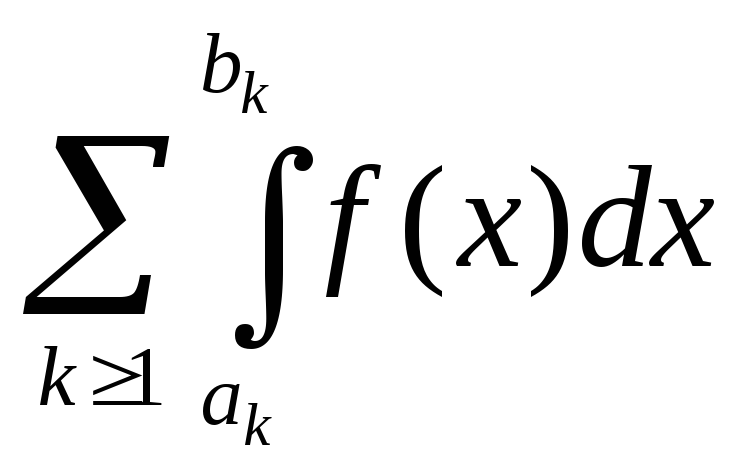
Измеримые функции
Опр:Пусть существует множествоERn, которое измеримо иE
Пусть функция f определена на множествеE. Пустьa – любое вещественное число. Определены 4 множества, которые называются множествами Лебега.
Ea1={xE : f(x)<a}
Ea2={xE : f(x)<a}
Ea3={xE : f(x)>a} все могут быть пустыми
Ea4={xE : f(x)>a}
Функция f называется измеримой, если множестваEak измеримыа, k=1,2,3….
Утв:Еслиa и при каком-либо фиксированом индексеk все множестваEak измеримы, то функцияf измерима.
Свойства:
Пусть
![]() ,
Ek –
измеримо => Е –
измеримо
,
Ek –
измеримо => Е –
измеримо
EmEk=, mk
Пусть f задана наE
1.
f |Ek измеримаk, тоf – измерима наE. f, суженная наEm
f измерима наE, тоf |Ek измерима наk
2. Пустьf(x)=c, xE, E- измеримо, тогдаf(x) – измеримая
3. Множество E разбито на счетную совокупность измеримых множеств.
f |Ek=ck, тогдаf измеримо
Важные примеры измеримых функций
Пусть GRn либо открытое, либо основное,G
Пусть f ограничено и непрерывно наG, тогда она измерима наG.
Связь измеримости функций в пространствах разного числа переменных
Пусть существует ERn , 1<k<n, E – измеримо вRn
x=(x', x"), x'=[x1,…,xk], x"=(xk+1,…,xn)
![]() ={x'Rn
: (x', x"0)E
– сечение
={x'Rn
: (x', x"0)E
– сечение
на Е определена некая функция f
если взять
фиксированный x"0
, то можно рассмотреть![]() (x')=f(x',x"0)
приx'
(x')=f(x',x"0)
приx'![]() ,
если
,
если![]() ,
то иf=0, иначеf
функция лежащая в пространстве
меньшей размерности.
,
то иf=0, иначеf
функция лежащая в пространстве
меньшей размерности.
Ea1(![]() )=
)=![]() если рассмотрим сужение функции
наE и рассмотрим точку,
где она<a, это<=>
если рассмотреть все множество, где
функция< a и рассмотрим
сечение этих множеств.
если рассмотрим сужение функции
наE и рассмотрим точку,
где она<a, это<=>
если рассмотреть все множество, где
функция< a и рассмотрим
сечение этих множеств.
Арифметические действия над измеримыми функциями
ERn – измеримо
f – измеримо,k – const => kf – измерима,k=0 – неверно.
f – измеримо => | f | измеримо (но не<=)
f(x)0xE – измерима=> 1/f – измерима
f – измерима => f2 – измерима
Пусть f,g измеримы наE => f+g измерима наE.
Пусть существует f1,…,fk – измеримо => с1f1+…+ckfk – измеримы
Пусть f,g – измеримы => fg – измерима
Пусть существует f1,…,fk – измеримы => f1f2f3…fk, в частностиfn – измерима
![]() - измеримыf(x)0
- измеримыf(x)0
f(x)0 и измерима,g – измерима => g/f – измизмерима
Эквивалентность функций
Пусть существует ERn измеримы
f,g – функции заданные на Е
Будем говорить, что f,g – эквивалентны(f~g), еслиGE : XG<=>f(x)g(x), еслиmG=0
f~g, g~h => f~h.
Пусть HE, g(x)h(x) => mH=0
GH – объединение множеств меры нуль => m(GH)=0
K : f(x)рр
h(x) KGH => mK=0 (K - точка )
Утв: Еслиf – измерима иf~g, тоg – измерима.
Утв:ПустьE – измеримо,f,g – заданы наE
g~f и заданы числаa<b
Рассмотрим множества: m(Eb2(f)Ea3(f))< - конечно =m(Eb2(g)Ea3(g))<
Kf={a<f(x)<b}
Kg={ a<f(x)<b}
Действия над эквивалентными функциями дают эквивалентные функции.
Интеграл Лебега
Интеграл Лебега по множеству конечной меры от ограниченной, измеримой функции.
ERn E – измеримой иmE<
Пусть f определена на Еf – измерима и ограничена. СуществуютA,B : A<f(x)<B
Опр: Верхние и нижние суммы Лебега.
Считаем, что A,B – определены
Разобъем промежуток A,B на интервалы (разбив множество значащих функций).
S : A=S0<S1<…<Sk=B
Ek(S)={xE : Sk-1<f(x)<Sk} k=1,2,…,n
Ek(S)=ESk-1(f)ESk,2(f) – измеримо
Любое Ek(S) является измеримым (м/б пустым)Ek(S)El(S), kl, т.к. еслиk<l, тоf(x)<Sk иf(x)>Sl-1
Ek(S)E => mEk(S)<+
![]() - по свойству аддитивности
- по свойству аддитивности
mE![]() (1)
(1)
верхние суммы Лебега L+(f,S), нижние– L-(f,S)
L+(f,S)![]()
L-(f,S)![]()
Свойства:
A<Sk-1<Sk<B (приk=1 S0=A)
AmE<L-(f,S)<L+(f,S)<BmE (2)
S, A=S0<…<Sk=B
![]() ,
Si-1<<Si
– добавим точку
перенумеровывать не будем
,
Si-1<<Si
– добавим точку
перенумеровывать не будем
Ei(S) Si-1<f(x)<S
E'i(S) {xE : Si-1<f(x)<}
E''i(S) {xE : <f(x)<Si}
Ei(S)=E'i(S)E"i(S)
mEi(S)=mE'i(S)+mE"i(S)
Рассмотрим разность сумм Лебега
L-(![]() )-L-(S)=Si-1mEi'(S)+mEi"(S)-Si-1mEi(S).
(все остальные слагаемые одинаковые,
сокращаются)>
)-L-(S)=Si-1mEi'(S)+mEi"(S)-Si-1mEi(S).
(все остальные слагаемые одинаковые,
сокращаются)>
>Si-1mEi'(S)+Si-1mEi"(S)-Si-1mEi(S)=0
аналогичное
доказательство, что L+(S)-L+(![]() )>0,
т.е. получим, что если добавляем 1
точку, то
L-(S)<L-(
)>0,
т.е. получим, что если добавляем 1
точку, то
L-(S)<L-(![]() )<L+(
)<L+(![]() )<L+(S)
)<L+(S)
Пусть SS* (как множество), тоL-(S)<L-(S*)<L+(S*)<L+(S)
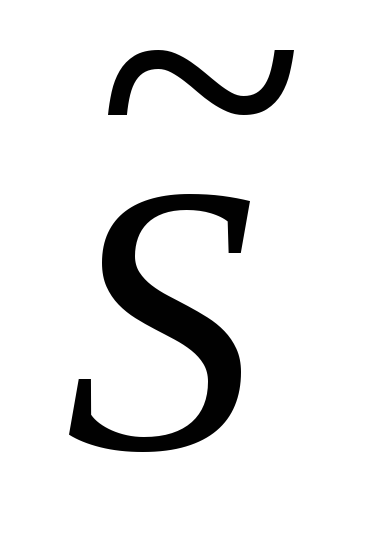 ,S L-(S)<L+(
,S L-(S)<L+(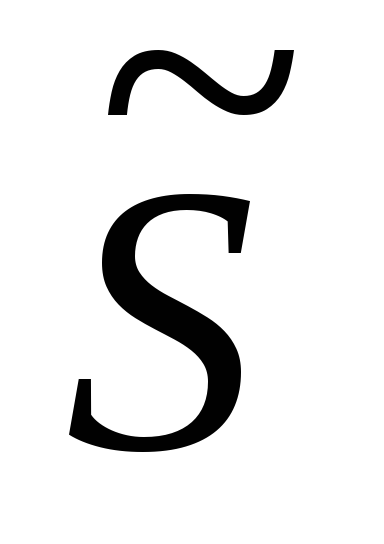 )
)
т.о. нижняя сумма Лебега< верхней суммы Лебега
введем: I*=supS L-(S)
I*=infS L+(S) => I*<I* (3)
Теоремав рассмотренной ситуацииI*=I*
Общее значение I*=I*=I называется интегралом Лебега от функцииf по множествуE ипо мере Лебега.
Интеграл Лебега существует для множества конечной меры и функции измеримой и ограниченной.
I=![]()
Свойства интеграла Лебега
E – измеримо, мераE конечна
f,g –
ограничены,f~g, f,g –
измеримы, тогда
![]() =
=![]()
f0(x)=c0 xE =>
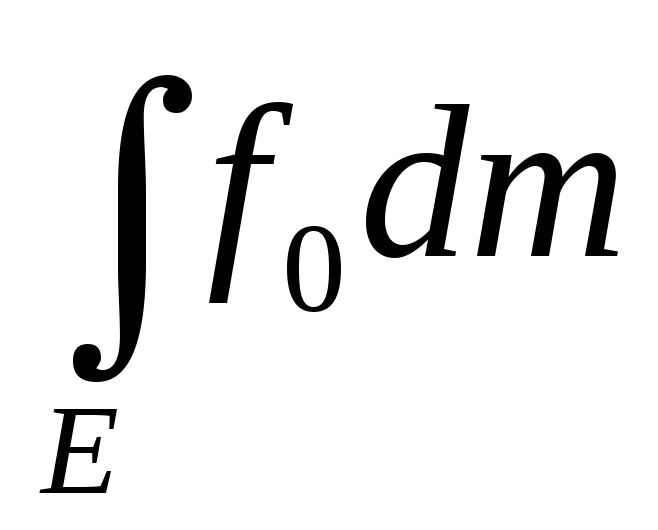 =с0mE
=с0mE
2.'
f1~c0
может отличаться отc0
на множестве меры нуль, то
![]() =с0mE
=с0mE
2."
f2~0,
то
![]() =0
=0
Пусть E : mE=0, тогда
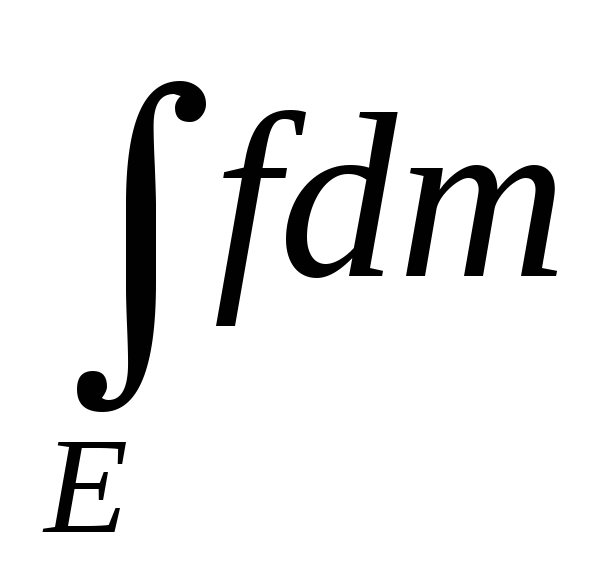 =0f
=0fПусть
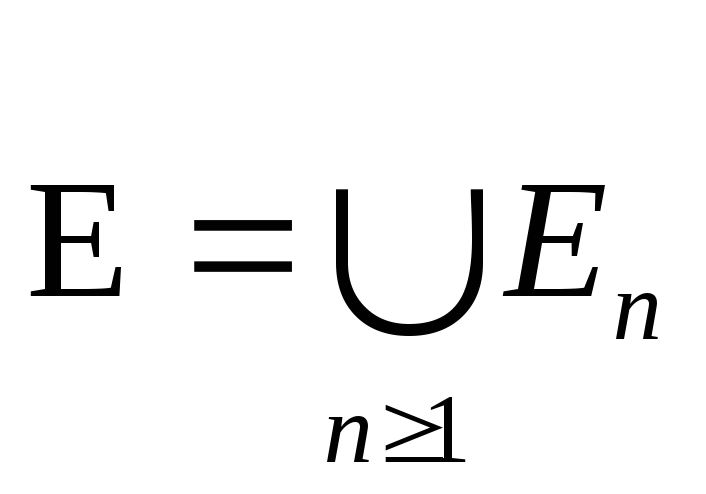 ,
En –
измеримое, ограниченное =>
E – ограниченноEnEm=,
nm
,
En –
измеримое, ограниченное =>
E – ограниченноEnEm=,
nm
f –
измеримо наE (=>
измеримоEn
=> существуетEn
иcуществуетE),
тогда выполняется соотношение
![]() =
=![]() (3)
(3)
если множество конечное число, то сумма, если счетное, то сумма ряда и этот ряд сходится абсолютно. Свойство 4 называется счетной адитивностью
4.' Пусть выполняется условие 4 дляE, En
Пусть f~Cn
приxEn,
A<Cn<B
n,
тогда
![]() =
=![]()
A<f(x)<B
Возьмем A1, B1 : A1<f(x)<B1 получится тоже самое
A<A1, A2=max(A,A1)
Si<A1, тоEi(f,S)=
Пусть f
измерима, ограничена наE
и выбраны такие точкиA1,
B1.
Тогда
![]() ,
построенные по[A,B) ; [A1,
B1)
совпадают.
,
построенные по[A,B) ; [A1,
B1)
совпадают.
Пусть f(x)>c0 xE
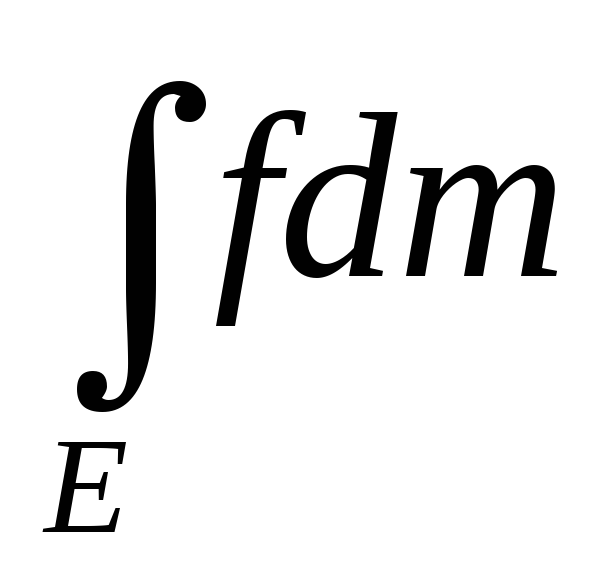 >c0mE
>c0mE
Пусть f(x)<c1,
![]() <c1mE
<c1mE
6.'
![]() =k
=k![]() ,
дляk0
,
дляk0
|
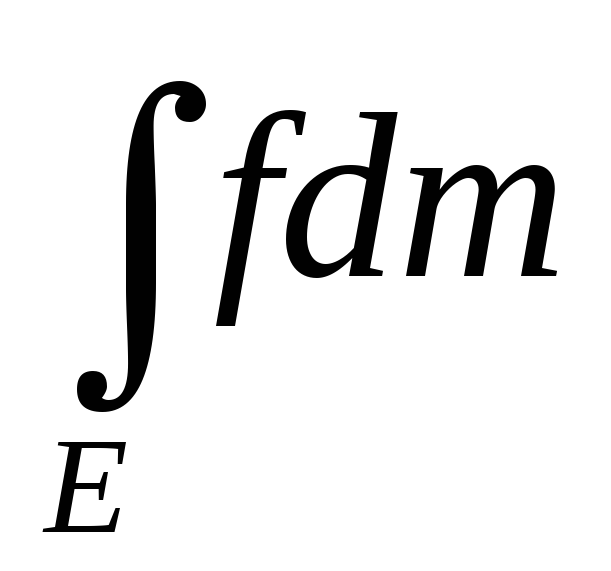 |<
|<
 =
=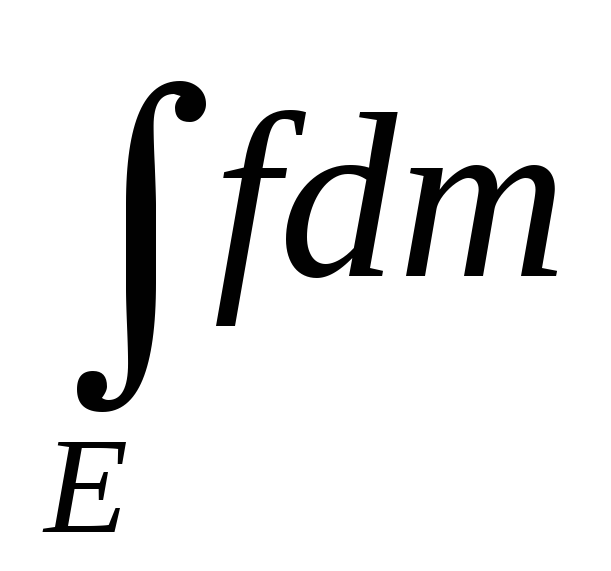 +
+
Пусть f>g =>
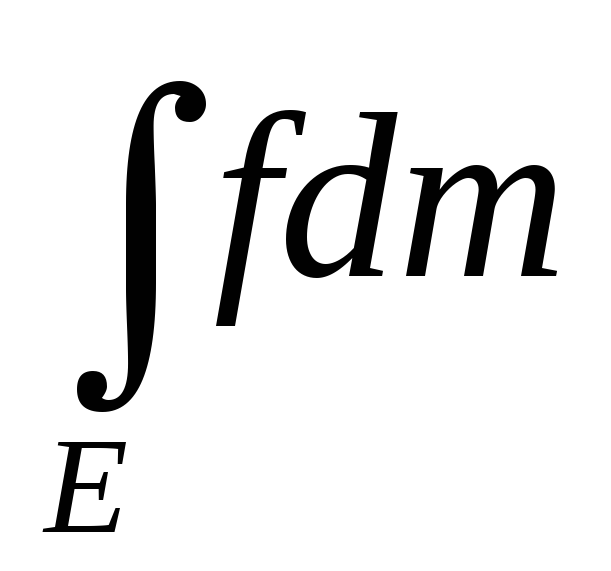 >
>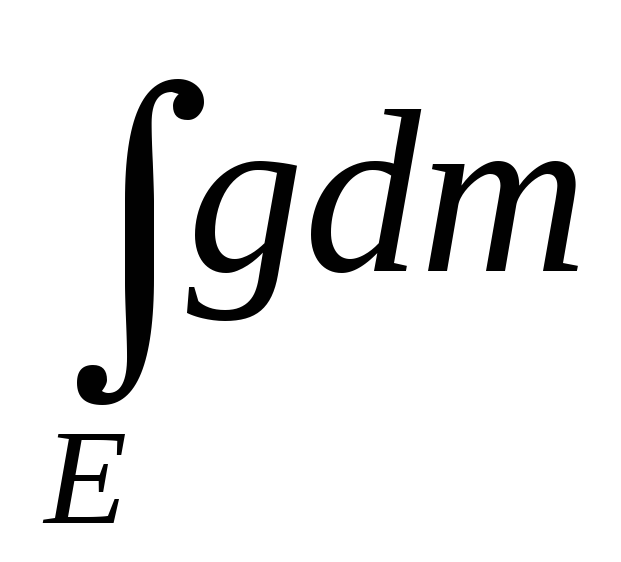
Пусть f>g и
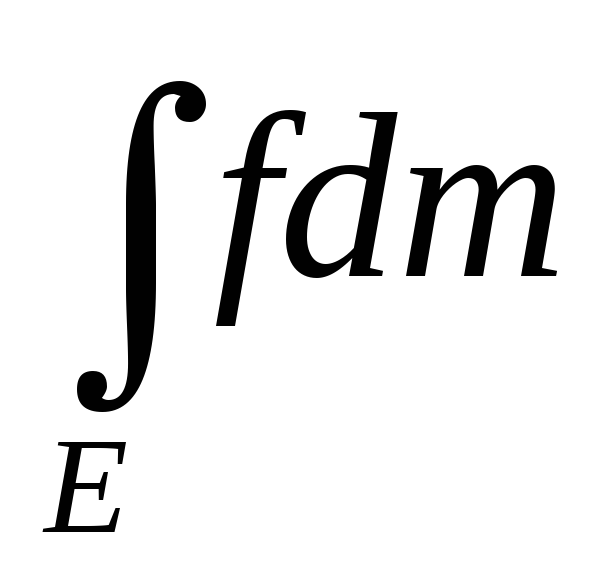 =
=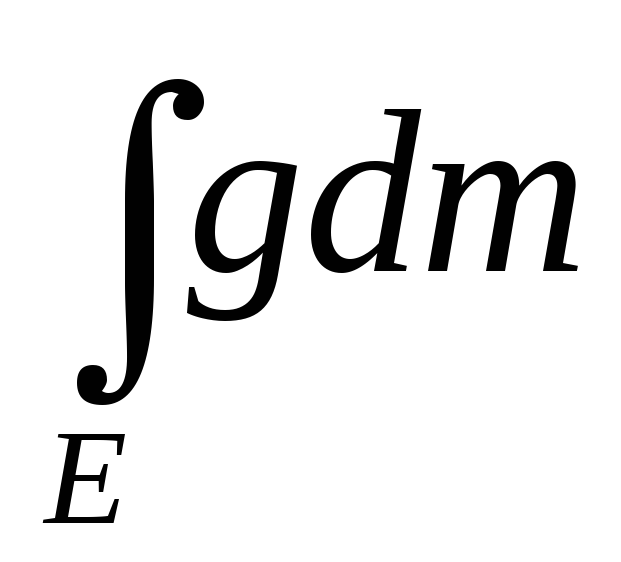 ,
тогда f~g
,
тогда f~g
10.'
f>0 и
![]() =0
=> f~0
=0
=> f~0
Связь между интегралом Римана и интегралом Лебега
Пусть функция интегрируема на (a,b) по Риману, тогда она измерима по Лебегу.
![]() =
=![]()
11.' Существенное дополнение к теории интеграла Римана.
Для того, чтобы функция f измеримая и ограниченая на (a,b) была интегрируема по Риману на (a,b) необходимо и достаточно, чтобы в почти каждой точки(a,b) она была непрерывна.
Распространение теории интеграла Лебега на неограниченные измеримые множества.
Пусть ERn mE<
Пусть существует E, функцияf измерима на Е
fl(x)={f(x) : |f(x)|<l ; 0 : |f(x)|>l}, множество{f(x)>l}B{f(x)<-l} – измеримо
|fl(x)|<min
(l,|f(x)|) – множествоE –
конечной меры, можно написать![]() =al
=al
Опр:Говорят, что функцияf суммируема на множествеE, еслиal<cf l>0
Ограниченность
означает, что существует конечный предел
: существует
![]() ,
,
![]() =a+
=a+
Теорема Для суммируемых функций справедливы следующие свойства:
Рассмотрим множество E+ : {XE : f(x)>0}, по свойству 4 ИЛ, из суммируемостиf наE => суммируемостьf наE+, гдеxE : |f(x)|=f(x)
![]() =
=![]()
Рассмотрим множество E_ : {XE : f(x)<0}, по свойству 4 ИЛ, из суммируемостиf наE => суммируемостьf наE_, гдеxE : |f(x)|=-f(x) ; f(x)=-|f(x)|
![]() =
=![]()
Если f
суммируема наE, то по
определению
![]() =
=![]() =
=![]()
Распространение интеграла Лебега на множества бесконечной меры для измеримой функции.
Пусть существует ERn, ноmnE=+
Пусть существует f измеримая наE
Рассмотрим шар BR={||x||<R} иER=EBR
Пусть f
суммируема на любомER,
определим функцию на полуосиl(R)=
![]()
Опр:
Говорят, что функцияf
суммируема на множествеE,
если функцияl(R) ограничена,
т.е. существуетCf'
: l(R)<
Cf'
R,
тогда (по теореме о существовании
предела монотонной функции) существует
конечный предел:
![]() ,
полагаем
,
полагаем
![]() =l(+)
=l(+)
Утв:Для суммируемых функций на множестве бесконечной меры справедливы свойства1-10
ТеоремаФубини
Пусть существует ERn, 1<k<n
f – измерима, суммируема на Е
Пусть x'=(x1,…,xk) – первыеk координат
![]() ={yRn-k
: (x0',y)E},
тогда при почти всехx0'
функцийf суженная на
={yRn-k
: (x0',y)E},
тогда при почти всехx0'
функцийf суженная на
![]() суммируема
по (n-k) мерной мере Лебега
и верна формула:
суммируема
по (n-k) мерной мере Лебега
и верна формула:
![]() =
=![]()
Понятие пространств Lp
Пусть существует E – измеримо иmE>0, p>0
LP(E) состоит из всех таких функцийf измерима наE
для которых
|f(x)|P
суммируем на множествеE,
значит определен
![]() <+
<+
p=1
L1(E) состоит из всех функций суммируемых на Е, далее будем рассматривать1<p<+
![]() =0
<=> f0~0
=0
<=> f0~0
Если fLP(E),
то
![]()
Теорема Неравенство Минковского (1<p<)
f,gLP(E)
в.с.
![]()
Некоторые концепции теории рядов Фурье с точки зрения интеграла Лебега
Пусть E = (-,)R1, рассмотрим функции f, суммируемые на E, тогда мы можем рассмотреть f(x)cos(nx) и f(x)sin(nx), также суммируемых на E.
тогда можно определить коэффициенты Фурье суммируемой функции.
(1)
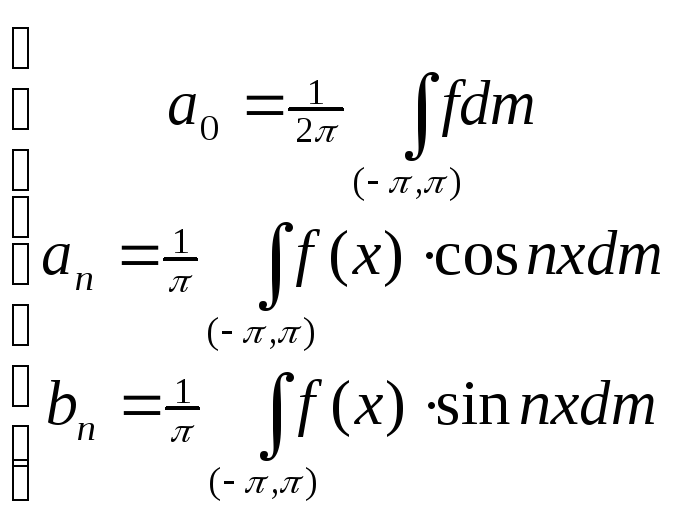
Если f~0, тогдаa0=an=bn=0
ТеоремаПринципиальная теорема, обратная к соотношению (2)
Пусть f измерима на (-,), которая суммируема на этом множестве, построим по ней коэффициенты Фурье по формуле (1)
Предположим, что a0=an=bn=0 n, тогдаf
Равенство Парсеваля
Лемма: Пусть mE< и пусть1<p1<p2 => LP2(E)LP1(E) в частностиL2(-,)L1(-,)
Пусть a0, an, bn – коэффициенты Фурье,fL2(-,), тогда верно
![]() =
=![]() <+
<+
ТеоремаРисса-Фишера
Пусть A0,
An, Bn
удовлетворяет условию
![]() <+,
тогда существует функцияgL2(-,)
: ее соответствующие коэффициенты
Фурье совпадают сA0,
An, Bn
<+,
тогда существует функцияgL2(-,)
: ее соответствующие коэффициенты
Фурье совпадают сA0,
An, Bn
