Предгильбертовы пространства.

Определение: Пусть есть линейное пространство ( R или С) L. Это пространство будем называть Предгильбертовым, если определены операции скалярного произведения:

Для  xL и  yL:

(x,y) R (или C)

и эти операции обладают следующими свойствами:

Вещественные	Комплексные
(x,x)0	(x,x)0
(x,x)=0 <=> x = 	(x,x)=0 <=> x = 
(x1+x2,y) = (x1,y)+(x2,y) (x,y1+y2) = (x,y1)+(x,y2)	(x1+x2,y) = (x1,y)+(x2,y) (x,y1+y2) = (x,y1)+(x,y2)
(ax,y)=a(x,y)  aR (x,ay)=a(x,y)  aR	(ax,y)=a(x,y)  aC (x,ay)=(x,y)  aC
(y,x)=(x,y)	(y,x)=

Норма в Гильбертовом пространстве

Утверждение: Пусть L – вещественное или комплексное гильбертово пространство, тогда норма x:

||x|| =

Лемма: Справедливо |(X,y)|||X||*||y||

Определение: Пусть есть предгильберово пространство вещественное или комплексное. Если оно является полным относительно нормы, то оно называется гильбертовым пространством.

Ортогональное разложение гильбертова пространства.

Определение: Пусть H – гильбертово пространство, x,yH – называются ортогональными, если (x,y) = 0.

Утверждение: Пусть H₁ H, H₁  {}, H₁  H.

Тогда существует y₀H₁, y₀H₁, такое что:

(y₀,x) = 0 xH₁.

Определение: множество всех y₀{ }H, удовлетворяющих приведенному выше условию, будем обозначать H₁^.

Утверждение: Линейное пространство H₁^ оказывается полным относительно нормы, введенной с помощью скалярного произведения, употребляемой на всем пространстве. Это линейное пространство называется ортогональным дополнением подпространства H₁ и само является подпространством.

Ортогональные ряды в гильбертовом пространстве

Определение: Рассмотрим ряд x_n , где x₁, x₂,… x_n… H.

Этот ряд называется ортогональным рядом, если n,m: n#m справедливо:

(x_n,x_m) = 0.

Теорема: Пусть имеется ортогональный ряд, тогда его элементы линейно независимы.

Лемма: Пусть есть гильбертово пространство H и x₁, x₂,… x_n… H, причем x_k#0 k и (x_k,x_l) = 0 ( для k,l: k # l).

Тогда они ЛНЗ.

Определение: Гильбертово пространство H будем называть конечномерным, если:  N: любые x₁, x₂,… x_N, где x_j # 0 для j – линейно независимы.

Определение: Пусть есть H₁,H₂ – гильбертовы пространства. Будем называть их изометричными, если:

• они изометрично изоморфны как банаховы пространства.

• A: H₁H₂ и x,yH₁ выполняется:

(Ax,Ay)_H2 = (x,y)_H1.

Теорема: Всякое конечномерное Гильбертово пространство, изометричное пространству Rⁿ, изометрично пространству Cⁿ.

Определение: Гильбертово пространство, которое не является конечномерным, называется бесконечномерным.

Определение: Пусть есть H – бесконечномерное Гильбертово пространство, тогда для любого n  x₁, x₂,… x_n, (где x_k#0 k)

1. ||x_k|| = 1 (k)

2. (x_k,x_l) = 0 ( для k,l: k # l).

V_n - множество x₁, x₂,… x_n. Будем называть V_n – конечной ортонормированной системой.

А a_k = (по опред) = (y,x_k) – это k-й коэффициент ряда Фурье.

Неравенство Бесселя.

Пусть V_{n -} конечная ортонормированная система из элементов x₁, x₂,… x_n, a_k - k-й коэффициент ряда Фурье, тогда:

|a₁|² + |a₂|² +…+ |a_n|²  ||y||².

Определение: Пусть есть H -гильбертово пространство и есть EH. Будем говорить, что мрожество полно в гильбертовом пространчтве, если из условия (x,a) = 0 (для aE) следует x = 0.

Утверждение: Пусть E – всюдуплотное множество в H, тогда E – плотно в H.

Следствие: Если H – сепарабельное Гильбертово пространство, то в нем существует счетное плотное множество.

Теорема: Во всяком сепарабельном Гильбертовом пространстве существует конечная или счетная полная ортонормированная система. При этом она оказывается конечной, если пространство конечно, и оказывается бесконечной, если пространство бесконечное.

Определение: Пусть L – пространство x₁, x₂,… x_mL. Линейной оболочкой Z(x₁, x₂,… x_m) этих элементов будем называть множество комбинаций:

{c₁x₁+c₂x₂+ … +c_mx_m R (или C)}.

Лемма: Если мы рассмотрим линейную оболочку любого конечного числа элементов в пространстве H, то эта линейная оболочка является поным подмножеством в H.

Теорема замкнутости: (Равенство Парсеваля):

Пусть есть H – Гильбертово пространство (сепарабельное, бесконечномерное) и l₁,l₂,…l_n… - полная ортонормированная система, тогда:

a_n = (x,l_n) ,  xH

b_n = (y,l_n) ,  yH

и выполняется:

1)

при этом:

3. 

Определение: Пусть есть H - Гильбертово пространство ( сепарабельное и бесконечномерное). Система f_nH. Для  xH  a_n (и единственное) (a_nC):

Такая система называется базисом в H.

Вывод: Итак, нами доказано, что полная ортогональная система в любом сепарабельном бесконечномерном пространстве существует и является базисом в этом пространстве.

Структурная теорема о сепарабельном бесконечномерном простанстве: Всякое вещественное сепарабельное бесконечномерное Гильбертово пространство H изометрично l_R², а всякое комплексное сепарабельное бесконечномерное Гильбертово пространство изометрично l_C².

Каноничная инволюция в H.

Пусть есть H (сепарабельное б/мерное Гильбертово пространство) и {l_n} – его ортонормированная система. Тогда  xH:

Утверждение: Каноническая инволюция Jx – не зависит от выбора {l_n}.

Свойства Jx: 1) J(x+y) = Jx+Jy.

2)  cC: J(cx) = Jx

Описание сопряженного комплексному бесконечномерному сепарабельному Гильбертову пространству.

H – Гильбертово пространство. Рассмотрим H*: Пусть y*H*, xH, тогда

(y*,x) – линейный функционал y*, действующий на x.

Пусть {l_n}^_n=1 – полная ортонормированная система.

(y*,x) = (y*,a_nl_n) = (y*,a_nl_n) = a_n(y*,l_n)

Определение: Положим _n = (y*,l_n).

Лемма: Пусть _n = (y*,l_n), тогда справедливо:

Элементы спектральной теории операторов.

Пусть H – комплексное Гильбертово пространство, и есть линейный ограниченный оператор T: HH.

TT = T²: HH

TT…T = Tⁿ: HH.

P(z) = a₀+a₁z+…+a_nzⁿ.

A = P(T) = a₀I+a₁T+…a_nTⁿ.

Рассмотрим другой полином: q(z) и q(T).

Когда P(T) = q(T) при Pq?

Пусть есть T: HH. Существует ли B: HH, такой что T = B²?

Рассмотим конечномерное Гильбертово пространство Cⁿ:

и есть T: Cⁿ Cⁿ, ему можно сопоставить матрицу:

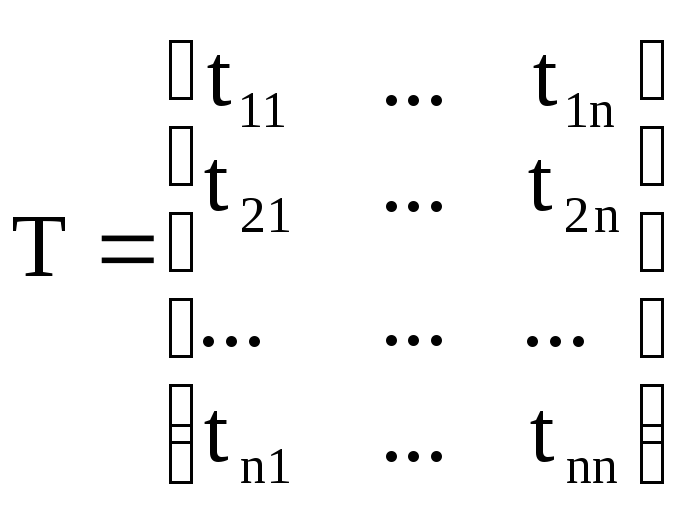
TZ =

T²  ² и понятно, что T^K  ^K

Пусть есть два многочлена p и q, p # q. Введем r = p-q. Если p # q, то r # 0. Если же p = q (как операторы), то r = 0. (1)

С матрицей T можно связать характеристический многочлен ():

Теорема Кэли: Для того, чтобы выполнялось (1) необходимо и достаточно, чтобы существовал многочлен k(): r() = () k() (2)

Где () – характеристический многочлен для матрицы T, r() - характеристический многочлен для разности, т.е, если (1)<=>(2), то

(T) = 0, r(T) = 0.

То есть вопрос в делимости r() на ().

Определение: Комплексное число  будем называть регулярной точкой оператора T, если оператор ^-1I-T имеет обратный оператор.

Определение: Если  - регулярная точка оператора T, тогда резольвентой оператора T в точке  будем называть обратный оператор R(^-1,T) = (^-1I-T)^-1. При этом выполняется: (^-1I-T) R(^-1,T) = R(^-1,T) (^-1I-T) = I.

Определение: Множеством всех регулярных точек называется регулярным или резольвентным множеством. Обозначается (T).

Утверждение: Если H – конечномерно и ₁,… _n – различные собственные числа оператора T, то (T) = С\ .

Определение: Спектром оператора T (T) – называется: (T) = С\(T) – множество всех резольвентых точек:

(T) =

Принципиальная теорема о спектре оператора и его резольвенте: Резольвентное множество оператора непусто и открыто. Спектр оператора замкнут и непуст.

Лемма: Оператор R_N = ^-1I + - образует фундаментальную последовательность в банаховом пространстве.

Вполне непрерывные компактные операторы.

Определение: Пусть имеется T: HH, где H – бесконечномерное сепарабельное Гильбертово пространство. Будет называть T – компактом, если:

x_nH: ||x_n||  M (n)

из последовательности Tx_n можно выбрать сходящуюся подпоследовательность.

Теорема: Спектр компактного оператора не имеет С точек сгущения, кроме возможно, точки 0.

Определение: Ненулевой элемент x_j, удовлетворяющий соотношению Tx_j = x_j, называется собственным элементом оператора T.

Операторы, сопряженные по Гильберту.

Определение: Гильбертовым сопряженным к А мы будем называть такой оператор А_*: А_*: НН, такой что x,yH:

(Ax,y) = (x,A_*y).

Теорема: Гильбертов сопряженный оператор к линейному оператору А существует, единственен и является линейным оператором А_*: НН.

Теорема: || А_*|| = ||A||.

Существенное свойство: (A_*)_* = A.

Определение: Оператор A: HH – самосопряженный, если А_* = А. Тогда справедливо: (Ax,y) = (x,Ay).

Важное наблюдение: Пусть А – самосопряженный оператор в Гильбертовом пространстве, тогда:

(Ax,y) = (x,Ay) = .

Теорема: Пусть А – самосопряженный оператор в Гильбертовом пространстве, тогда спектр оператора А – вещественный и принадлежит области [-||A||, ||A||].

Положительно определенные операторы.

Определение: Пусть А – самосопряженный оператор в Гильбертовом пространстве. А – положительно определенный оператор, если  m>0, не зависящее от x, такое, что:

(Ax,x)  m||x||², xH.

Уточнение из предыдущей теоремы: Если А – положительно определенный оператор, то (A) [m, ||A||], где m – см. выше.

Непрерывные банаховозначные функции и интегралы от них.

Определение: Пусть Г – непрерывная кривая, ГС, и В – Банахово пространство. Будем говорить, что у нее на Г определена банаховозначная функция от t – F(t), если:

1. tГ => F(t) B.

2. t₀Г || F(t) – F(t₀)||_{B t0}  0.

Суммой Римана для F(t) будем называть S_n = .

Утверждение: Элементы I_n образуют фундаментальную последовательность в В, если max _k| t_k – t_k-1|_n0.

Определение: = по определению = I, которое взято см. выше.

Две важные функции от ограниченных операторов.

Теорема: Оператор T_n = - образует фундаментальную последовательность в банаховом пространстве, т.е. ||T – T_n|| _n0.

Утверждение: e^A = T - по определению и справедливо || T ||  e^||A||.

Корень квадратный из положительно определенного оператора.

Пусть А: НН - положительно определенный оператор, тогда (Ax,x)  m||x||².

Рассмотрим Г – эллипс, лежащий строго в правой полуплоскости и содержащий m и ||A||. Для всякого Г существует резольвента R(,A) Y и   R(,A) Y.

Пусть В = - некоторый интеграл в Y.

Утверждение: В – является линейным непрерывным оператором: НН и В² = А.