
- •Глава 1:введение в анализ.
- •U – высказывание.
- •Параграф 5: последовательность. Точка. Предел последовательности.
- •Параграф 6: предел последовательности.
- •Параграф 7: бесконечно малые величины.
- •Параграф 8: бесконечно большие величины.
- •Леммы о бесконечно больших.
- •Параграф 9: теоремы о пределах.
- •Параграф 10:предел функции
- •Параграф 11: одностороние пределыслева и справа точки .
- •Параграф 12: предел функции на бесконечности.
- •Определение предела функции на бесконечности на языке окрестностей.
- •Параграф 13: замечательные пределы.
- •Формулы гиперболической тригонометрии.
- •Параграф 14: взаимные пределы, основанные на втором замечательном пределе.
- •Параграф 15: сравнение бесконечно маленьких.
Параграф 10:предел функции
Опр. 1:Постоянное число
![]() называется пределом функции
называется пределом функции
![]() при
при
![]() ,
если для любого
,
если для любого
![]() существует число
существует число
![]() ,
такое, что при выполнении неравенства
,
такое, что при выполнении неравенства
![]() следует выполнение неравенства
следует выполнение неравенства
![]() .
.
![]() или
или![]()
Запишем неравенство (1)и(2)без модуля:
![]()
![]()
Двойное неравенство (3) определяет
![]() – окрестность точки
– окрестность точки
![]() на оси абсцисс.
на оси абсцисс.
Двойное неравенство (4)определяет
![]() – окрестность точки
– окрестность точки
![]() на оси ординат.
на оси ординат.
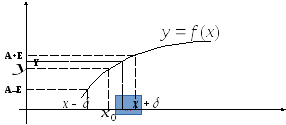
Определение предела функции означает,
что по выделенной производной
![]() – окрестности точки
– окрестности точки
![]() на оси
на оси
![]() определяется
определяется
![]() – окрестность. Есть точка
– окрестность. Есть точка
![]() на оси
на оси
![]() такая, что как только переменная
такая, что как только переменная
![]() попадает в
попадает в
![]() – окрестность своей предельной точки
– окрестность своей предельной точки
![]() ,
так сейчас же переменная
,
так сейчас же переменная
![]() попадает в
попадает в
![]() – окрестность своего предельного
значения
– окрестность своего предельного
значения
![]() .
.
Замечание
В определении предела указывается, что
![]() т. к. в точке
т. к. в точке
![]() функция может быть не определена.
функция может быть не определена.
Все теоремы о пределах, сформулированные
и доказанные для случая переменной
![]() ,
т. е. последовательности, переносятся
без существенных изменений на случай
предела функции.
,
т. е. последовательности, переносятся
без существенных изменений на случай
предела функции.
Параграф 11: одностороние пределыслева и справа точки .
Сформулированное определение предела
в предыдущем параграфе относится к так
называемому двустороннему пределу, что
означает, что переменная
![]() приближается к своему предельному
значению с любой стороны, и слева, и
справа. В некоторых случаях двусторонний
предел может не существовать, но
существуют односторонние пределы, когда
переменная
приближается к своему предельному
значению с любой стороны, и слева, и
справа. В некоторых случаях двусторонний
предел может не существовать, но
существуют односторонние пределы, когда
переменная
![]() приближается к
приближается к
![]() только с одной стороны, или слева, или
справа. В этом случае указывается
соотношение
только с одной стороны, или слева, или
справа. В этом случае указывается
соотношение
![]() или
или
![]() .
.
Запись
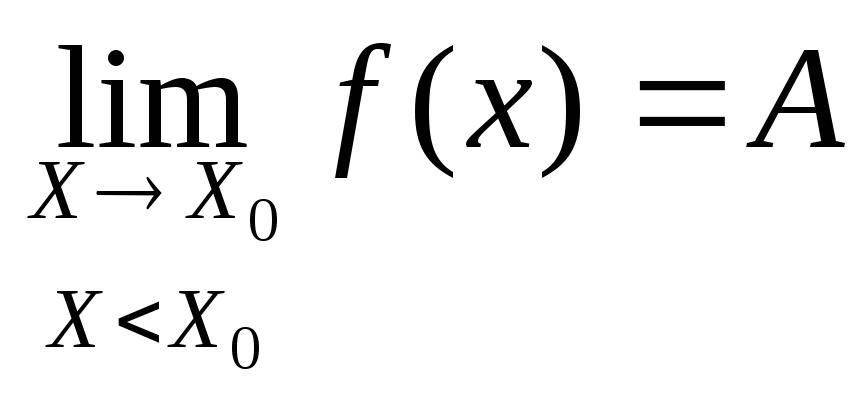 – предел слева.
– предел слева.
 – предел справа
– предел справа
Второй вариант записи:
![]() – предел слева.
– предел слева.
ТЕОРЕМА:
Для того, чтобы в точке
![]() существовал двусторонний предел функции,
необходимо и достаточно, чтобы существовали
оба односторонних предела и они были
равны между собой:
существовал двусторонний предел функции,
необходимо и достаточно, чтобы существовали
оба односторонних предела и они были
равны между собой:
![]()
Параграф 12: предел функции на бесконечности.
Опр. 1:Постоянное число
![]() называется пределом функции
называется пределом функции
![]() при
при
![]() ,
если для любого
,
если для любого
![]() можно указать число
можно указать число
![]() ,
что при выполнении неравенства
,
что при выполнении неравенства
![]() ,
следует выполнение неравенства:
,
следует выполнение неравенства:
![]() .
.
Заменим неравенства (1) и (2) без модуля:
![]()
![]()
![]()
Геометрическая интерпретация определения предела:

Неравенство (1)или(1а) определяет
так называемую
![]() – окрестность бесконечности.
– окрестность бесконечности.
![]() .
.
Если функция
![]() имеет предел на бесконечности равное
имеет предел на бесконечности равное
![]() ,
то график функции
,
то график функции
![]() имеет горизонтальную асимптоту.
имеет горизонтальную асимптоту.
Определение предела функции на бесконечности на языке окрестностей.
Постоянное число
![]() называется
пределом функции при
называется
пределом функции при
![]() ,
если для любой
,
если для любой
![]() – окрестности точки
– окрестности точки
![]() на оси
на оси
![]() существует
существует
![]() – окрестность бесконечности на оси
– окрестность бесконечности на оси
![]() такая, что как только аргумент
такая, что как только аргумент
![]() попадает в
попадает в
![]() – окрестность бесконечности, так сейчас
же функция
– окрестность бесконечности, так сейчас
же функция
![]() попадает в
попадает в
![]() – окрестность точки
– окрестность точки
![]() .
.
ПРИМЕР:

График имеет асимптоту горизонтальную
![]() .
.
Общее определение предела на бесконечность сохран., но дополняет указанный знак бесконечности. Все теоремы о пределах для всех модификаций определения предела сохраняются.
Параграф 13: замечательные пределы.
I.![]()

Функция
![]() – четная, поэтому можно ограничится
только положительными значениями
– четная, поэтому можно ограничится
только положительными значениями
![]() и т. к.
и т. к.
![]() ,
то можно ограничится значениями
,
то можно ограничится значениями
![]() в первой четверти, т. е.
в первой четверти, т. е.
![]() .
Рассмотрим площади трех фигур:
.
Рассмотрим площади трех фигур:
![]() .
.
 .
.
![]() – радианная мера угла.
– радианная мера угла.
![]()
Т. к. фигуры вложены друг в друга, то их площади связаны неравенством:

Из неравенства (2) вытекает, что при
![]()
![]() ,как
меньшая величина, тоже стремиться к
нулю. Из формулы (*) следует, что
,как
меньшая величина, тоже стремиться к
нулю. Из формулы (*) следует, что
![]() при
при
![]() .По
теореме о сжатой переменной и по формуле
(3) заключаем, что
.По
теореме о сжатой переменной и по формуле
(3) заключаем, что
![]() при
при
![]() .
.
 .
.
ПРИМЕРЫ:
1. 
![]()
2. ![]()
![]()
![]()
Формула (4) записана иначе:

II.Второй замечательный предел.
ОПРЕДЕЛЕНИЯ:
Переменная
 называется возрастающей в узком смысле
(строго возрастает), если при
называется возрастающей в узком смысле
(строго возрастает), если при
 следует
следует
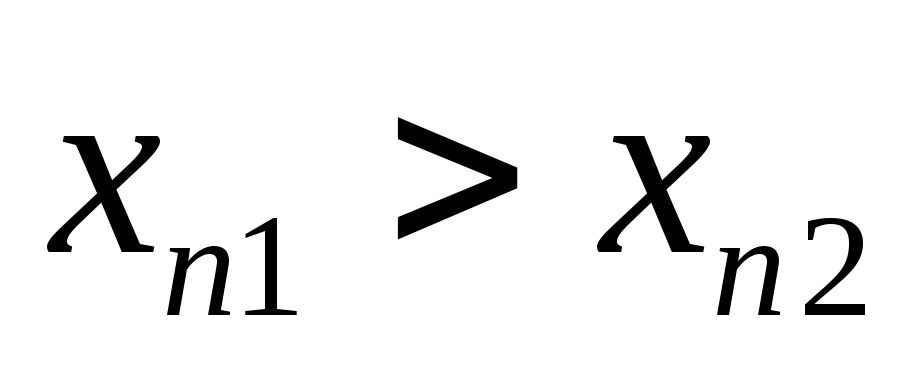 .
.Переменная
 называется строго убывающей, если при
называется строго убывающей, если при
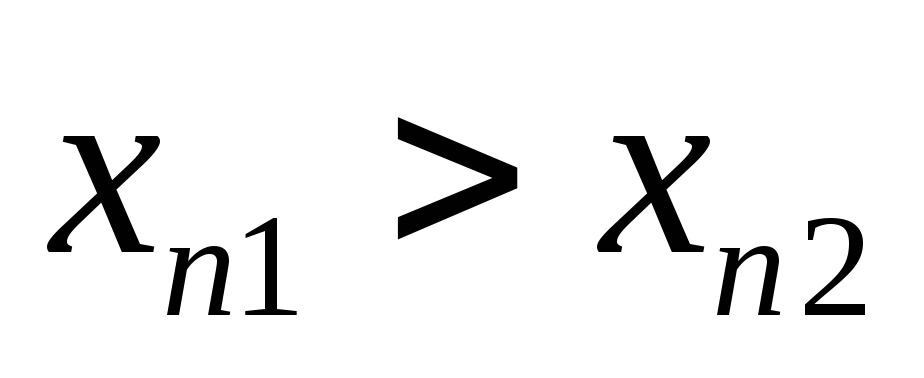 следует
следует
 .
.Переменная
 называется возрастающей в широком
смысле, иначе не убывающей, если при
называется возрастающей в широком
смысле, иначе не убывающей, если при
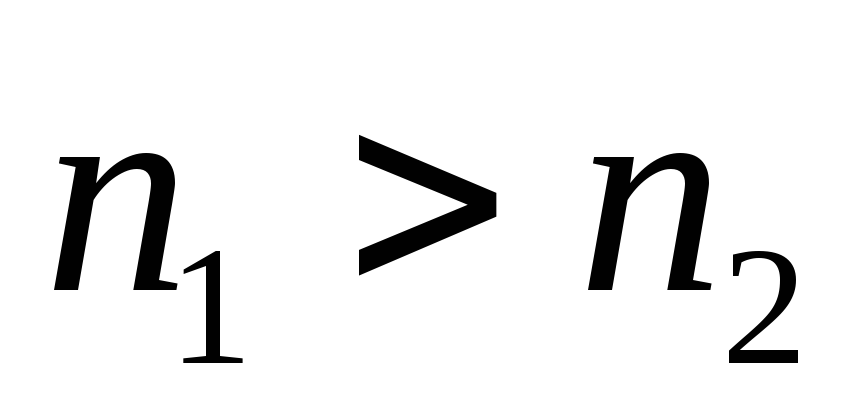 следует
следует
 .
.Переменная
 называется возрастающей в широком
смысле, иначе не убывающей, если при
называется возрастающей в широком
смысле, иначе не убывающей, если при
 следует
следует
 .
.Все перечисленные переменные
 называются монотонными переменными.
Они могут быть строго монотонными и не
строго монотонными.
называются монотонными переменными.
Они могут быть строго монотонными и не
строго монотонными.
ТЕОРЕМА:
Если переменная
 возрастает в узком или широком смысле
и ограничена с верху (означает, что её
значения ограничены с верху), то она
имеет конечный предел.
возрастает в узком или широком смысле
и ограничена с верху (означает, что её
значения ограничены с верху), то она
имеет конечный предел.Если переменная
 убывает в узком или широком смысле и
ограничена снизу (её значения ограничены
снизу), то она имеет конечный предел.
убывает в узком или широком смысле и
ограничена снизу (её значения ограничены
снизу), то она имеет конечный предел.

![]()
![]()
![]()
Можно доказать, что переменная
![]() строго возрастает и ограничена сверху
числом 3. По теореме о существовании
предела и ограниченной монотонной
переменной можно утверждать, что
рассматриваемая переменная
строго возрастает и ограничена сверху
числом 3. По теореме о существовании
предела и ограниченной монотонной
переменной можно утверждать, что
рассматриваемая переменная
![]() имеет предел:
имеет предел:
![]()
В дальнейшем будет выведена формула, позволяющая вычислить этот предел с любой степенью точности
![]()
Число
![]() лежит в основании так называемых
натуральных логарифмов.
лежит в основании так называемых
натуральных логарифмов.
![]()
![]()
![]()
![]() – модуль перехода.
– модуль перехода.
С числом
![]() связано несколько функций, рассмотренных
в математике.
связано несколько функций, рассмотренных
в математике.

Гиперболические функции:
1. ![]() – синус гиперболический.
– синус гиперболический.
2. ![]() – косинус гиперболический.
– косинус гиперболический.
3. ![]() – тангенс гиперболический.
– тангенс гиперболический.
4. ![]() – котангенс гиперболический.
– котангенс гиперболический.
–1

Свойство этих функций:
![]() – нечетные функции,
– нечетные функции,
![]() – четная функция.
– четная функция.
![]() – имеют горизонтальные асимптоты на«+»и на« – » бесконечности.
– имеют горизонтальные асимптоты на«+»и на« – » бесконечности.
![]() – имеет вертикальную асимптоту.
– имеет вертикальную асимптоту.
