
Лекции по матану от множеств до функций / Лекции_1_2
.doc
![]() – бесконечно
малые.
– бесконечно
малые.
![]()
![]()
Этот предел отношения может быть различным в зависимости от быстроты стремления бесконечно малой к нулю.
Определения:
-
Если
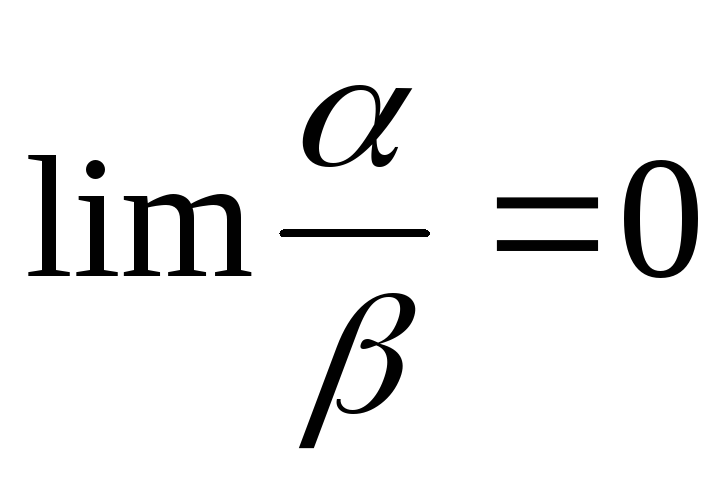 ,
то
,
то
 – бесконечно малое высшего порядка,
чем
– бесконечно малое высшего порядка,
чем
 (по опр.).
(по опр.). -
Если
 ,
то
,
то
 – бесконечно малое низшего порядка,
чем
– бесконечно малое низшего порядка,
чем
 .
. -
Если
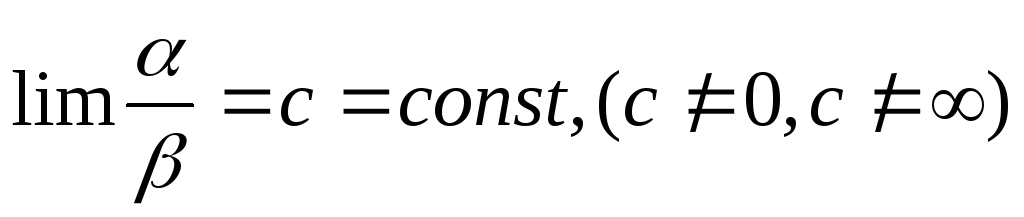 ,
то
,
то
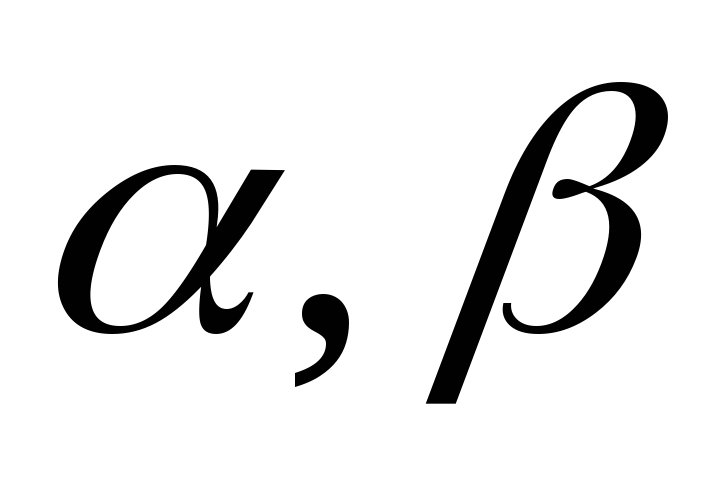 – бесконечно малые одного порядка
малой степени.
– бесконечно малые одного порядка
малой степени. -
Если
 , то
, то
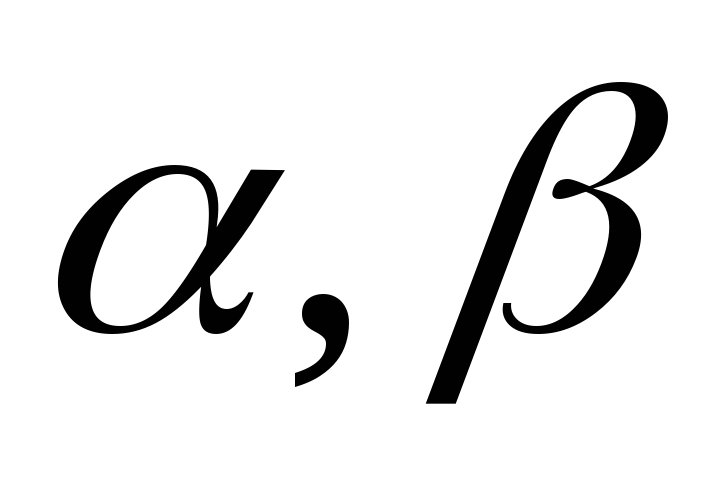 – называются эквивалентными бесконечно
малыми величинами.
Запись:
– называются эквивалентными бесконечно
малыми величинами.
Запись:
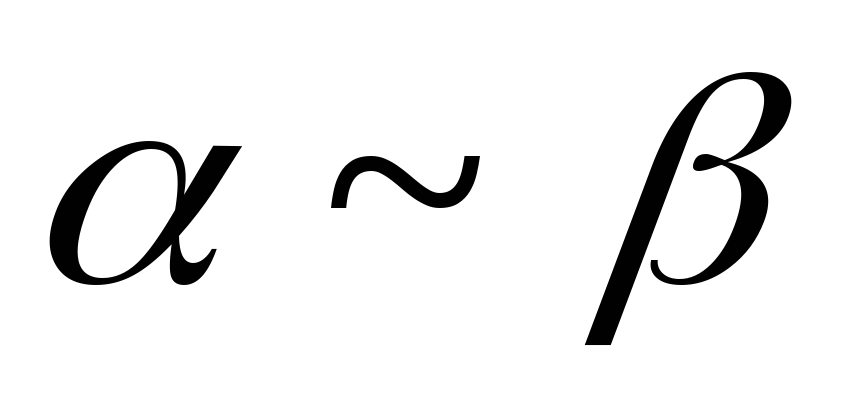 ~
– эквивалентно
~
– эквивалентно
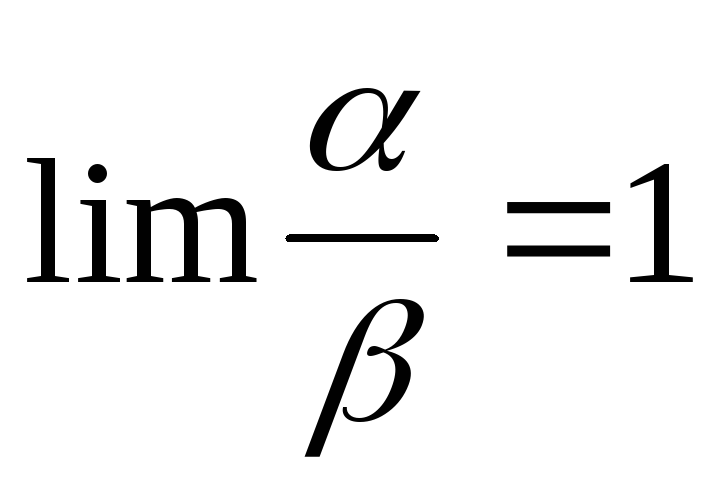 .
. -
Если
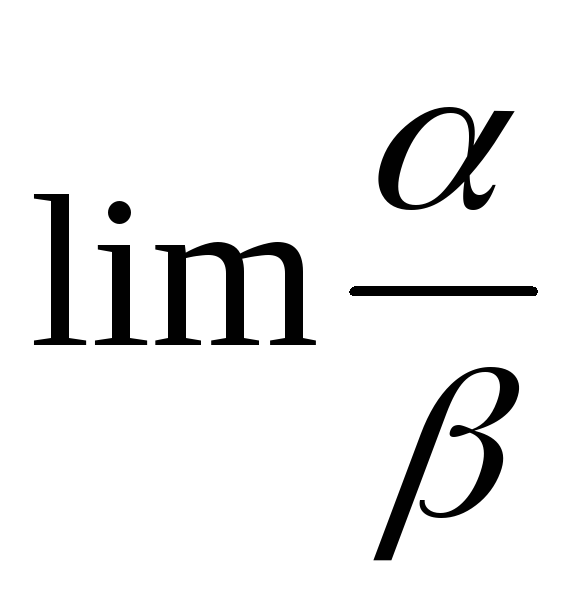 не существует, то
не существует, то
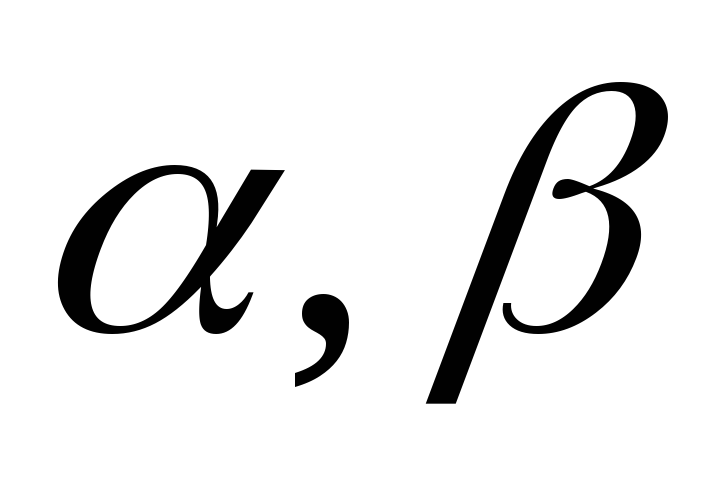 – не сравнимо малые величины.
– не сравнимо малые величины.Примеры:
1.
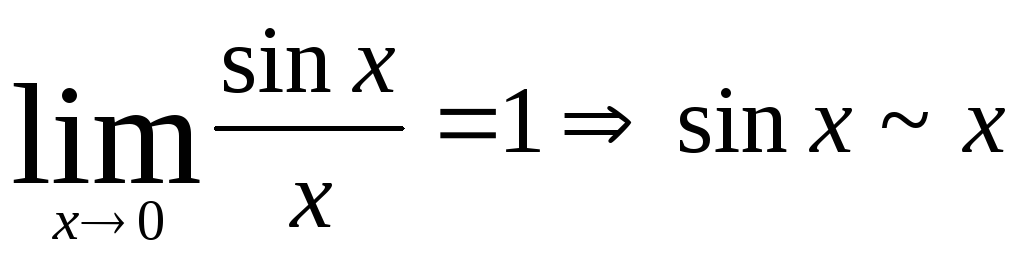 .
.2.
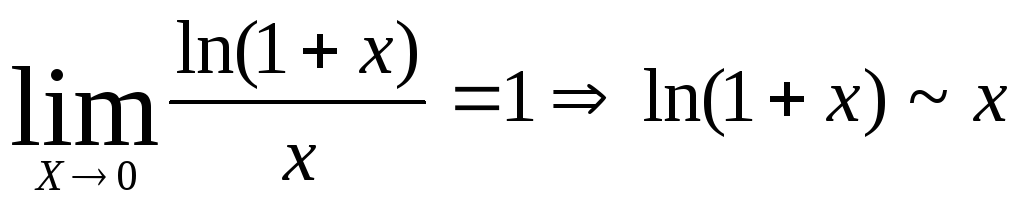 .
.3.
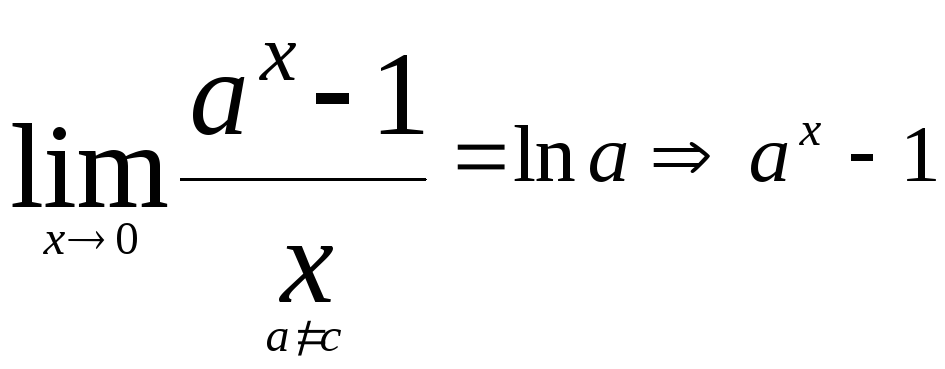 и
и
 – одного порядка …
– одного порядка …4.
 – бесконечно малое высшего порядка
чем
– бесконечно малое высшего порядка
чем
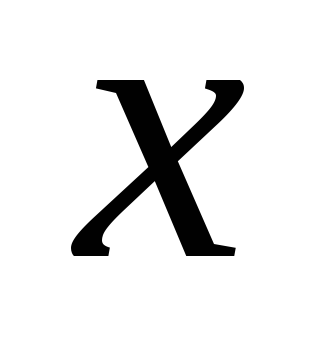 .
.5.
 .
.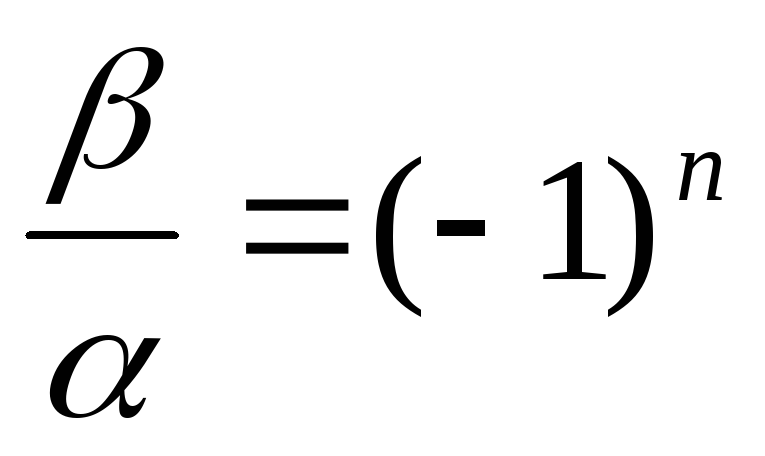 , не имеет предела
при
, не имеет предела
при
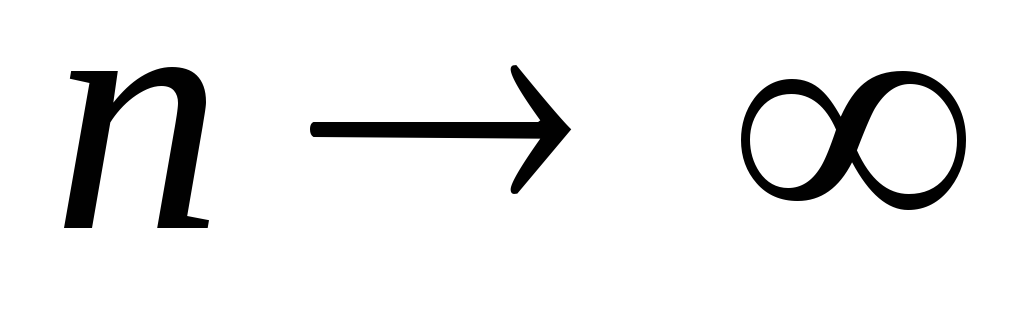 .
. – не сравнимые
бесконечно малые величины.
– не сравнимые
бесконечно малые величины.Часто удобно одну из бесконечно малых взять за основную и с ней сравнивать все остальные бесконечно малые
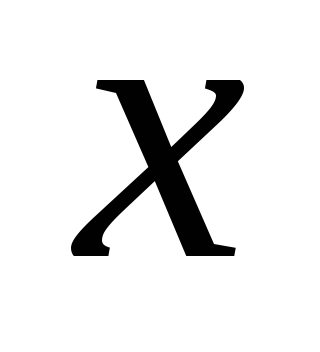 или
или
 – часто означают переменные.
– часто означают переменные.Опр. 6 Бесконечно малое
 , называется низшего порядка по отношению
к бесконечно малому
, называется низшего порядка по отношению
к бесконечно малому
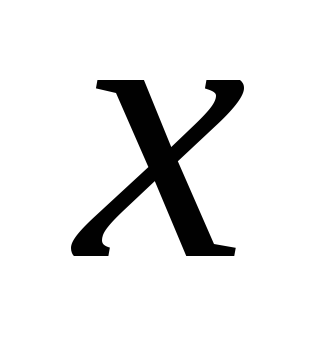 ,
если
,
если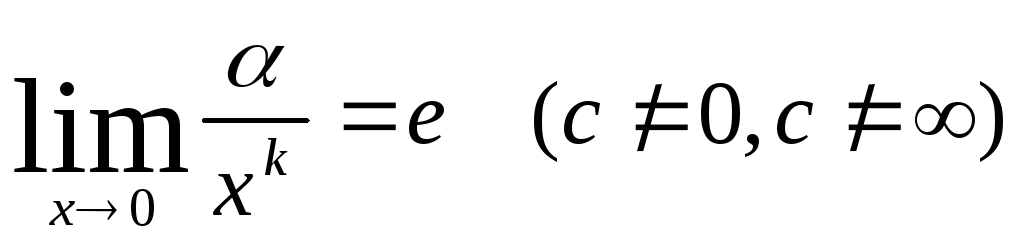 .
.Пример:
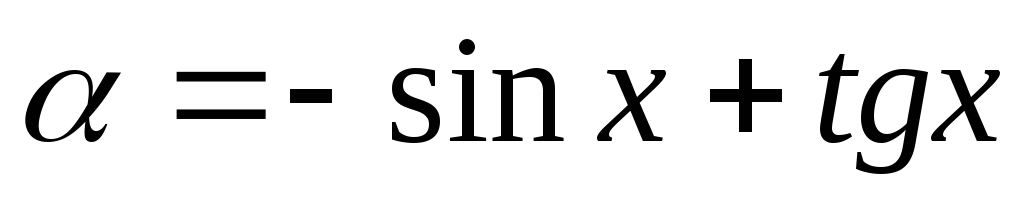 ;
бесконечно малое –
;
бесконечно малое –
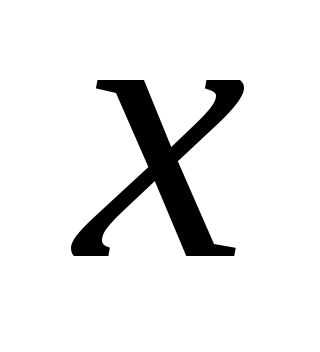 .
1.
.
1. 
 –
высшего порядка,
чем
–
высшего порядка,
чем
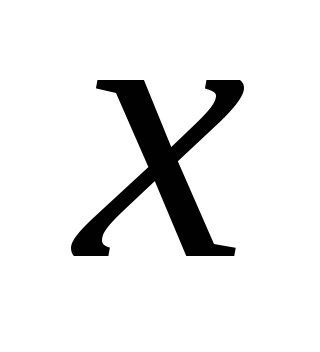 .
.Какого же порядка ??? 2.
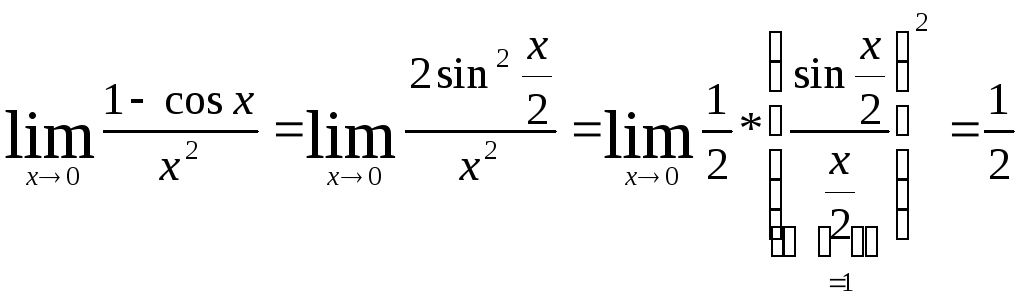 .
.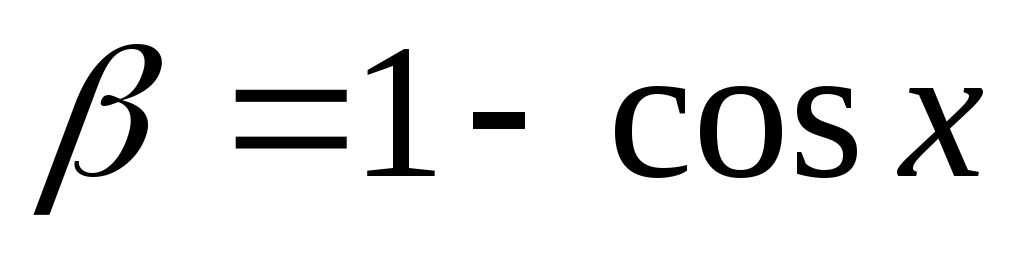 – имеет 2-й порядок
по отношению к
– имеет 2-й порядок
по отношению к
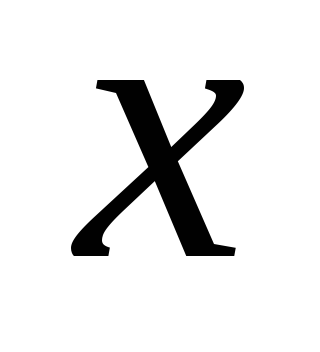 .
3.
.
3.  .
.Следовательно бесконечно малое –
 ,
имеет 3-й порядок малости по отношению
к
,
имеет 3-й порядок малости по отношению
к
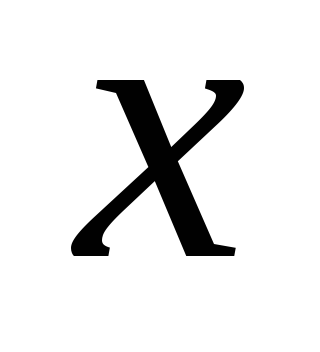 .
.ТЕОРЕМА 1:
Для того чтобы бесконечно малые –
 и
и
 были эквивалентными, необходимо и
достаточно, чтобы разность между ними
была бесконечно малой высшего порядка,
чем каждая из них в отдельности.
были эквивалентными, необходимо и
достаточно, чтобы разность между ними
была бесконечно малой высшего порядка,
чем каждая из них в отдельности.Доказательство:
Необходимость:
Дано:

Требуется доказать:
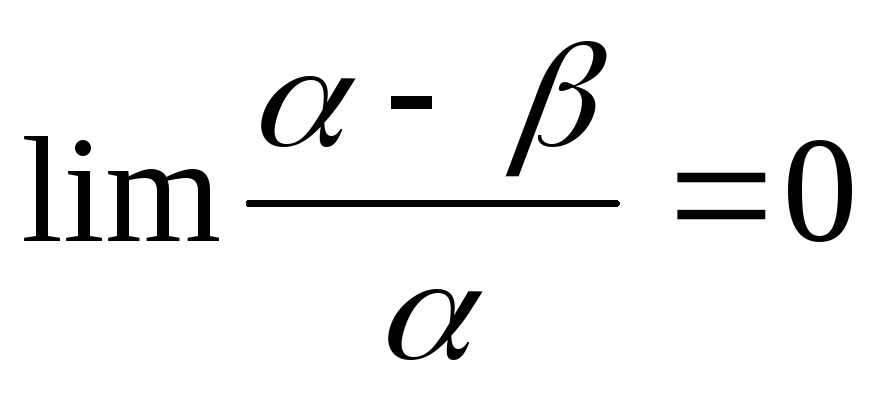
 ч.т.д.
ч.т.д.Достаточность:
Дано:
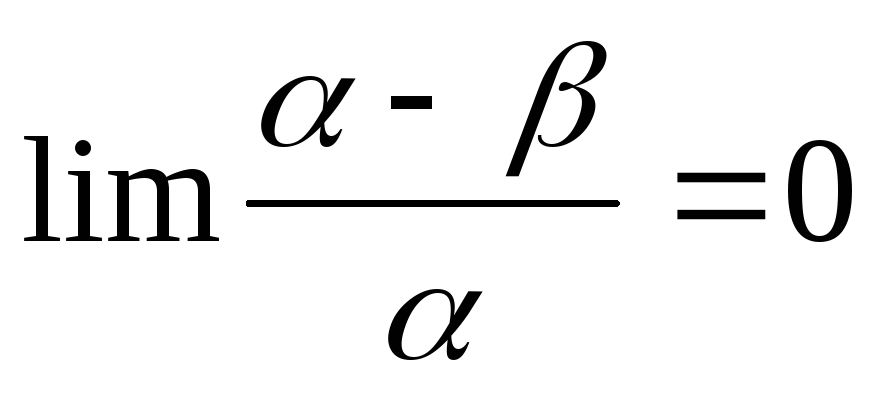
Требуется доказать:

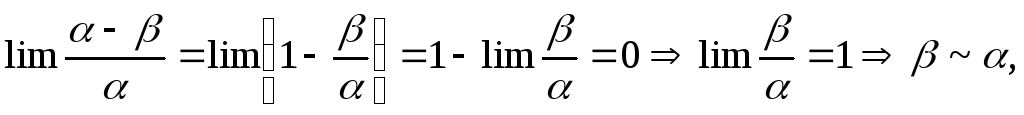 ч.т.д.
ч.т.д.1)

2)
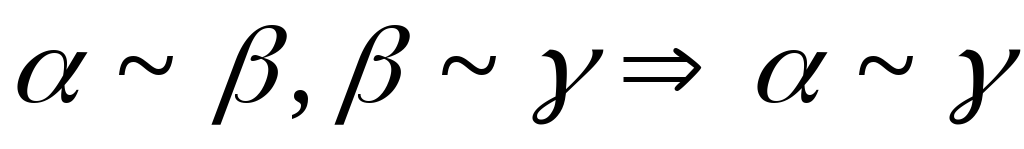
ТЕОРЕМА 2:
При вычислении предела отношений или производной
 бесконечно малого, каждую
из них можно заменить эквивалентной.
бесконечно малого, каждую
из них можно заменить эквивалентной.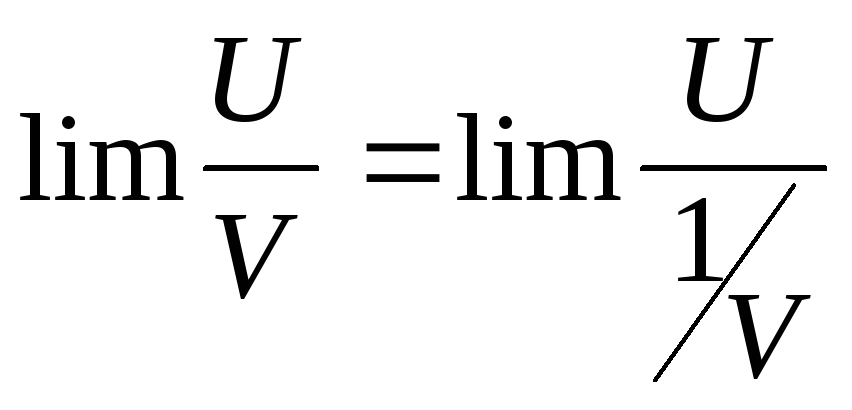
Пусть:
 ,
тогда
,
тогда
 .
.Доказательство:
Рассмотрим
 ,
ч.т.д.
,
ч.т.д.Пример:
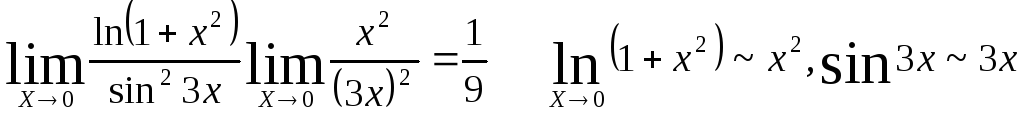
Таблица эквивалентных бесконечно малых:
1.
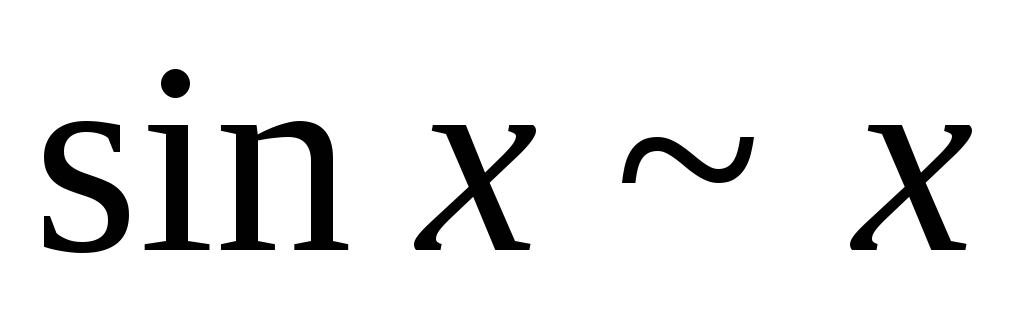
2.
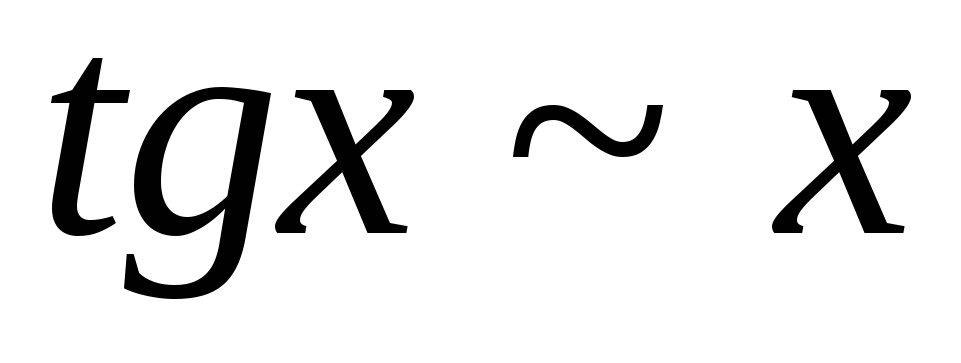
3.
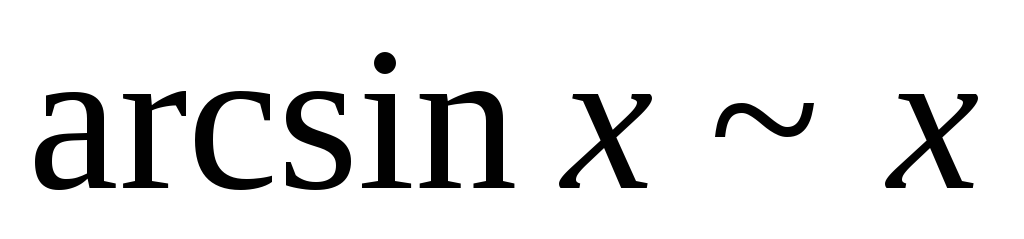
4.

5.
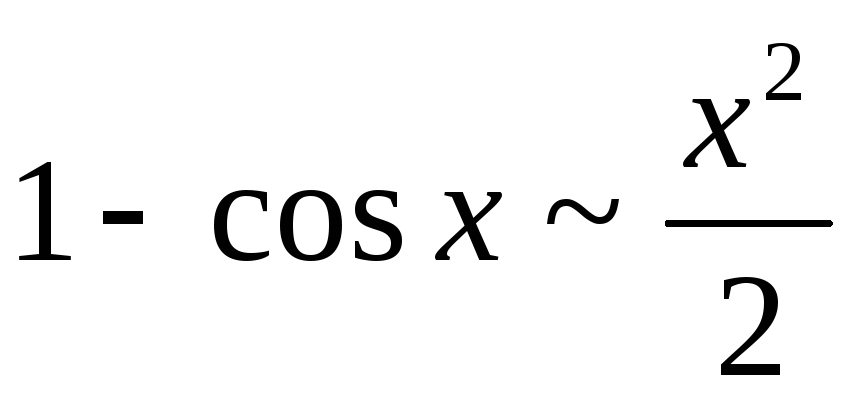
6.

7.

8.
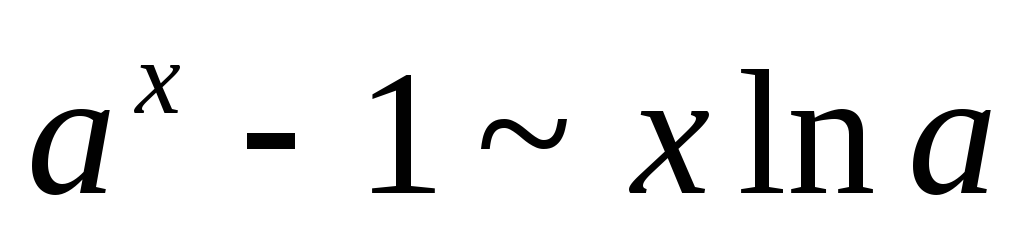
9.
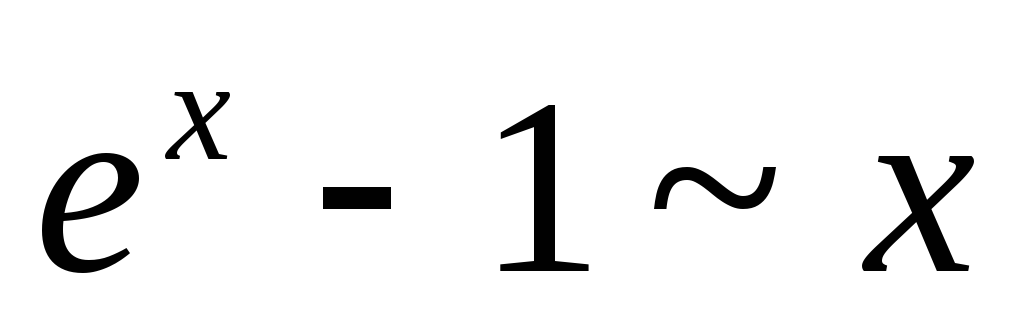
10.

11.

12.

Обобщение теоремы 2
Опр. 7: Две функции
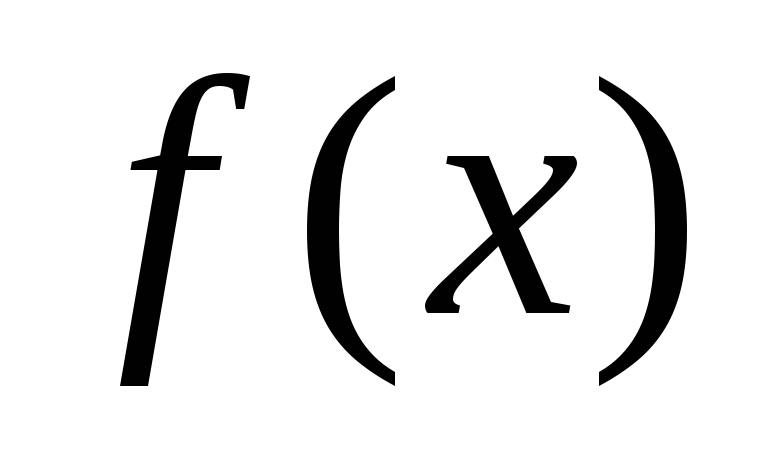 и
и
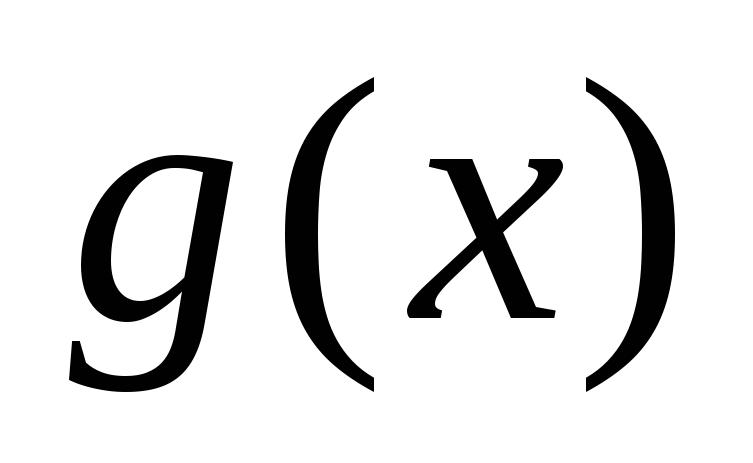 ,
называются эквивалентными при
,
называются эквивалентными при
 ,
если
,
если
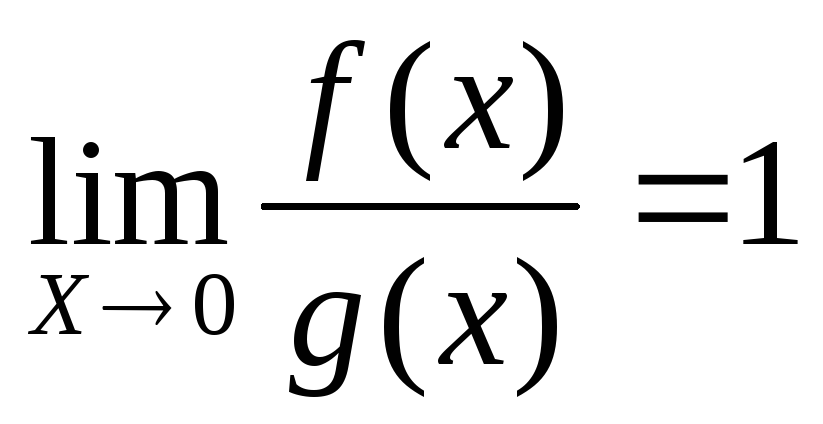
Запись та же самая:
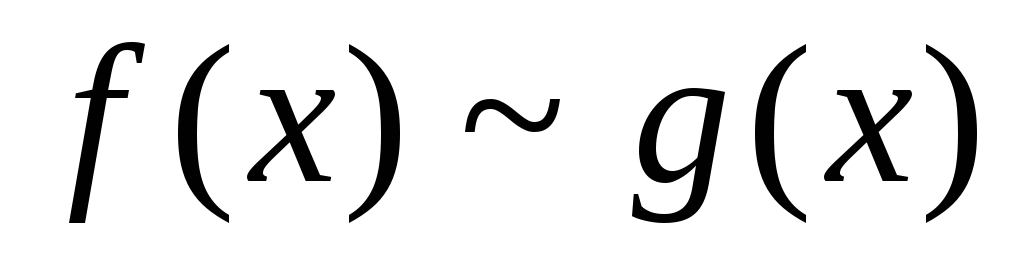
Теорема 2 о эквивалентных бесконечно малых распространяется на случай любых эквивалентных функций.
Формулировка: Если
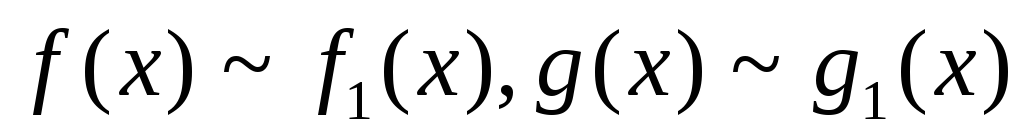 при
при
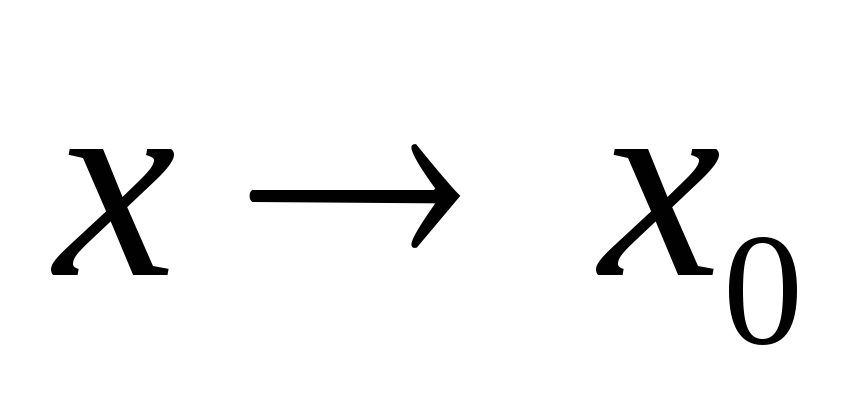 ,
то:
,
то: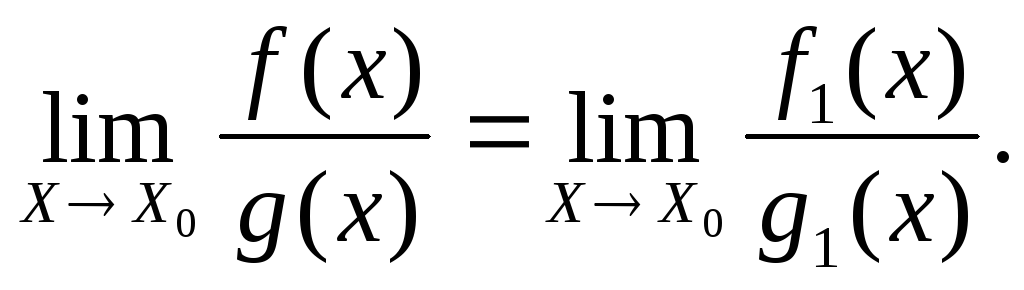
С помощью таблицы эквивалентных бесконечно малых раскрываются различные виды неопределенностей:
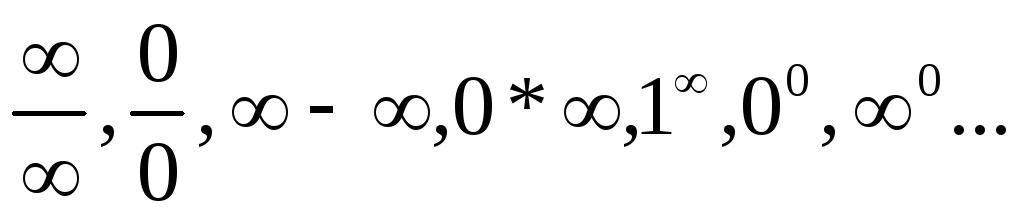
1.
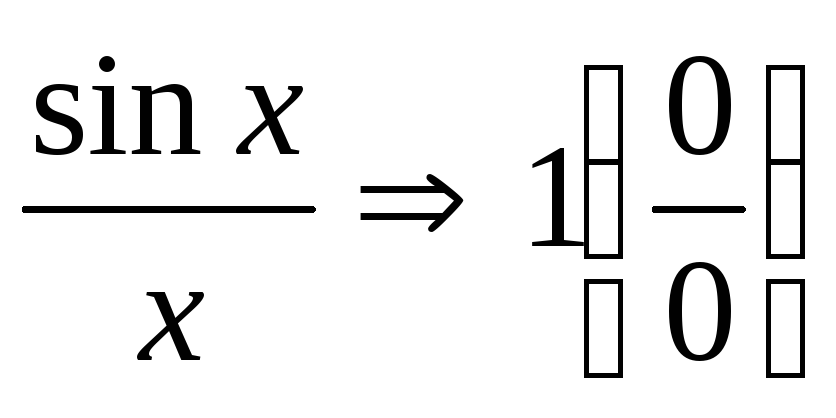
2.
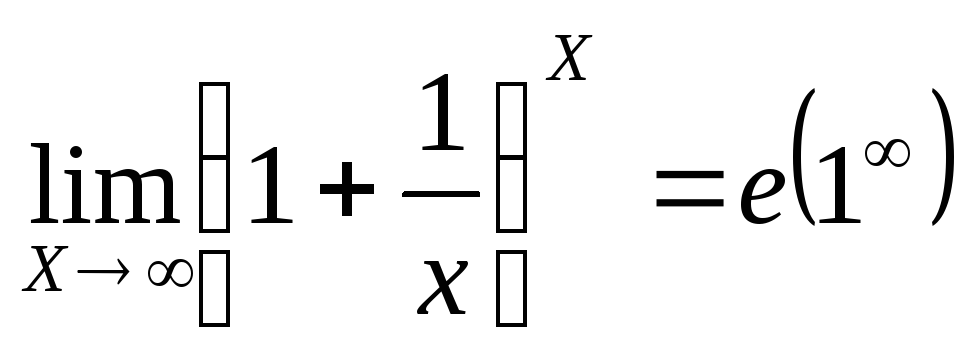
3.
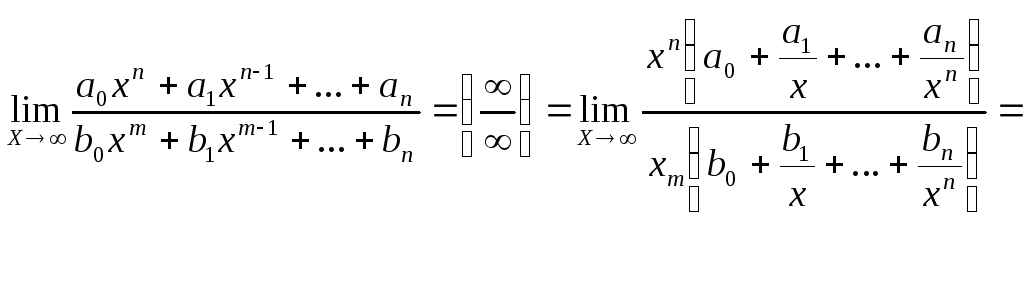
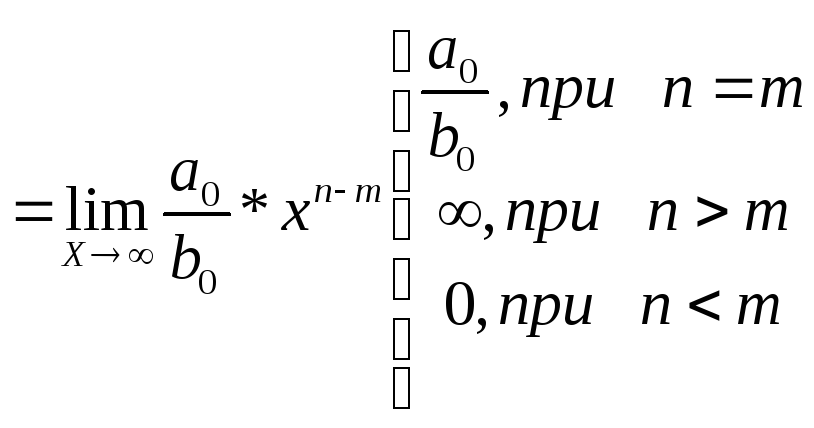
Опр. 8: Если бесконечно малая
 имеет более высокий порядок, чем
бесконечно малая
имеет более высокий порядок, чем
бесконечно малая
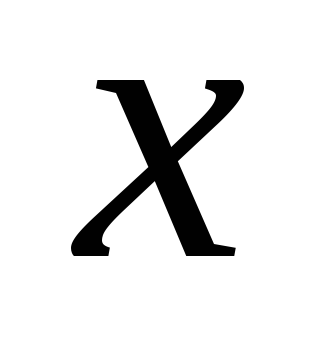 ,
то принимается запись:
,
то принимается запись:
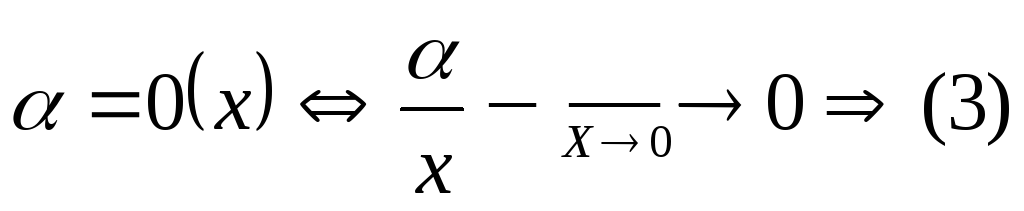 .
.Формулы для
 :
:1.
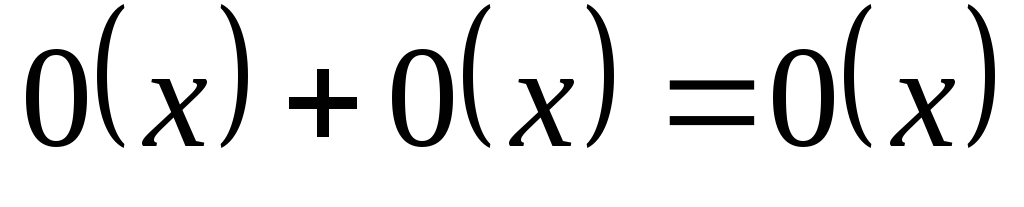
2.
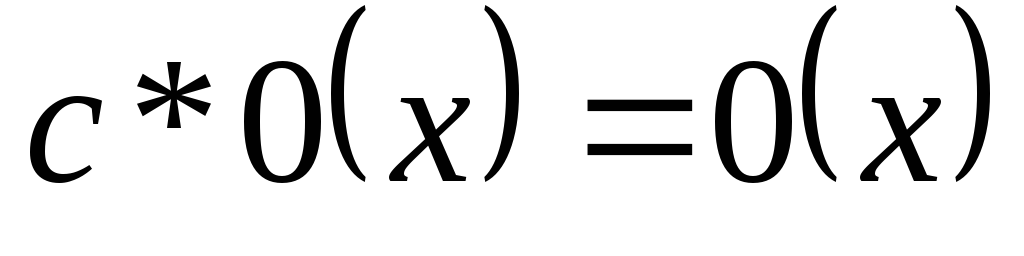
3.

4.

5.
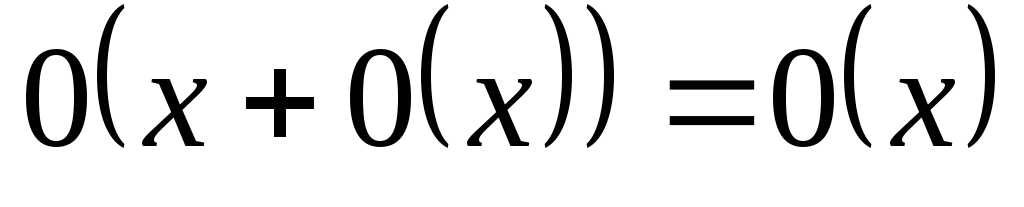
Опр. 8: Если
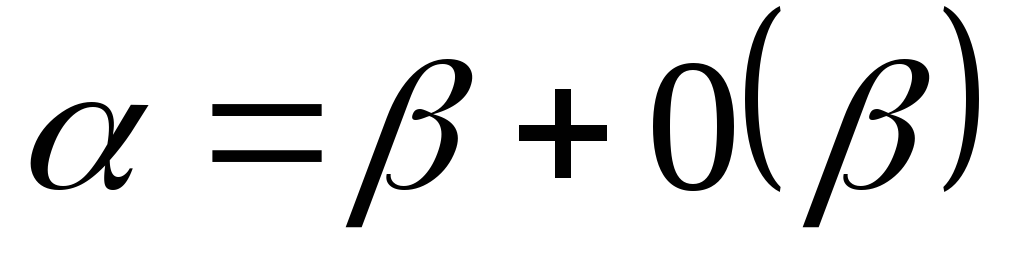 ,
то бесконечно малая
,
то бесконечно малая
 называется главной частью бесконечно
малого
называется главной частью бесконечно
малого
 .
Т. к.
.
Т. к.
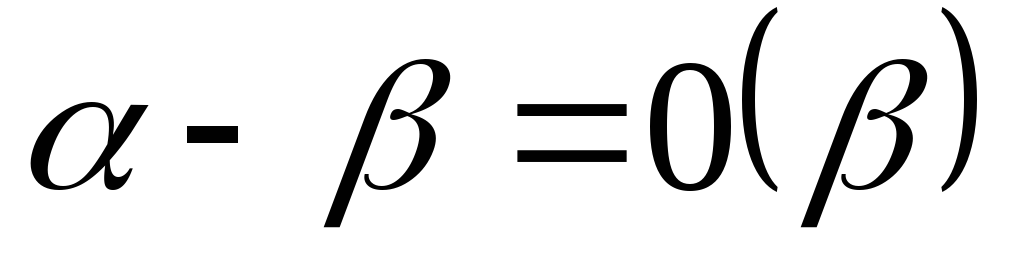 ,
поэтому
,
поэтому
 .
Каждая из двух этих бесконечно малых
является главной частью другой.
.
Каждая из двух этих бесконечно малых
является главной частью другой.Если выполняется
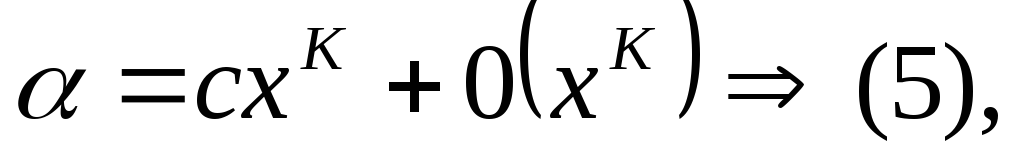 то
то
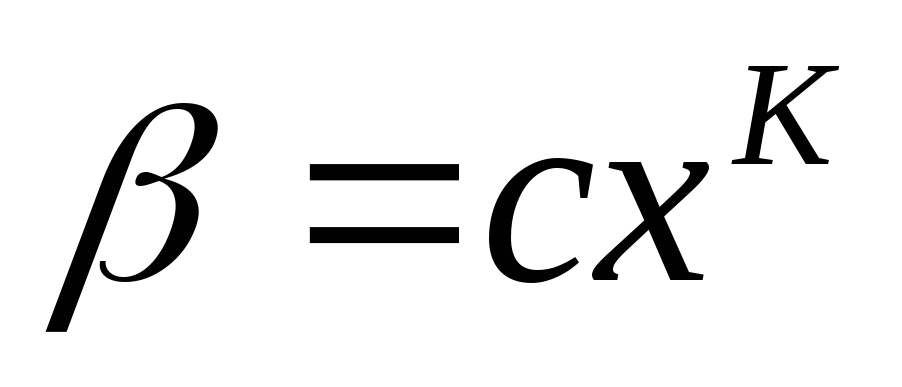 – главная часть
– главная часть
 .
.Таблица эквивалентных бесконечно малых может быть записана в другой форме с использованием символа порядка.
Формула типа
 называется
асимптот. формулой.
называется
асимптот. формулой.Таблица асимптот. Формул:
1.
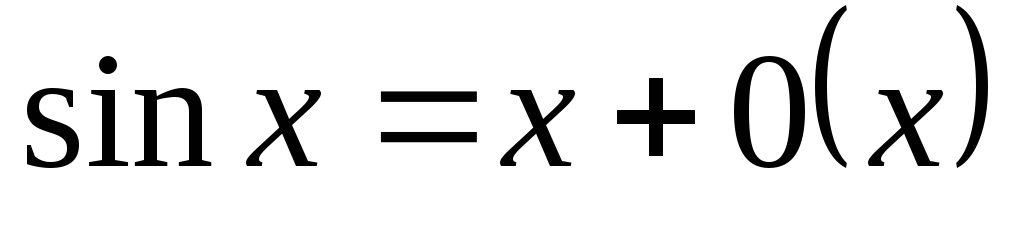
2.
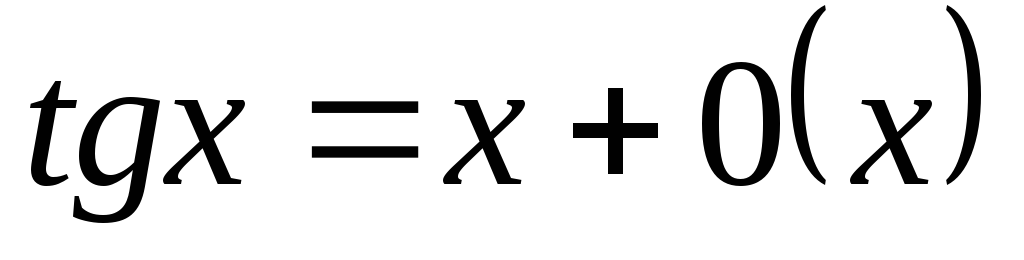
3.

4.

5.
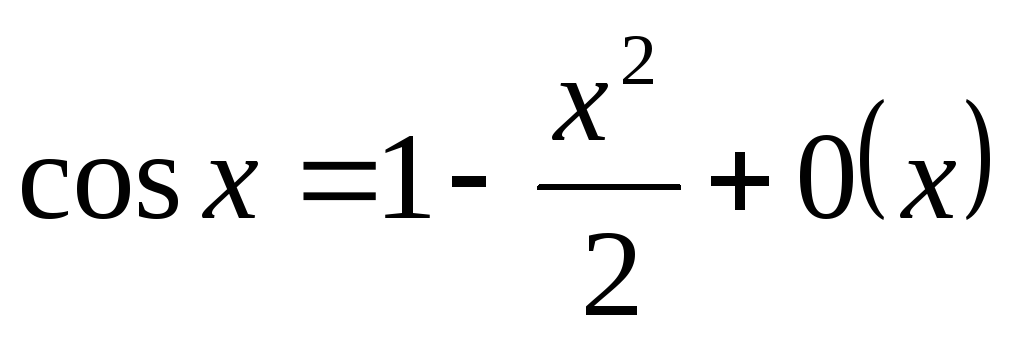
6.
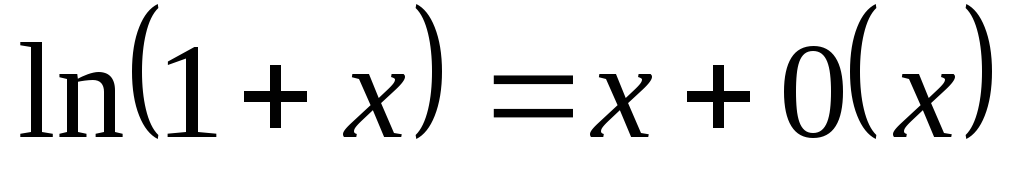
7.

8.

9.
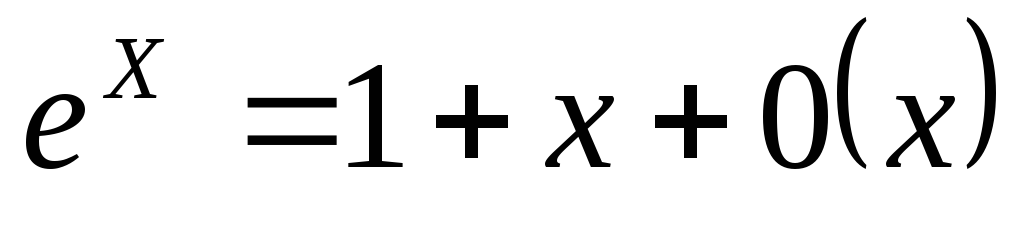
10.
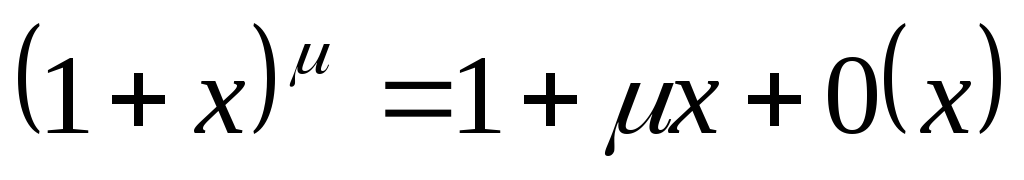
11.
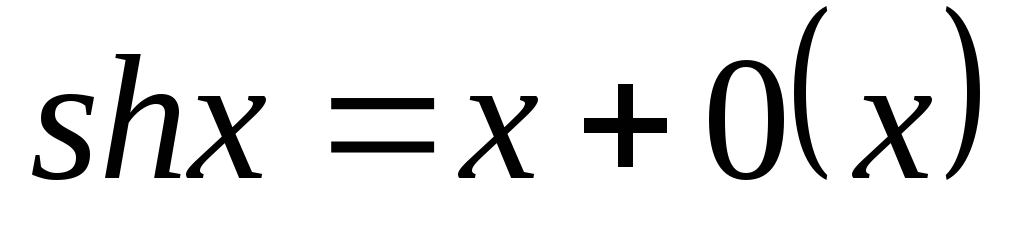
12.
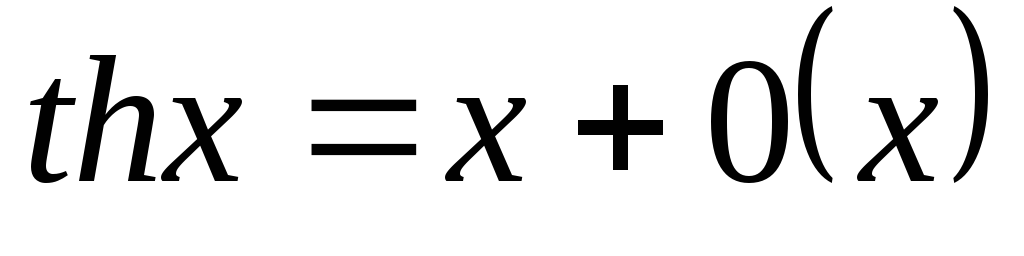
Тезисы:
-
Аналогично сравнению бесконечно малых происходит сравнение бесконечно больших.
-
Сумма бесконечно малых эквивалентна бесконечно малому наинизшего порядка.
 – бесконечно
малая величина.
– бесконечно
малая величина.
Следовательно:
 .
.-
Сумма бесконечно больших эквивалентна бесконечно большому наивысшего порядка роста.
 – бесконечно
большая величина.
– бесконечно
большая величина.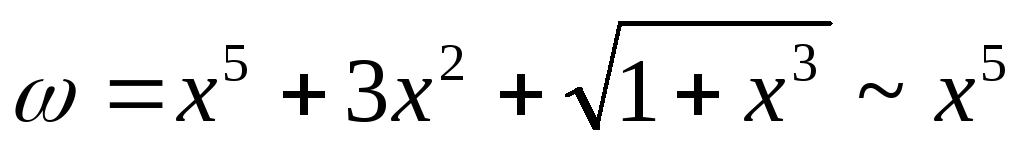
Типовые задачи по вычислению пределов.
-
При вычислении предела отношения и производной бесконечно малой следует пользоваться таблицей бесконечно малых. Каждую бесконечно малую заменяем более простой эквивалентной бесконечно малой…
-
При вычислении предела с бесконечно малой, в которой встречаются сумма и разность, следует пользоваться таблицей асимптотических формул.
-
При раскрытии неопределённости показателя
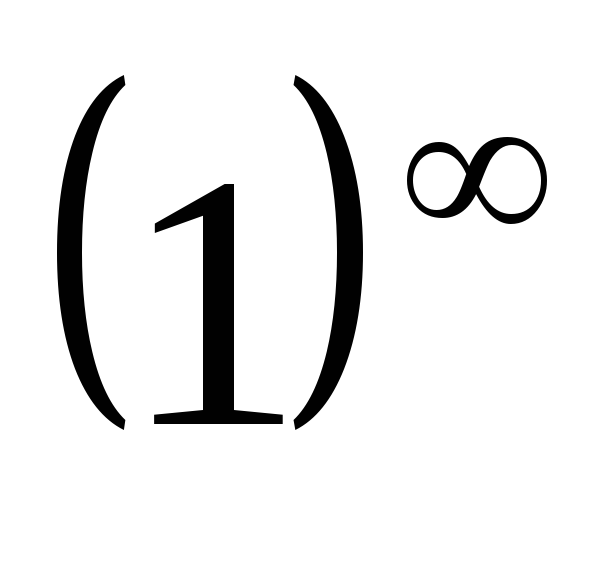 всегда следует прологарифмировать
показательное выражение.
всегда следует прологарифмировать
показательное выражение.
-
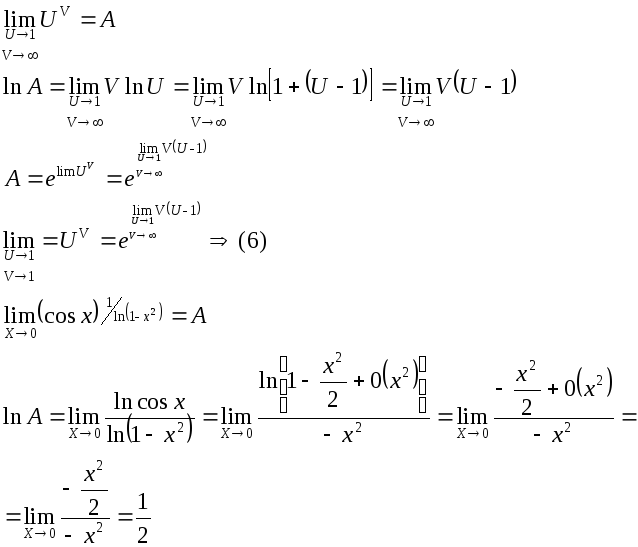
ГЛАВА 2: __________________________________________.
ПАРАГРАФ 1: НЕПРЕРЫВНОСТЬ ФУНКЦИИ.
Понятие о непрерывности функции описывает непрерывные процессы в округе… Непрерывные функции описывают непрерывные процессы.
Будем
обозначать:
![]() – приращение
аргумента.
– приращение
аргумента.
![]() – приращение
функции.
– приращение
функции.
Опр.
1: Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если она определена в окрестности точки
,
если она определена в окрестности точки
![]() и бесконечно малое приращение аргумента
соответствует бесконечно малому
приращению функции
и бесконечно малое приращение аргумента
соответствует бесконечно малому
приращению функции
Под
окрестностью точки понимают любую
![]() – окрестность этой точки.
– окрестность этой точки.
![]()
Запишем
![]() на языке
на языке
![]() – окрестностей,
используя определение предела функции.
– окрестностей,
используя определение предела функции.
Опр.
2: Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если она определена в окрестности точки
,
если она определена в окрестности точки
![]() и по любому
и по любому
![]() можно указать
можно указать
![]() ,
то при выполнении:
,
то при выполнении:
![]() следует:
следует:
![]()
![]()
Запишем
формулу
![]() ещё в другом виде:
ещё в другом виде:
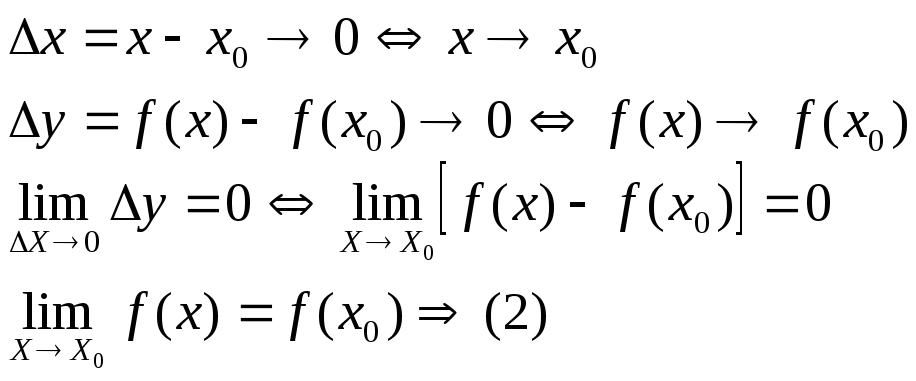
![]() позволяет
сформулировать следующее определение,
равносильное предыдущему.
позволяет
сформулировать следующее определение,
равносильное предыдущему.
Опр.
3: Функция
![]() называется
непрерывной в точке
называется
непрерывной в точке
![]() ,
если она определена в окрестности точки
,
если она определена в окрестности точки
![]() и предел функции равен функции предельного
значения аргумента.
и предел функции равен функции предельного
значения аргумента.
![]()
Для
непрерывной функции знаки предела и
функции можно поменять местами.
Запишем уравнение
![]() ,
употребляя пределы с лева и с права.
Заметим, что если существует двусторонний
предел, то существует оба односторонних
предела и
они равны между
собой, поэтому
,
употребляя пределы с лева и с права.
Заметим, что если существует двусторонний
предел, то существует оба односторонних
предела и
они равны между
собой, поэтому
![]() может быть записана в следующей
эквивалентной форме:
может быть записана в следующей
эквивалентной форме:
![]()
Опр.
4:Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если она определена в окрестности точки
,
если она определена в окрестности точки
![]() ,
существуют конечные пределы с лева и с
права и выполняется равенство:
,
существуют конечные пределы с лева и с
права и выполняется равенство:
![]() .
.
Пределы с лева и справа равны между собой и равны значению функции в точке.
Опр.
5: Функция
![]() называется непрерывной на промежутке,
если она непрерывна в каждой точке
промежутка.
называется непрерывной на промежутке,
если она непрерывна в каждой точке
промежутка.
ПАРАГРАФ 2: ТОЧКИ РАЗРЫВА ФУНКЦИИ.
Опр.
1: Точка
![]() называется точкой разрыва функции
называется точкой разрыва функции
![]() ,
если нарушается хотя бы одно из условий
определения непрерывности функции;
используем опр.
4:
,
если нарушается хотя бы одно из условий
определения непрерывности функции;
используем опр.
4:
Нарушение: – Условие:
1. ![]()
![]() Функция определена
в точках, где
Функция определена
в точках, где
![]() обращается в ноль.
обращается в ноль.
![]()
Эта функция разрывна во всех точках области определения функции, т. к. эти точки изолированы без окрестности.
2. Если пределы с лева и с права не являются конечными
