7. Общие методические рекомендации для решения задач

Итак, чтобы решить задачи настоящего пособия необходимо:

а) четко уяснить, что требуется в задаче;

б) определить для конкретной задачи систему координат, переменные в которых решение задачи наиболее рационально, составить неравенства, определяющие область интегрирования;

в) определить порядок, пределы интегрирования;

Замечание: Если возникают затруднения в выборе порядка интегрирования и пределов интегрирования, необходимо определяющие неравенства дополнить чертежом и рисунком.

г) записать двойные или тройные интегралы, с помощью которых вычисляются искомые величины;

д) осуществить переход от одной системы координат к другой, если это необходимо, и вычислить якобиан. К большинству задач, приведенных в пособии, даны рекомендации по использованию удобной системы координат.

е) в новой системе координат также определить порядок интегрирования соответствующими неравенствами.

ж) вычислить интегралы и оформить надлежащим образом решение задачи.

Для закрепления теоретических знаний и получения практических навыков при вычислении кратных интегралов, а также четкого представления применения кратных интегралов в приложениях и практических задачах рекомендуется самостоятельно выполнить все задачи одного из вариантов.

8. Задачи (25 вариантов)

9. Задачи (25 вариантов) приведены на стр. 18-42 .

Литература:

1. Архипов Г.И., Садовничий В.А., Чубариков В.И. Лекции по математическому анализу. М., «Выс. шк.», 2000, 695 с.

2. Берман Г.Н. Сборник задач по курсу математического анализа. М., Наука, 1964, 444 с.

3. Бохан К.А., Егорова И.А., Лащёнов К.В. Курс математического анализа, том II, М.. «Просвещение», 1966., 380 с.

4. Виноградова И.А., Олехник С.Н., Садовничий В.А., Задачи и упражнения по математическому анализу. Т. I, М., «Выс. шк.», 2002, 725 с.

5. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике, т.П,Физматгиз,1958, 286 с.

6. Давыдов Н.А., Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу, М., 1964, 198 с.

7. Минорский Н.П. Сборник задач по высшей математике. М., «Наука», 1978, 352 с.

В А Р И А Н Т 1

1.1. Определить пределы интегрирования в интеграле гдеS-круг если выполнить интегрирование сначала поx, а потом по y.

1.2. Вводя полярные координаты, вычислить площадь, ограниченную следующей кривой

1.3. Найти площадь, ограниченную кривыми x+y=a, x+y=b, ,

1.4. Найти объём, ограниченный следующими поверхностями x+y+2=6; x=0; z=0; x+2y=4.

1.5. Найти объём, ограниченный поверхностью x>0, y>0, z>0.

1.6. Найти длину поверхности приz>0, 0<x<a; 0<y<b.

1.7. Найти координаты центра тяжести однородной пластины (правая петля).

1.8. Найти объём, ограниченный поверхностью

1.9. Найти координаты центра тяжести однородного тела, ограниченного следующей поверхностью x>0, y>0, z>0.

1.10. Найти момент инерции относительно оси OZ тела, ограниченного следующими поверхностями: x<0, x=a, y=0, y=b, z=0, z=c.

В А Р И А Н Т 2

2.1. Определить пределы интегрирования в интеграле для площадиS, ограниченной прямыми x=0, y=0, x+y=a.

2.2. Вводя полярные координаты, вычислить площадь, ограниченную следующей кривой

2.3. Найти площадь, ограниченную кривыми y=m, y=n; a<b, m<n.

2.4. Найти объём, ограниченный следующими поверхностями x-y+z=6; x+y=2, x=y; y=0, z=0.

2.5. Найти объём, ограниченный поверхностью x>0, y>0, z>0.

2.6. Найти длину поверхности при0<x<a.

2.7. Найти координаты центра тяжести поверхности сегмента шара приh<z<a.

2.8. Найти объём ограниченный поверхностью

2.9. Найти координаты центра тяжести однородного тела, ограниченного следующей поверхностью x>0, y>0, z>0.

2.10. Найти момент инерции относительно оси OZ тела, ограниченного следующими поверхностями: z=0, .

В А Р И А Н Т 3

3.1. В интеграле площадьS ограниченна прямыми x=y, y=0, x+y=2. Определить пределы интегрирования, если внутреннее интегрирование совершается по x, а также, если оно совершается по y.

3.2. Вводя полярные координаты, вычислить площадь, ограниченную следующей кривой (лист Декарта) – площадь петли.

3.3. Найти площадь, ограниченную кривыми x>0, y>0.

3.4. Найти объём, ограниченный следующими поверхностями x-y+z=6; x=3, x=y; y=0, z=0.

3.5. Найти объём, ограниченный поверхностью .

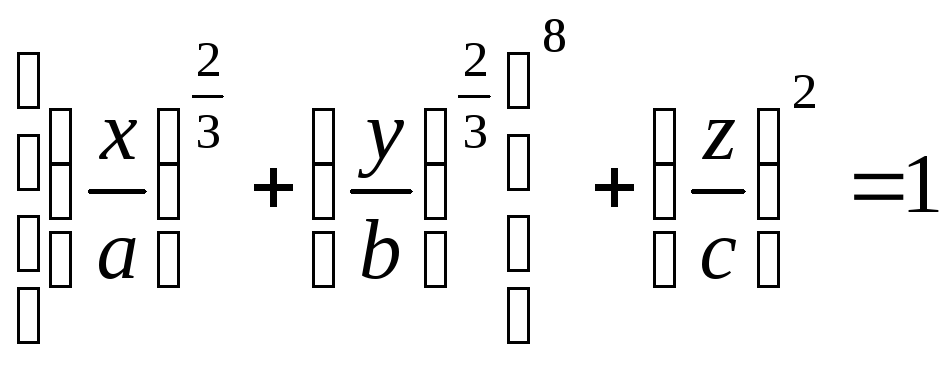3.6. Найти величину поверхности вырезанной поверхностямиx=a.

3.7. Найти координаты центра тяжести поверхности геликоида ,при.

3.8. Найти объём, ограниченный поверхностью

3.9. Найти координаты центра тяжести однородного тела, ограниченного следующей поверхностью ,, z=0.

3.10. Найти момент инерции относительно оси OZ тела, ограниченного следующими поверхностями: 0<z<h.

В А Р И А Н Т 4

4.1. Определить в интеграле пределы интегрирования, если:S – параллелограмм со сторонами y=0, y=a, y=x, y=x-2a.Рассмотреть оба возможных порядка интегрирования.

4.2. Вводя полярные координаты, вычислить площадь, ограниченную следующими кривыми

4.3. Найти площадь, ограниченную кривыми

4.4. Найти объем, ограниченный следующими поверхностями:

4.5. Найти объем, ограниченный поверхностями

4.6. Найти величину поверхности части цилиндра заключенной внутри цилиндра

4.7. Найти координаты центра тяжести поверхности ограниченной плоскостямиx= 0, y=0, x+y=1.

4.8. Найти объем, ограниченный поверхностью

4.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями

4.10. Найти момент инерции относительно оси Oz тела, ограниченного следующими поверхностями

В А Р И А Н Т 5

5.1. Определить в интеграле пределы интегрирования, еслиS – площадь, ограниченная прямыми

5.2. Вводя полярные координаты, вычислить площадь, ограниченную следующими кривыми

5.3. Найти площадь, ограниченную кривыми

5.4. Найти объем, ограниченный следующими поверхностями:

5.5. Найти объем, ограниченный следующими поверхностями:

5.6. Найти величину поверхности части шара , заключенный внутри цилиндра

5.7. Найти координаты центра тяжести поверхности ограниченной поверхностямиy= 0, y=kx, z=0.

5.8. Найти объем, ограниченный поверхностью

5.9. Найти координаты центра тяжести однородного тела, ограниченного следующей поверхностью

5.10. Найти момент инерции относительно оси ОZ, ограниченного следующей поверхностью .

В А Р И А Н Т 6

6.1. Определить в интеграле пределы интегрирования, если:S – область между прямой y=x-2 и параболой (два способа).

6.2. Вводя полярные координаты, вычислить площадь, ограниченную следующей кривой (подэра эллипса).

6.3. Найти площадь, ограниченную кривыми .

6.4. Найти объем, ограниченный следующими поверхностями:

6.5. Найти объем, ограниченный следующими поверхностями:

6.6. Найти величину поверхности части шара , заключенный вне цилиндра(Задача Вивиани).

6.7. Найти координаты центра тяжести части поверхностиограниченной плоскостями

6.8. Найти объем, ограниченный поверхностью

6.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями

6.10. Найти момент инерции относительно оси Oz тела, ограниченного следующей поверхностью

В А Р И А Н Т 7

7.1. Определить в интеграле пределы интегрирования, еслиS-параллелограмм со сторонами (оба способа).

7.2. Вводя полярные координаты, вычислить площадь, ограниченную следующей кривой: (лемниската).

7.3. Найти площадь, ограниченную кривыми .

7.4. Найти объем, ограниченный следующими поверхностями .

7.5. Найти объем, ограниченный поверхностями

7.6. Найти величину поверхности части цилиндров , расположенной внутри шара.

7.7. Найти координаты центра тяжести части поверхности , ограниченной плоскостями:.

7.8. Найти объем, ограниченный поверхностью .

7.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями

7.10. Найти момент инерции относительно оси тела, ограниченного следующими поверхностями:

В А Р И А Н Т 8

8.1. Определить в интегралепределы интегрирования, еслиS определяется так:

8.2. Найти площадь, ограниченную кривой

8.3. Найти площадь, ограниченную кривыми

8.4. Найти объем, ограниченный следующими поверхностями

8.5. Найти объем, ограниченный поверхностью

8.6. Найти величину поверхности части конуса расположенной внутри цилиндра

8.7. Найти моменты инерции поверхности конуса приотносительно оси.

8.8. Найти объем, ограниченной поверхностью

8.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями

8.10. Найти момент инерции относительно оси тела, ограниченного следующей поверхностью

В А Р И А Н Т 9

9.1. Переменить порядок интегрирования в

9.2. Найти площадь, ограниченную кривой

9.3. Найти площадь, ограниченную кривыми

9.4. Найти объем, ограниченной следующими поверхностями

9.5. Найти объем, ограниченной поверхностью

9.6. Найти величину поверхности части конуса вырезанной поверхностью

9.7. Найти момент инерции поверхности однородного шара

относительно диаметра.

9.8. Найти объем, ограниченный поверхностью

9.9. Найти координаты центров тяжести однородного тела, ограниченного следующими поверхностями

9.10. Найти момент инерции тора относительно его оси вращения.

В А Р И А Н Т 10

10.1. Переменить порядок интегрирования в .

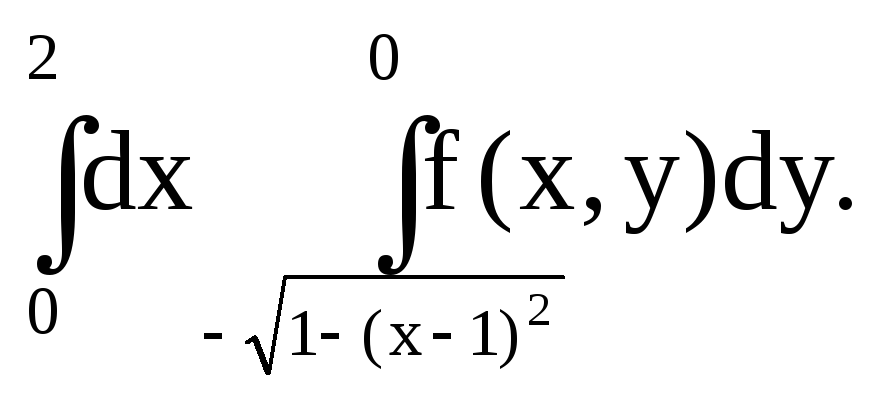10.2. Найти площадь, ограниченную кривой

10.3. Найти площадь, ограниченную эллипсом

10.4. Найти объем, ограниченный следующими поверхностями

10.5. Найти объем, ограниченный следующими поверхностями

10.6. Найти величину части поверхности , проекция которой на плоскостьограничена первым витком спирали Архимедаи осью.

10.7. Найти момент инерции части поверхности параболоида

относительно при

10.8. Найти объем, ограниченный поверхностью

10.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями:

10.10. Найти момент инерции тора относительно его экваториального диаметра.

В А Р И А Н Т 11

11.1. Изменить порядок интегрирования в

11.2. Найти площадь, ограниченную кривой (площадь петли).

11.3. Найти площадь, ограниченную линией

11.4. Найти объем, ограниченный следующими поверхностями

11.5. Найти объем, ограниченный следующими поверхностями

11.6. Найти величину поверхности при условии

11.7. Найти момент инерции части шарового сегментаприотносительно

11.8. Найти объем, ограниченный поверхностью

11.9. Найти координаты центра тяжести однородного тела, ограниченного поверхностью сегмента шара ,.

11.10. Найти момент инерции эллиптического конуса относительно оси

В А Р И А Н Т 12

12.1. Переменить порядок интегрирования в

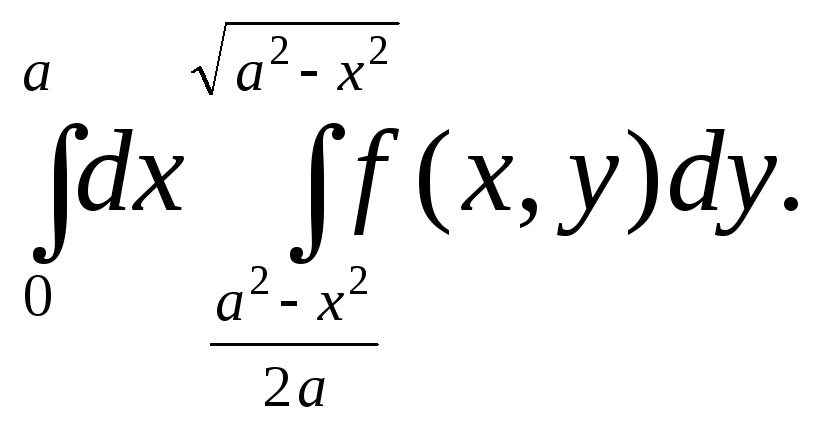
12.2. Найти площадь, ограниченную кривой

12.3. Пользуясь формулой вычислить площадь ограниченную следующими линиями

12.4. Найти объем, ограниченный следующими поверхностями

12.5. Найти объем, ограниченный следующими поверхностями

12.6. Найти величину поверхности внутри цилиндра

12.7. Вычислить двойной интеграл , взятый по поверхности эллипсоида

где - расстояние от центра эллипсоида до плоскости, касательной к элементуds поверхности эллипсоида.

12.8. Найти объем ограниченный поверхностью .

12.9. Найти координаты центра тяжести однородного тела, ограниченного поверхностью

12.10. Найти момент инерции кругового цилиндра высоты H и радиуса основания R-относительно диаметра основания.

В А Р И А Н Т 13

13.1. Переменить порядок интегрирования в .

13.2. Найти площадь, ограниченную кривой

13.3. Вычислить площадь, пользуясь формулой ограниченную следующими кривыми

13.4. Найти объем, ограниченный следующими поверхностями

13.5. Найти объем, ограниченный поверхностями

13.6. Найти величину поверхности внутри цилиндра

13.7. Вычислить интеграл , взятый по поверхности шара, если- расстояние элемента поверхности до точки, расположенной вне шара.

13.8. Найти объем ограниченный поверхностью .

13.9. Найти координаты центров тяжести однородного тела, ограниченного поверхностью

13.10. Найти момент инерции кругового конуса высоты H и радиуса основания R-относительно диаметра основания.

В А Р И А Н Т 14

14.1. Переменить порядок интегрирования 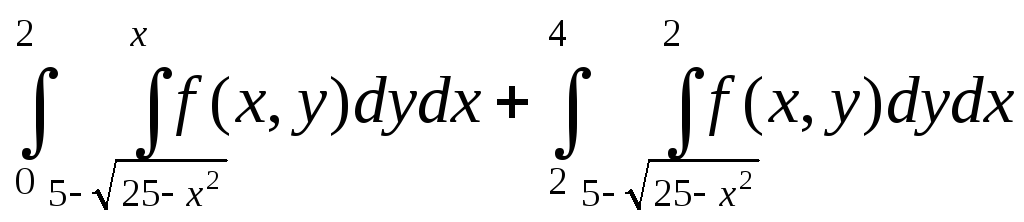и объединить.

14.2. Найти площадь, ограниченную кривой

14.3. Пользуясь формулой вычислить площадь, ограниченную следующими кривыми

14.4. Найти объем, ограниченный следующими поверхностями

14.5. Найти объем, ограниченный поверхностью

14.6. Найти величину поверхности внутри цилиндра

14.7. Показать, что интеграл 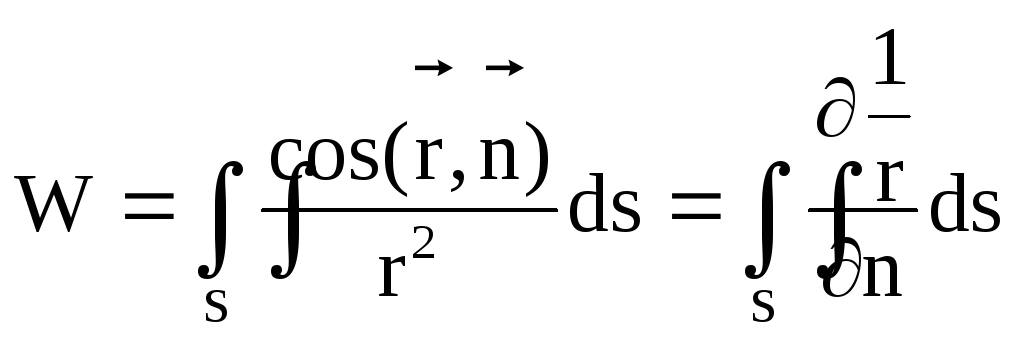, взятый по поверхностиS, равен телесному углу , под которым поверхность S видна из начала координат. Здесь - радиус-вектор из начала координат к элементу поверхности , - нормаль к поверхности, образующей с векторомиз начала острый угол. Величинаравна

14.8. Найти объём, ограниченный поверхностью

14.9. Найти координаты центра тяжести однородного тела, ограниченного поверхностью x=0, y=0, z=0.

14.10. Определить высоту h и радиус основания a однородного цилиндра так, чтобы эллипсоид инерции для этого цилиндра обратился в шар.

В А Р И А Н Т 15

15.1. Переменить порядок интегрирования, а так же перейти к полярным координатам

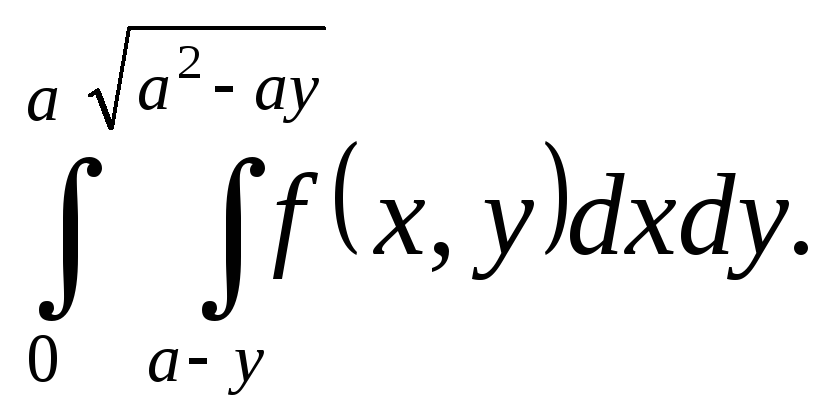
15.2. Найти площадь, ограниченную кривой x>0, y>0.

15.3. Вычислить площадь, ограниченную кривыми

15.4. Найти объём, ограниченный следующими поверхностями

15.5. Найти объём, ограниченный поверхностью

15.6. Найти величину поверхности внутри цилиндрапри.

15.7. Найти координаты центра тяжести, однородного тела, ограниченного следующими поверхностями x+y+z=a, x=0, y=0, z=0.

15.8. Найти объём, ограниченный поверхностью

15.9. Найти координаты центра тяжести однородного тела, ограниченного следующими поверхностями ,x=a, y=b, z=0.

15.10. Доказать, что момент инерции тела относительно осивыражается формулойгде коэффициенты равны соответствующим моментам инерции и центробежным моментамНа каждой прямой, проходящей через центр тяжести тела, отложен отрезок длиной.Доказать, что концы этих отрезков лежат на эллипсоиде. Этот эллипсоид называется эллипсоидом инерции данного тела.

В А Р И А Н Т 16

16.1. Переменить порядок интегрирования, а также перейти к полярным координатам:

16.2. Найти площадь, ограниченную кривой =(площадь петли).

16.3. Вычислить площадь, ограниченную кривыми лемнискатой и окружностью(использовать формулуи перейти к полярным координатам).

16.4. Найти объём, ограниченный поверхностями ,; z>0.

16.5. Найти объём, ограниченный поверхностями cz=xy, +=1,z=0; x>0, y>0.

16.6. Найти величину поверхности , приx>0, y>0, z>0.

16.7. Найти центр тяжести однородного тела, ограниченного поверхностями , x=a, y=b, z=0.

16.8. Найти объём, ограниченный поверхностью=.

16.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле , взятому по объёмуv и заданному следующим образом:

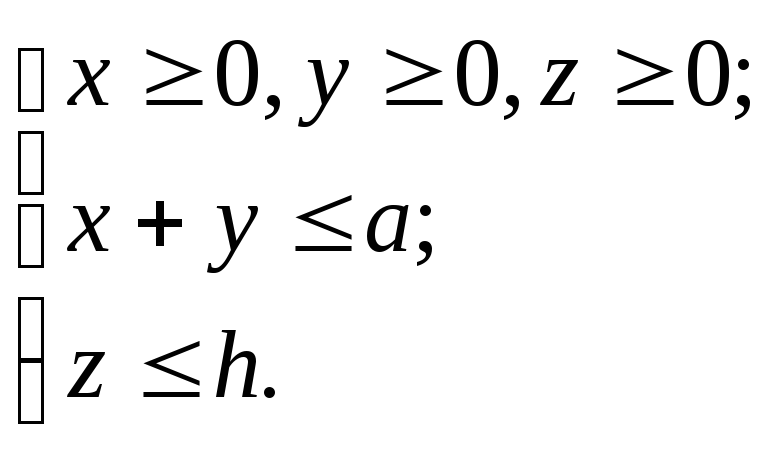
16.10. Определить высоту h и радиус основания a однородного цилиндра так, чтобы эллипсоид инерции для этого цилиндра обратился в конус.

В А Р И А Н Т 17

17.1. Определить пределы интегрирования в двойном интеграле в декартовых и полярных координатах, если определяется так:

17.2. В интегралеобласть интегрирования четверть круга, x>0, y>0. Заменой переменных превратить её в прямоугольник.

17.3. Вычислить площадь, ограниченную кривыми: кардиоидой и окружностью(используя формулуи перейти к полярным координатам.

17.4. Найти объём, ограниченный следующими поверхностями ,x+z =2a.

17.5. Найти объём, ограниченный поверхностями +=2z, +=1,z=0.

17.6. Найти величину поверхности (x+y)²+z=1 при x>0, y>0, z>0.

17.7. Найти объём, ограниченный поверхностью =1; x>0, y>0, z>0 путём введения сферических обобщенных координат (Примечание. ЯкобианJ=abc )

17.8. Найти объём, ограниченный поверхностью =.

17.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле , взятому по объёму V, и заданному так:

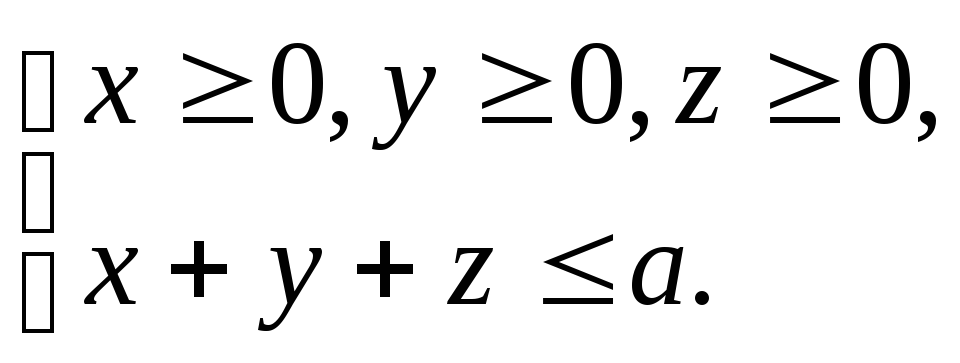
17.10. Определить высоту h прямоугольного параллелепипеда, в основании которого квадрат со стороной a, так, чтобы эллипсоид инерции для однородной массы, заполняющей этот параллелепипед, обратился в шар.

В А Р И А Н Т 18

18.1. Определить пределы интегрирования в двойном интеграле)ds в

декартовых и полярных координатах, если область определяется так:

18.2. В интеграле область интегрирования–четверть круга:,x>0, y>0. Заменой переменных превратить её в равнобедренный прямоугольный треугольник.

18.3. Записать двойной интеграл и вычислить площадь, ограниченную линиями y=lnx, x-y=1 и y=-1.

18.4 Найти объём, ограниченный следующими поверхностями cz=xy, x²+y²=ax, z=0; y>0.

18.5. Вычислить объём, ограниченный поверхностями az=a²-x²-y², z=0 (перейти к полярным координатам).

18.6. Найти величину поверхности (x+y)²+2z²=2a при x>0, y>0, z>0.

18.7. С помощью замены переменных найти объём тела, ограниченного поверхностями: x+y+z=a, x+y+z=2a, x+y=z, x+y=2z, y=x, y=3x.

18.8. Найти объём, ограниченный поверхностью =.

1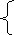8.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле dv, взятому по объёму V и заданному так:

x²+ y²+z²≤a²,

x²+y²≤ z²tg²α.

18.10. Доказать, что из всех эллипсов лишь у шара эллипсоид инерции есть шар.

В А Р И А Н Т 19

19.1. Определить пределы интегрирования в двойном интеграле ds в

декартовых и полярных координатах, если область определяется так:

x≥y; x+y≤2a; y≥0.

19.2. Вычислить двойной интеграл )ds по области s, границы которой определены так: x=0, y=0, x+y=2.

19.3. Построить области, площади которых выражаются:

1)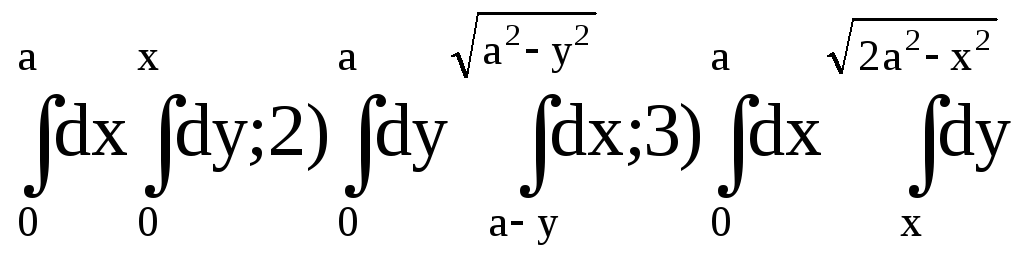, изменить порядок интегрирования.

Указание. Чтобы получить уравнение линий, ограничивающих область, нужно пределы интеграла по dx приравнять x, а пределы интеграла по dy приравнять y.

19.4. Найти объём, ограниченный следующими поверхностями z=x²+y²,

z = x + y.

19.5. Вычислить объём тела, ограниченного поверхностями az = a²-x²-y²,

z = 0.

19.6. Найти величину поверхности (x²+y²)z = x + y при 1<x²+y²<4, x>0, y>0.

19.7. С помощью замены переменных найти объём тела, ограниченного поверхностями a₁x+b₁y+c₁z=±h₁, a₂x+b₂y+c₂z=±h₂, a₃x+b₃y+c₃z=±h₃.

19.8. Найти объём, ограниченный поверхностью =.

19.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле dv, взятому по объёму V и заданному так:

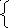x²+ y²≤z²,

x²+y²+z²=az.

19.10. Доказать, что для однородных тел, симметричных относительно плоскости yОz, величина J_xy=0.

В А Р И А Н Т 20

20.1. Определить пределы интегрирования в двойном интеграле ds

декартовых и полярных координатах, если область определяется так:

y²≤2px+p²; y≥x.

20.2. Вычислить двойной интеграл ds по области s, границы которой задаются так: y=0, x=y, x=1.

20.3. Построить области, площади которых выражаются интегралами:

1)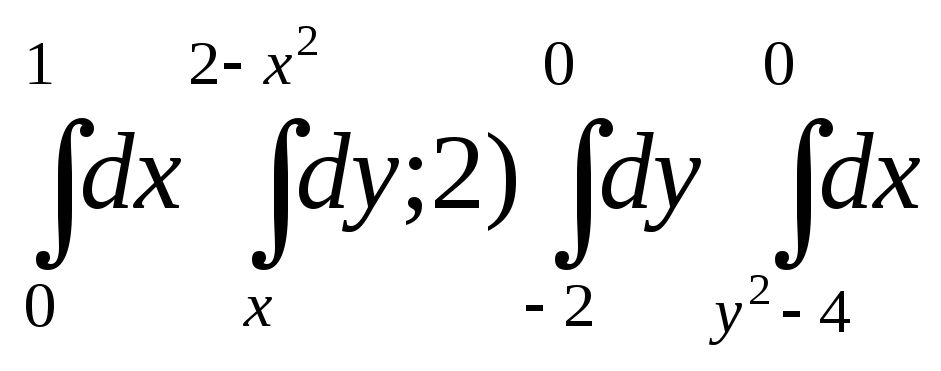. Изменить порядок интегрирования и вычислить площадь.

20.4. Доказать, что объём, ограниченный плоскостью z=mx+ny+p и параболоидом z=x²+y², равен половине площади круга x²+y²=mx+ny+p, умноженной на разность величин x²+y² = mx+ny+p, взятую в центре этого круга.

20.5. Вычислить объём тела, ограниченный поверхностями x²+y²+z²=4a², x²+y²=a² (вне цилиндра). Перейти к полярным координатам.

20.6. Найти величину поверхности +=2z внутри цилиндра +=1.

20.7. С помощью замены переменных найти объём тела, ограниченного поверхностями (a₁x+b₁y+c₁z)²+(a₂x+b₂y+c₂z)²+(a₃x+b₃y+c₃z)²=1.

20.8. Найти объём, ограниченный поверхностью =4;α²<1.

20.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле dv , взятому по объёму V и заданному так:

20.10. Доказать, что у однородных правильных многогранников эллипсоид инерции есть шар.

В А Р И А Н Т 21

21.1. Определить пределы интегрирования в двойном интеграле ds в

декартовых и полярных координатах, если область определяется так:

x²+y²≥a², x²+y²≤2ax.

21.2. Вычислить двойной интеграл по областиs, границы которой задаются так: x=y, x=y².

21.3. Вычислить площадь, ограниченную линиями r=a(1-cosφ) и r=a и расположенную вне круга.

21.4. Доказать, что объём сегмента, отсекаемого плоскостью от эллиптического параболоида, равен площади основания сегмента, умноженного на половину высоты сегмента.

21.5. Вычислить объём тела, ограниченного поверхностями x²+y²+z²=a², x²+y²±ax=0 (внутри цилиндра).

21.6. Найти величину поверхности -=2z внутри цилиндра +=1 при z>0.

21.7. С помощью замены переменных найти объём тела, ограниченного поверхностями (a₁x+b₁y+c₁z)²+(a₂x+b₂y+c₂z)²=1, a₃x+b₃y+c₃z=±h.

21.8. Найти объём, ограниченный поверхностью =

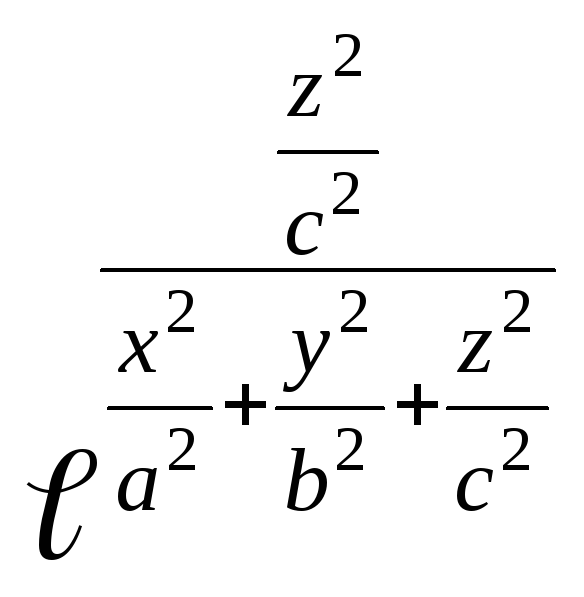
21.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле dv , взятому по объёму V и заданному так:

x²+ y²≤a²,

x+z=a,

z≥0.

21.10. Доказать, что однородный эллипсоид может быть подобен своему эллипсоиду инерции лишь в том случае, когда эллипсоид есть шар.

В А Р И А Н Т 22

22.1. Ввести вместо x и y новые переменные и определить пределы интегрирования по новым переменным :

, если u=x+y, uv=y.

22.2. Вычислить двойной интеграл

22.3. Вычислить площадь, ограниченную прямой rcosφ=a и окружностью r=2a.

22.4. От кругового конуса с радиусом основания R и высотой H отсечена часть плоскостью, параллельной оси конуса. Определить объём отсечённой части, если сегмент в основании соответствует центральному углу 2α.

22.5. Первым завитком геликоида y=xtg внутри цилиндра x²+y²=a² и плоскостью z=0.

22.6. Найти величину поверхности +=2z внутри цилиндра

= -.

22.7. С помощью замены переменных найти объём тела, ограниченного поверхностью │a₁x+b₁y+c₁z│+│a₂x+b₂y+c₂z│+│a₃x+b₃y+c₃z│=1.

22.8. Найти объём, ограниченный поверхностью =.

22.9. Определить пределы интегрирования в декартовых, цилиндрических и сферических координатах в тройном интеграле dv , взятому по объёму V и заданному так:

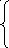x²+ y²≤z²,

x²+ z²≤a²,

z≥0.

22.10. Определить массу тела, ограниченного поверхностями x²+y²-z²=0 и z=h, если плотность в каждой точке равна аппликате этой точки.

В А Р И А Н Т 23

23.1. Ввести вместо x и y новые переменные и определить пределы интегрирования по новым переменным : , если u=αx+y, uv=y.

23.2. Вычислить двойной интеграл ,y=0, x=y, x+y=2,

границы области S

23.3. Вычислить площадь, ограниченную линиями xy=,xy=2a², y=, y=2x.

Указания. Перейти к новым координатам xy=u, y=vx, после чего площадь

определяется по формуле: ∫∫│J│dudv, где J= 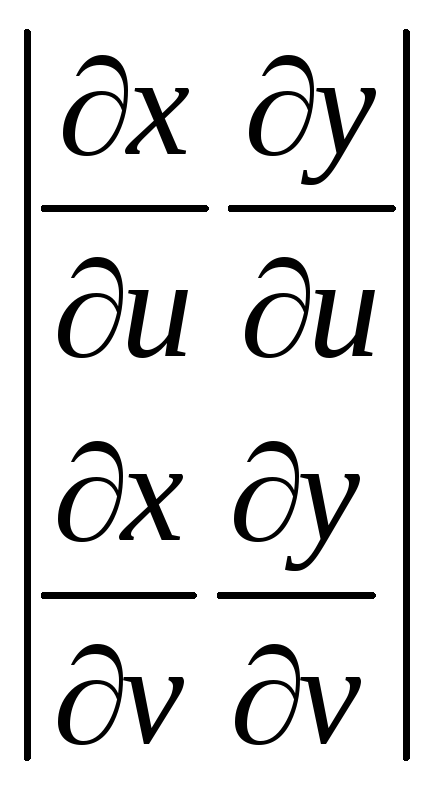– называется якобиан.

23.4. Правильная призма с квадратным основанием (со стороной а) и высотой h пересекается круговым конусом так, что след его на одном основании есть вписанная в основание окружность, а на другом основании –описанная около него окружность. Какая часть объёма призмы лежит вне конуса?

23.5. Вычислить объём тела, перейдя к полярным координатам: z²=2ax, x²+y²=ax.

23.6. Найти величину поверхности x²+y²+z²=a² при x>0, y>0, x+y<a, z>0.

23.7. Определить объём тела, ограниченного поверхностями az=x²+y²,

2az=a²-x²-y².

23.8. Найти объём, ограниченный поверхностью =.

23.9. Определить центр тяжести однородного тела, ограниченного поверхностями x+y+z=a, x=0, y=0, z=0.

23.10. Определить момент инерции относительно оси oz тела, ограниченного поверхностями x=0, y=0, y=a, z=0, x+z=a.

В А Р И А Н Т 24

24.1. Ввести вместо x и y новые переменные и определить пределы интегрирования по новым переменным : ∫∫ƒ(x,y)dxdy, x=rcos³φ, y=rsin³φ, а площадь S ограничена астроидой s

24.2. Вычислить двойной интеграл , границы областиS: y²=2x, x=2.

24.3. Вычислить площадь, ограниченную линиями y²=ax, y²=16ax, ay²=x³, 16ay²=x³.

Указания. Положить y²=ux, vy²=x³.

24.4. Правильная шестигранная призма (чайка) с шириной грани a пересекается сосной конической поверхностью, образующая которой составляет с осью угол α=60˚. Определить объём между боковой поверхностью призмы, её основанием и конусом, если конус пересекается с основанием по окружности, вписанной в основание.

24.5. Вычислить объём тела, ограниченного поверхностями =1--,z=0.

Указания. Перейти к обобщенным (эллиптическим) полярным координатам: x=arcosφ, y=brsinφ.

24.6. Найти величину поверхности z²=2xy при x>0, y>0, z>0, <1.

24.7. Определить объём тела, ограниченного поверхностями az=x²+y², z²=x²+y².

24.8. Показать, что поверхность конуса x²+y²-z²=0 делит объём шара x²+y²+z²=2az в отношении 3:1.

24.9. Определить центр тяжести однородного тела, ограниченного поверхностями az=a²-x²-y², z=0.

24.10. Определить момент относительно оси OZ тела, ограниченного поверхностями z²=2ax, z=0, x²+y²=ax.

В А Р И А Н Т 25

25.1. В интеграле площадь S ограниченна прямыми y=αx, y=βx,

x=a. Таким образом, область интегрирования треугольник. Подходящей заменой переменных обратить область интегрирования в прямоугольник.

25.2. Вычислить интегралы ,, предварительно изменив порядок интегрирования.

25.3. Вычислить площадь, ограниченную линией

Указания. Перейти к обобщенным полярным координатам: x=rcos³φ, y=rsin³φ.

25.4. Вычислить объём тела, ограниченного поверхностями az=a²-x²-y², z=0, x²+y²ax=0 (внутри цилиндра).

25.5. Вычислить объём тела, ограниченного поверхностями z=c, +=1.

25.6. Найти величину поверхности части геликоида x=rcosφ, y=rsinφ, z=hφ для 0<r<a, 0<φ<2.

25.7. Вычислить площадь поверхности параболы x²+y²=2az, расположенной внутри цилиндра x²+y²=3a².

25.8. Определить объём тела, ограниченного поверхностями az=x²+y², x²+y²+ z²=2a².

25.9. Определить центр тяжести однородного полушара x²+y²+ z²=2a², z=0.

25.10. Определить момент инерции относительно оси Oz тела, ограниченного поверхностями x+y+z=a, x²+y²=a², z=0.