5. Вычисление объёмов с помощью тройных интегралов

Основным методом решения задач, в которых требуется найти объем тела, ограниченного данной поверхностью, является введение соответствующих новых переменных, упрощающих интегрирование.

Пример. Найти объем, ограниченный поверхностями , , , где α<β.

Область изменения переменных характеризуется неравенствами: , .

Введем сферические координаты по формулам: , , .

При этом якобиан удобно вычислить по формуле J=J₁J₂, где J₁ –якобиан преобразования , , z=z, равный ρ (J₁= ρ), а J₂ - якобиан преобразования , , φ=φ, равный r. Таким образом, .

Область новых переменных характеризуется следующими неравенствами: , .

Так как z>0, то и cos θ>0, поэтому окончательно имеем неравенства: , .

Таким образом, при любых данных r и θ переменное φ может иметь любые значения от 0 до 2π, переменное r может при данном θ изменяться от 0 до 2acosφ, а угол θ может изменятся от α до β. Итак, объем вычисляем по формуле:

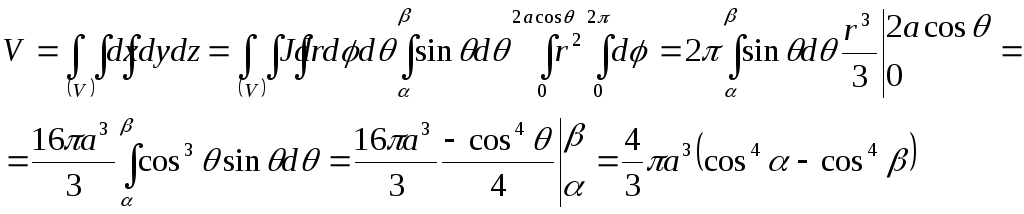
К практическим приложениям кратных интегралов относятся вычисления координат центра тяжести и моментов инерций тел.

6. Вычисление координат центра тяжести и моментов инерции тел с помощью тройных интегралов

6.1. Координаты центра тяжести тела, занимающего объем V, определяются формулами:

, , , _(5.1)

где ρ – плотность тела в точке (x,y,z), а m – масса тела:

. _(5.2)

Пример. Найти центр тяжести однородного тела, ограниченного сферой и параболой .

В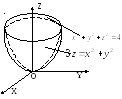оспользуемся формулами (5.1) и (5.2), в которых положим ρ=1. Тело симметрично, центр тяжести лежит на осиOz, поэтому и необходимо найти аппликату центра тяжести тела, т.е. . Т.к. тело симметричное, то в цилиндрической системе координат определяющие неравенства запишем в виде (рассмотрим первую четверть координатной системы.):

(V₁): ,,, а интеграл в виде

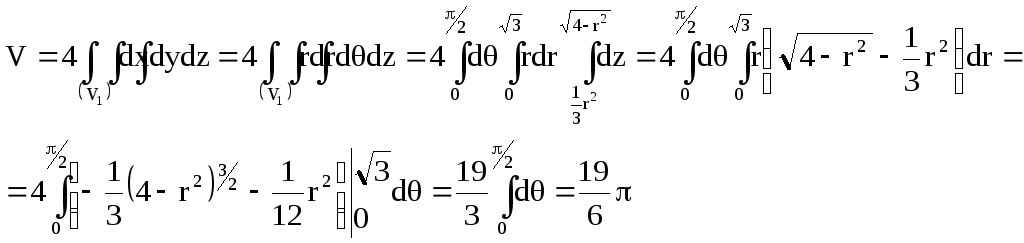
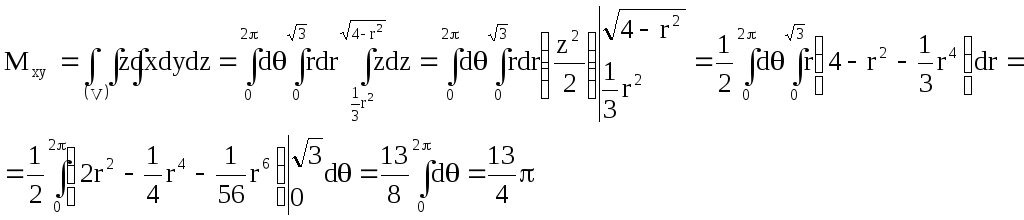
Следовательно, . Таким образом, центр тяжести данного тела находится в точке .

Замечание. Неравенства, определяющие область V₁ получены следующим образом. Уравнение 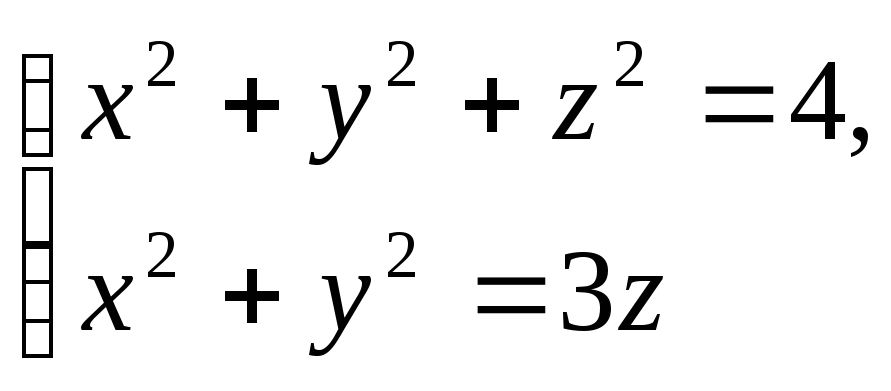определяется пересечением параболоида и сферы . Откуда, , z=1 и в цилиндрической системе координат . Следовательно, ; функции,; а.

Необходимо отметить, что при решении данной задачи не было необходимости выполнять чертеж. Достаточно записать неравенства, определяющие область V. Однако чертеж для наглядности приведен на рис.

6.2. Моментом инерции относительно некоторой оси L называют интеграл , гдеl – расстояние переменной точки тела (x,y,z) до оси.

Моменты инерций относительно координатных осей даются формулами: ,,.

Для однородных тел ρ=1. Центробежные моменты инерции определяются интегралами:

, ,.

Пример. Найти момент инерции куба со стороной a относительно его ребра.

Решение. Выбираем систему координат, начало которой точку O поместим в одну из вершин. Тогда неравенства, определяющие область интегрирования запишем в виде:

(V): ,,.

Момент инерции куба относительно ребра в такой системе координат можно вычислить, воспользовавшись формулой п.6.2, где . В данном случае ребро куба выбрано вдоль осиOX. Итак:

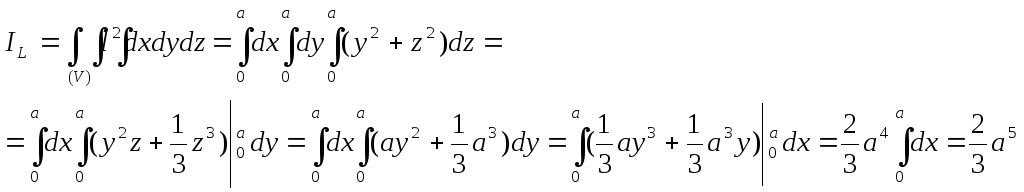
Задача решена. Отметим так же, что и в этой задаче не было необходимости выполнять чертеж. Достаточно записать неравенства, определяющие область.