10

Типовые задачи по разделу "ДИФОП".

1. Вычислить f ^'(a), в том числе для функции, заданной параметрически.

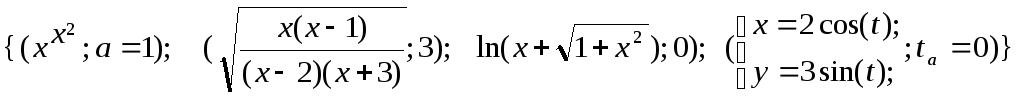
2. Записать уравнение касательной прямой к графику функции в заданной точке

3. Используя формулу Тейлора, вычислить приближенное значение функции в точке b=a+0.01.

4. Используя формулу Тейлора, исследовать свойства функции и схематически изобразить график функции в окрестности точки.

5. Найти интервалы монотонности функции.

6. Найти интервалы выпуклости и вогнутости функции.

7. Доказать неравенство f(x) > g(x) на заданном промежутке (a;b).

8. Найти точки локального экстремума функции.

9. Найти наибольшее и наименьшее значения функции на замкнутом промежутке.

10. Исследовать непрерывность и точки разрыва функции.

11. Найти точки перегиба графика функции.

12. Используя правило Лопиталя, вычислить предел ( "0.";" - "; 1

( sin(x-1).tg(πx/2); x1); (1/arctg(x) - 1/x); x0); (x^sin(x); x+0); (x^1/x;x); (1+1/x²)^x; x)

«Заочный экзамен».

1. Экз.: доказать 2,4,5,6,7 таблицы производных элементарных функций.

2. ЭКЗ. :доказать правила 2,3,4 дифференцирования функций.

Глава. Дифференциальное исчисление функции одной вещественной переменной.

1. §1 Производная функции в точке; полином и формула Тейлора 1 порядка; касательная прямая.

Воспоминания. (1) ( x)– б/малая при xa  lim( x)=0; (2) ( x)=o((x)) lim[( x)/ (x)]=0 при xa

(3) limf(x)=f(a)  f(x)-f(a) - б/малая при xa ; (4) ( x), (x) - б/малые при xa  ( x)(x)= o((x))= o((x))

P(x)=a_n(x-a)ⁿ+a_n-1(x-a)^n-1+…+a₁(x-a)+a₀ – полином степени “n”.

---------------------------------------------------------------------------

Пусть функция f непрерывна в точке х=а Û limf(x)=f(a) Û при х®а

a(x)=f(x)-f(a); b(x)=x -a бесконечно малые; рассмотрим предел их отношения в точке a:

Определение1. Если существует КОНЕЧНЫЙ предел отношения его называют производной функции f в точке х=а и пишут

(*)

Если же предел не существует или равен , говорят, что производная в точке не существует.

Например,

1)f: RR; f(x)=x² непр. x=aRf’(a)=lim(x²-a²)/(x-a)=lim(x+a)=2a

2) g: Rg(x)=; непр. а=-8g’(-8)=lim[(+2)/(x+8)]=(x-8)=

=lim[1/)(-2+4)]=1/12

3)

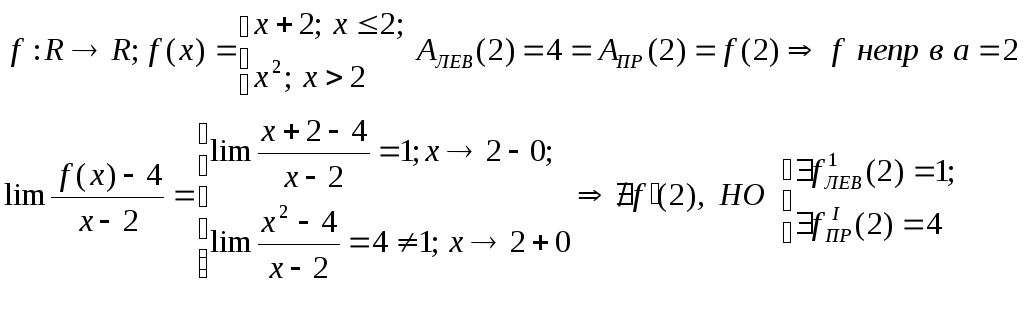
4)f=tg а=0-точка разрыва 2 рода (А_ЛЕВ=А_ПР=)не существует f’(0).

-------------------------------------------------------------------------

Следствия. f’(a)=lim[(f(x)-f(a))/(x-a)]

1.  (f(x)-f(a))/(x-a) – f’(a)=(x)- б/малая функция при xa

f(x)-[f(a)+f’(a)(x-a)]= (x)(x-a)o(x-a)

------ T₁(x,a)--- - полином первой степени

f’(a)

Определение. Полином (2)) называется полиномом Тейлора функции f в окрестности точки х=а, а равенство (1) называется формулой Тейлора 1-го порядка при xa.

Таким образом, если существует f’(a), значения функции f(x) при xa отличаются от значений полинома Тейлора T₁(x,a) на б/малую более высокого порядка малости чем (x-a).

Например, f(x)= ; a=-8  ;

f(-7.9)= T₁(-7.9;-8)=-2+0.1/12=-1.9917;|f(x)-T₁(x,a)|10^-4

---------------------------------------------------------------------------

2. Геометрически, отношение [f(x) - f(a)] / (x - a) = tg(a) определяет тангенс угла наклона секущей АВ {B(x,f(x); A(a,f(a) } графика y=f(x).

a

Предельное положение секущей АВ при х ®а определяет касательную прямую к графику в точке (a, f(a)) y_кас=f(a)+f’(a)(x-a), причем

• тангенс угла наклона касательной равен значению производной функции в точке;если f’(a)=0 _КАС=0–горизонтальная касательная

• касательная является графиком полинома Тейлора y=T₁(x,a)

В дальнейшем будем отождествлять существование производной в точке и существование касательной к графику функции в точке A(a,f(a) ).

=============================================================

Например, f(x)=x²; f(1)=1; f’(1)=2  y_кас=1+2(x-1); _{кас =} arctg(2)63^о

• ^{угол наклона касательной к графику y=x2в точке A(1,1);}

g(x)= ; a=1G(1)=1; G’(1)=1/3; y_k=1+; _{кас =} arctg(1/3)18^о

2. §2 Производная функция; производные элементарных функций; “арифметические” правила дифференцирования функций.

Пусть f: D_fRR; f(x)- непрерывная функция.

Если "aÎD_f’ÌDf $f’(a), то на множестве D_f’ определена производная функция

Например,

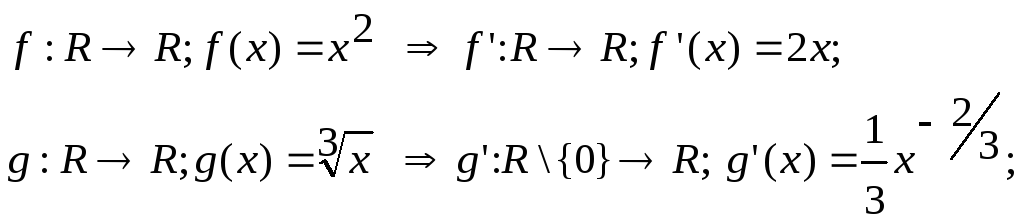
Таблица производных элементарных функций

f(x)	f’(x)	f(x)	f’(x)
1) x	 x-1	4) sin(x)	Cos(x)
x	1	5) cos(x)	-sin(x)
;x0	1/2;x>0	6) tg(x) xR/{/2+k;kZ}	1/cos2(x)
		7) ctg(x)	-1/sin2(x)
2) ax	axln(a)	8)arcsin(x) |x|1	1/
ex	ex	9)arcos(x) |x|1	1/
3)loga(x);x>0	1/(xln(a)	10) arctg(x)	1/(1+x2)
ln(x)	1/x	11) arcctg(x)	-1/(1+x2)

Докажем,например,

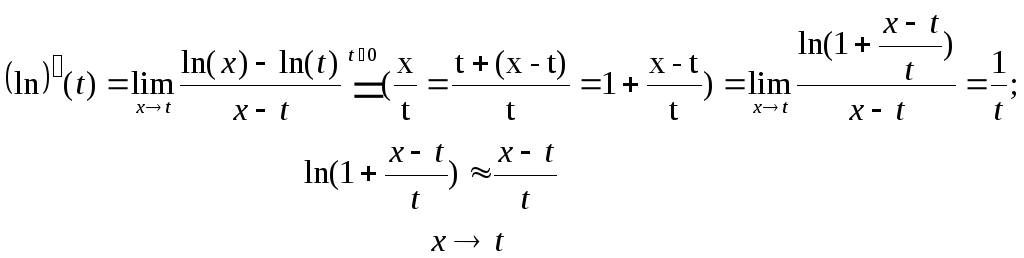
Экз.: доказать 2,4,5,6,7

Из определения производной функции и свойств пределов следуют «арифметические» правила вычисления производных :

(1) (с)’=0 – производная функции-константы;

(2) (cf(x))’=cf’(x);

(3) (f+g)’(x)=f’(x)+g’(x) – производная суммы функций;

 (cf(x)+dg(x))’=cf’(x)+dg’(x)- производная линейной комбинации функций;

(4) (f₁f₂)’(x)= f₁’(x)f₂(x)+ f₁(x)f₂’(x) – производная произведения функций;

(5) - производная отношения функций.

Докажем, например,

5)

 

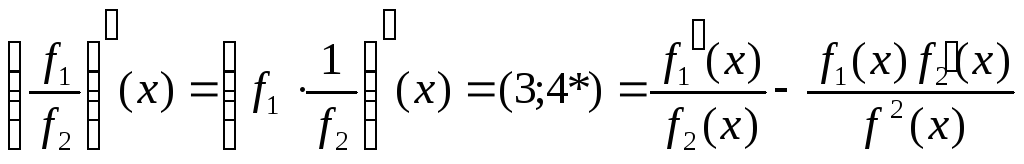
Например, (xsin(x))^’=(x)’sin(x)+x(sin(x))’=sin(x)+xcos(x);

(x/sin(x))’=[sin(x)-xcos(x)]/sin²(x)==

ЭКЗ. Доказать 1,2,3,4

Экз. задача. Для заданной функции:

1) определить производную функцию;

2) Записать уравнение касательной прямой к графику в точке; вычислить угол ее наклона к оси абсцисс и схематически изобразить “поведение” функции в окрестности точки;

3) Записать полином и формулу Тейлора в окрестности точки, вычислить приближенное значение функции в точке х=а0.01.

Например, f(x)=2e^x-3xcos(x); a=0.

1) f’: RR;f’(x)= 2e^x - 3(cos(x)-xsin(x));

2)f(0)=2;f’(0)=2 –3=-1=tg(_К) _К=arctg(-1)=-/4; у_К=2-(х-0)=2-x;

3) x1f(x)=T₁(x,0)+o(x-1); T₁(x,0)= 2-x;

f(1.01) T₁(1.01,1)=2 -0.01=1.99;f(1.01)=2e^.01-30.01cos(0.01)1.9901

Погрешность приближения f=f(0.01)-T₁(0.01;0)110^-4

3. §3 Производная суперпозиции функций; логарифмическая производная.

Пусть: 1) задана суперпозиция функций

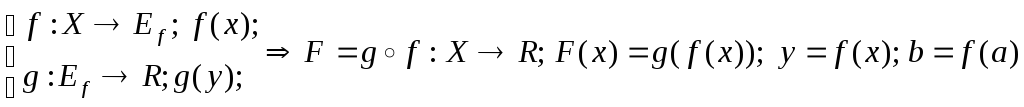
и 2) существуют производные f’(a), g’(b); b=f(a).

Теорема(производная суперпозиции функций).

«Если (1) f’(a) и (2) g’(b=f(a)), то (gf)’(a)=g’(b)f’(a)»

Док-во.

Обозначим y=f(x); b=f(a). Из существования производных f’(a) и g’(b) следует непрерывность функций f и g в точках x=a и y=b, т.е.

По определению производная суперпозиции g·f в точке х=а равна

Производная суперпозиции функций равна ПРОИЗВЕДЕНИЮ производных

составляющих эту суперпозицию функций.

Примеры.

1. f(t)=>f’(t)  [f(ax+b)]’=f’(t)(ax+b)’=f’(ax+b)a: [(2x-3)³]’=32(2x-3)²

f(x)=sin²(3x)=()² sin(3x)  f’(x)=2sin(3x)cos(3x)3=3sin(6x)

3.

xx²  ln(x²)  sin(ln(x²))

==================================================================

Замечание. Из основного логарифмического тождества A=e^ln(A)

 (а)f(x)>0; f(x)=e^ln(f(x)) , (б) (e^t)’=e^t и (в) производной суперпозиции

[e^t(x)]’=e^tt’(x) следует формула, которую называют «логарифмической производной» функции

f^'=e^ln(f(x))´[ln(f)]^' = f(x)´[ln(f)]^'

Эта формула «полезна» при вычислении производных произведения, отношения функций и производной степенно-показательной функции f(x)^g(x).

====================================================================

Например,

2)

f^'(Ö2)=2Ö2 ln(2e);

4. §4 Свойства функций, дифференцируемых на промежутке

5. (теоремы Ролля, Лагранжа).

Tеорема Ролля / без док./ Если функция f: a) непрерывна на замкнутом промежутке [a,b]; б) дифференцируема внутри него x(a,b)f^'(x) и в) принимает на концах промежутка равные значения f(a)=f(b), то внутри промежутка существует точка cÎ(a,b) ,касательная к графику y=f(x) в которой горизонтальна (производная f^/(c)=0).

f[a,b] непр.@ $f^/[(a,b)] @ f(a)=f(b) Þ $c Î(a,b): f^/(c)=0

Все три условия теоремы существенны !!!

x

d b a b

) A_левf(b) f(a) f(b)

a c b

Теорема Лагранжа Если функция f : a) непрерывна на [a,b];

b) диффернцируема на (a,b); то

внутри промежутка существует точка cÎ(a,b) , касательная к графику y=f(x)

в которой параллельна хорде АВ, соединяющей точки A(a,f(a)) и B(b,f(b)),

y

f(b) B

f(a) A

a c b x

Док-во. Функция F(x)= 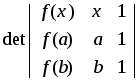=f(x)(a-b)-x(f(a)-f(b))+1(bf(a)-af(b))=

удовлетворяет т. Ролля : 1) f(x), x - непр.; на [a,b]; 2) дифф. на (a,b) и 3) F(a)=F(b)=0;

: $с Î(a,b) :

Cледствие. Если f удовлетворяет т.Лагранжа на [a,b], она удовлетворяет ей и на любом промежутке [x,xo]Ì[a,b] , поэтому имеет место

ФОРМУЛА ЛАГРАНЖА (формула конечных приращений )

СРАВНИТЕ !! формулы ЛАГРАНЖА и ТЕЙЛОРА для дифференцируемой функции f: