2. Геометрический смысл двойного интеграла

2.1. Если положить всюду в области, то получим выражение площади областив виде двойного интеграла:

. (2.1)

Действительно, непосредственно из определения интеграла следует, что:

.

Соответствующие задания функций приводят к вычислению двойного интеграла, значения величин и смысл которых рассмотрены ниже, в частности п.п. 3-4, там же приводятся рабочие формулы.

2.2. Аналогично задание функции приводит к выражению объема областив виде тройного интеграла. Это и естьгеометрический смысл тройного интеграла. Некоторые задания функции приводят к вычислению тройных интегралов, смысл которых рассматривается в п.п. 5-6.

3. Вычисление площадей с помощью двойных интегралов

3.1. Если область определена неравенством ,то площадь.

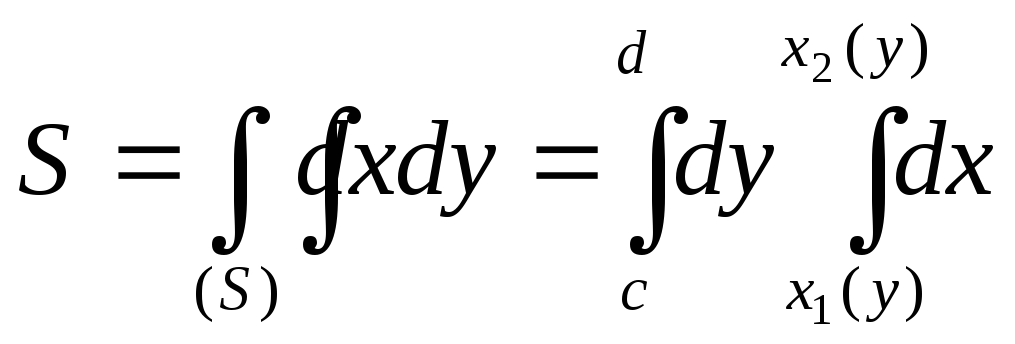3.2. Если область определена в полярных координатах неравенствами,, то площадьэтой области вычисляется следующим образом. (3.1)

Пример 1. Записать двойным интегралом и вычислить площадь, ограниченную линиями ,,.

Д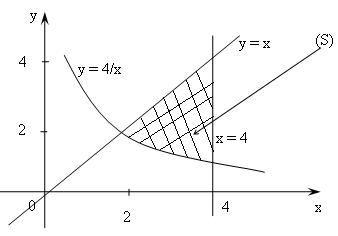ля решения задачи полезно сделать чертеж. В декартовой системе координатпостроим линии,,. Область, ограниченная этими линиями на рис.1 заштрихована. Далее необходимо определиться с порядком интегрирования и определить пределы интегрирования переменных. Если порядок интегрирования – сначала по, затем по,то областьопределяется неравенствами,, а площадь

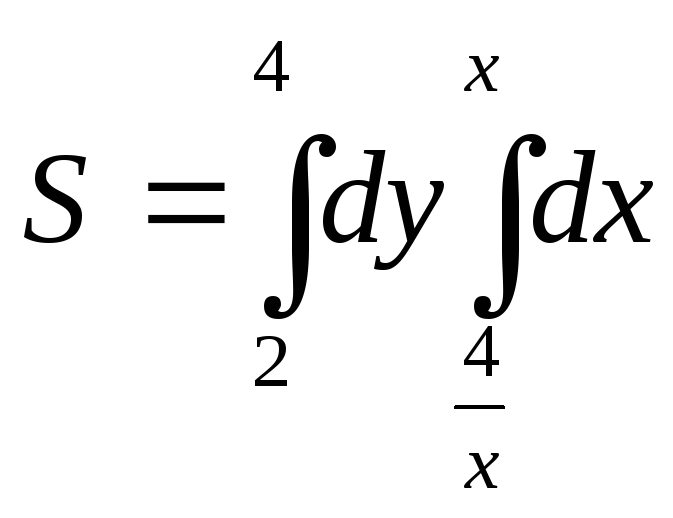. (3.2)

Остается вычислить интеграл (3.2):

Рис 1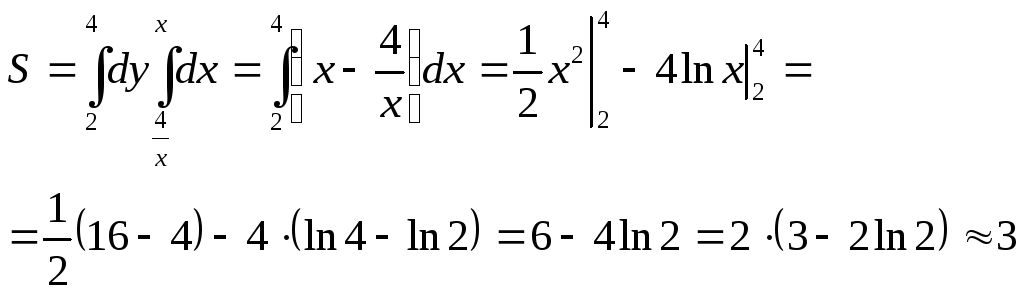

Задача решена. Если изменить порядок интегрирования, т.е. сначала по , а затем по, то областьопределяется неравенствами:

,и,, а площадь:

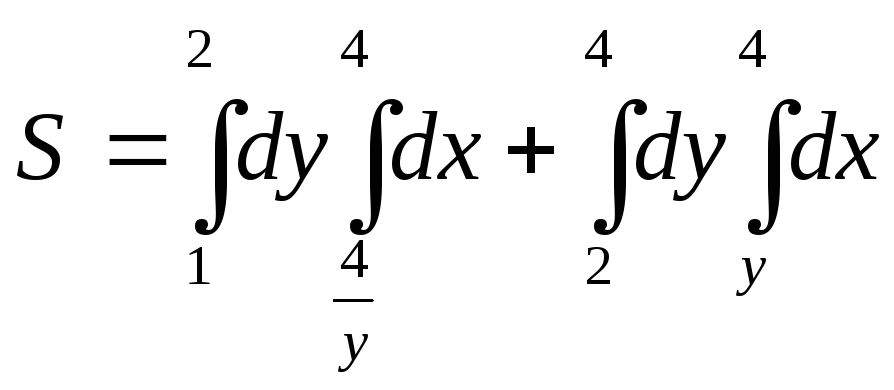. (3.3)

Вычисляя (3.3), получим:

Задача решена. Следует отметить, что удачный выбор порядка интегрирования позволяет решать задачи более рационально.

Использование полярных координат, иногда существенно упрощает определение площадей. При этом используется формула (3.1). В частности в задачах под номером 2 в вариантах 8–16 (8.2–16.2) полезней применять обобщенные полярные координаты, полагая ,, где– соответственно, выбранные постоянные. При этом якобианудобно вычислить по формулегде– якобиан подстановки,, равный,а– якобиан подстановки,равный величине.

Следует напомнить, что если ,, где– некоторые независимые переменные, то по определению Якобианвычисляется по формуле

By def

В задачах под номером 3 в вариантах 1-11 (1.3-11.3) границы площади заданы уравнениями вида ,,,. В них удобно выразитьичерез новые переменныеииз уравнений:,. Решая задачи, следует найти якобиани вычислить площадьпо формуле:.

4. Вычисление поверхностей, интегралов по поверхности, координат центров тяжести и моментов инерции поверхностей.

Из практических приложений двойных интегралов следует отметить вычисление поверхностей, интегралов по поверхности, координат центра тяжести и моментов инерции поверхностей.

4.1. В частности, величина поверхности, заданной уравнением определяется интегралом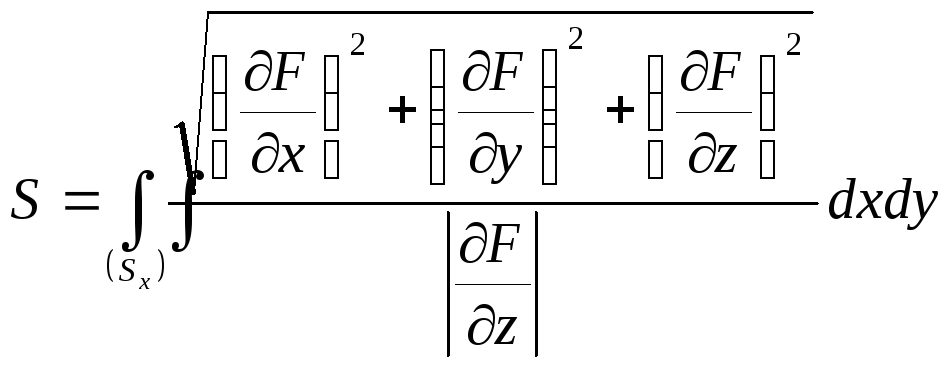, где площадьесть проекция искомой части поверхности на плоскость.

Аналогично, при проектировании на две другие координатные плоскости получим ту же величину поверхности по формулам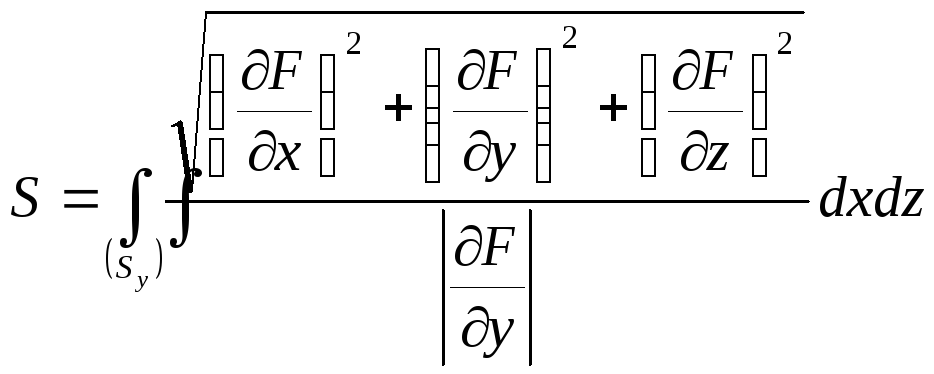(4.1)

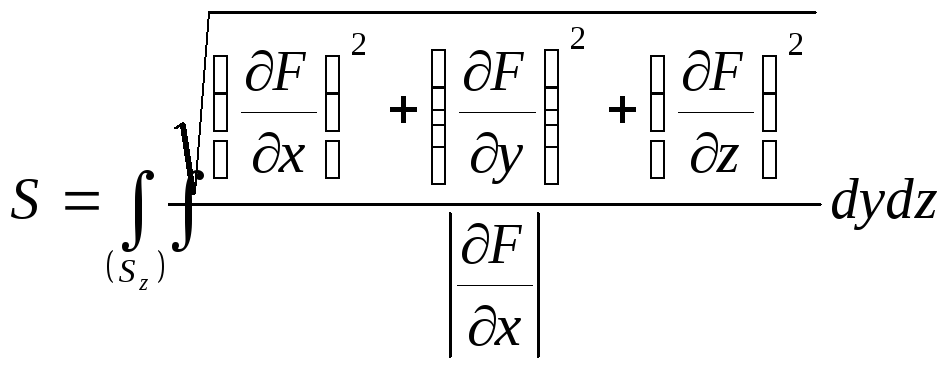(4.2)

Если поверхность задана параметрическими уравнениями ,,, а элемент дугикривой, лежащей на поверхности, выражается формулой, где,,, то величина поверхности представляется интегралом, распространенным на область значенийи, соответствующих точкам изучаемой части поверхности.

Пример. Вычислить площадь поверхности , расположенной внутри цилиндра.

Уравнение поверхности имеет вид:. Вычислим,,и.

; ;;. Для вычисления величины поверхности составим интеграл

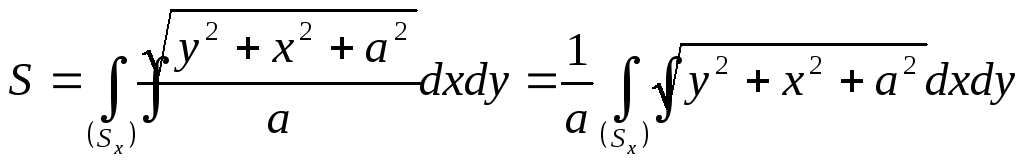(4.3)

Чтобы вычислить интеграл необходимо:

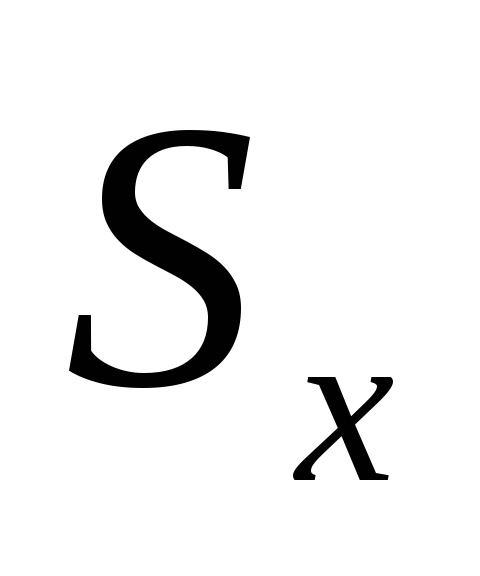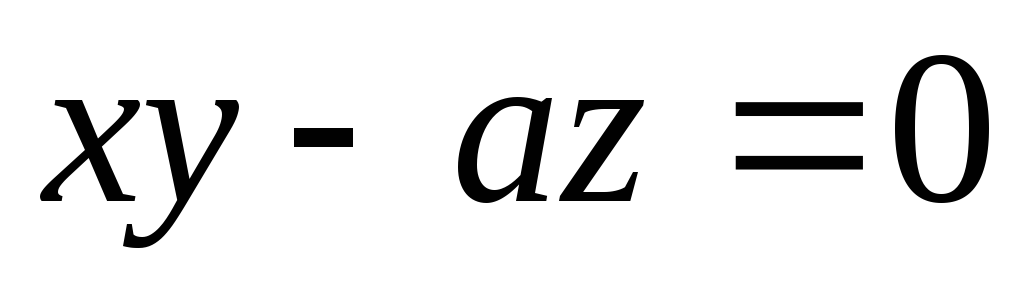1. определить область , являющейся проекцией поверхностина плоскость;

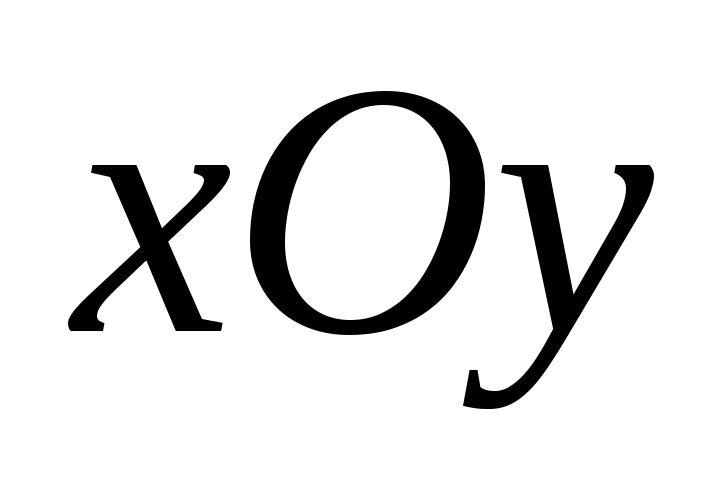2. определить порядок интегрирования;

3. определить пределы интегрирования.

Запишем уравнение линии пересечения поверхности и цилиндра. Это уравнение получается из пересечения поверхностей

.

Имеет вид . Понятно, что не может быть больше . Следовательно,x меняется в интервале , т.е. ; аy от до , т.е. область S_x определяется неравенствами , . Однако, интеграл (4.3) удобно вычислить, перейдя к координатам , . При таком выборе координат изменяется от 0 до,r – от 0 до 1, а .

Итак, .

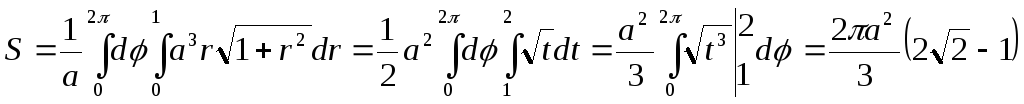Задача решена. Следует отметить, что при её решении не было необходимости выполнять чертеж. Его построение не определялось условием задачи. Однако, если при решении задачи без соответствующих чертежей, рисунков возникают затруднения в определении границы области и определении соответствующих неравенств, то чертежи и рисунки необходимо выполнить.

Следует отметить также, что использование формул (4.1) или (4.2) в данной задаче привели бы к более громоздким вычислениям, в чем не трудно убедиться самостоятельно.

4.2. Интегралом по поверхности называется интеграл вида

.

При его вычислении переменные x, y, z выражают через две независимые переменные, пользуясь уравнением поверхности или ее параметрическими уравнениями , , . Другая более отчетливая, формула интегралов по поверхности имеет вид:

,

где α, β, γ – углы нормали с осями координат. Если направление нормали изменить на обратное, то интеграл изменит знак на обратный.

Пример. Определить момент инерции части x>0, y>0, z>0 поверхности шара относительно оси Oz.

В задаче необходимо вычислить интеграл по поверхности , взятый по данной части поверхности шара. Найдем по формуле 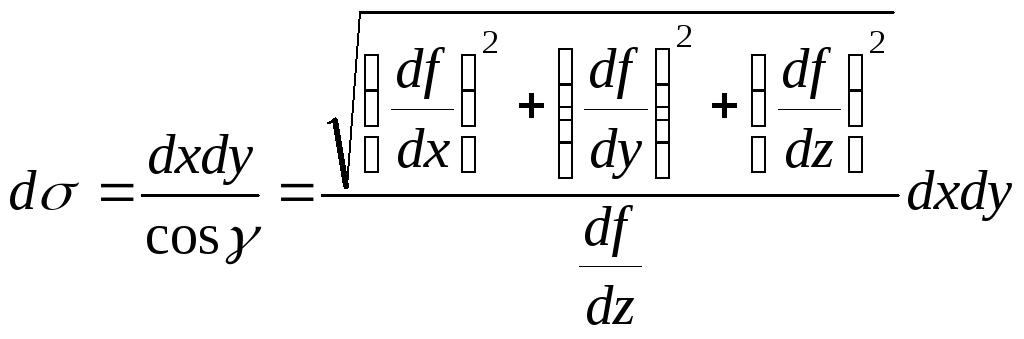, т.к. , то .

После этого получаем равенство:

,

где интеграл в правой части взят по четверти круга при x>0, y>0.

Вычислить интеграл гораздо удобнее, если координаты точек шара выразить через полярные углы φ и θ по формулам: , , . При этом , , а интеграл .

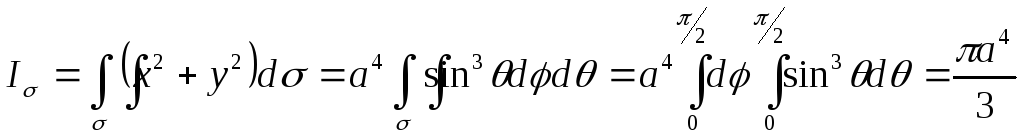4.3. Момент инерции площади S относительно какой-нибудь оси, лежащей в той же плоскости, называется интеграл , где δ – расстояние точки (x,y) до оси, а интеграл взят по всей площади S.

В частности моменты инерций относительно осей Ox и Oy равны интегралам: и .

Полярным моментом площади S относительно некоторой точки называется интеграл , где r – расстояние точки (x,y) до данной точки. В частности полярный момент относительно начала равен .

(Пример определения момента инерции по S см. п. 4.2.).

Центробежным моментом называют интеграл .

4.4. Нахождение координат центра тяжести частей однородных поверхностей, имеющих массу, выполняется с помощью интегралов по поверхности по формулам:

, , , ,

где S – данная часть поверхности.