18. Записать и пояснить физический смысл волновой функции.

Волнова́я фу́нкция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному): ,где — координатный базисный вектор, а — волновая функция в координатном представлении.Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

19. Вывести выражение, определяющее длину волны де Бройля – д.

Если частица имеет энергию E и импульс p, то с ней связана волна, частота которой = E/h и длина волны , где h " 6-10-27эрг-сек - постоянная Планка. Эти волны и получили название В. де Б. , 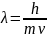(где m и - масса и скорость частицы). Таким образом, длина В. де Б. тем меньше, чем больше масса частицы и её скорость. Например, частице массой в 1 г, движущейся со скоростью 1 м/сек, будет соответствовать В. де Б. с l " 10-18 Å, что лежит за пределами доступной наблюдению области. Поэтому ясно, что волновые свойства несущественны в механике макроскопических тел.

20. Как де Бройль обосновал правило квантования момента импульса в третьем постулате Бора?

Третий постулат Н. Бора определяет правила квантования стационарных орбит. Бор предположил, что момент импульса электрона, вращающегося на стационарной орбите в атоме водорода, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде:

где me – масса электрона, υ – его орбитальная скорость, rn – радиус n-ой стационарной орбиты. Целое число n называется квантовым числом.

Правило квантования орбит по Бору получило наглядную интерпретацию в теории де Бройля, высказавшего гипотезу о наличии у электрона волновых свойств (1924 г.). Согласно де Бройлю электрону (и любому другому микрообъекту) соответствует волновой процесс с длиной волны ,где p – импульс электрона.

21. Найдите зависимость длины волны электрона от ускоряющего напряжения электрического поля, в котором он находится.

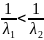
С уменьшением напряжения электрического поля, длина волны электрона увеличивается.

В классической механики рассматриваются большие длины волн и объекты, обладающие минимальной энергией.

22. Физические основы явления дифракции электронов в опытах к. Дэвиссона и л.Джермера (схема установки, выводы).

Проводилось исследование отражения электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, с ошлифованный под углом и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке:

Под углом к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.

В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния от азимутального угла , от скорости электронов в пучке.

Опыты показали, что имеется ярко выраженная селективность (выборочность) рассеяния электронов. При различных значениях углов и скоростей, в отражённых лучах наблюдаются максимумы и минимумы интенсивности. Условие максимума:

Здесь d — межплоскостное расстояние.

Таким образом наблюдалась дифракция электронов на кристаллической решётке монокристала. Опыт явился блестящим подтверждением существования у микрочастиц волновых свойств.