2.2. Основные законы и уравнения динамики жидкости

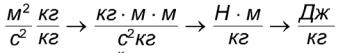
vk.com/club152685050 | vk.com/id446425943

30

Это выражение называется уравнением Бернулли в дифференциальной форме для элементарной струйки идеальной жидкости.

Интегрируя (2.36), получаем:

Уравнение (2.37) называется уравнением Бернулли (интегральной формой) для элементарной струйки идеальной жидкости

2.2.3. Геометрический и физический (энергетический) смысл уравнения Бернулли

Выясним сначала физический смысл величин, входящих в уравнение Бернулли. Любое правильное физическое соотношение размерностно однородно, т.е. все его члены имеют одинаковую размерность, поэтому достаточно рассмотреть один из его членов. Наиболее удобно обратиться к третьему – U2/2. Эта величина выражается в м2/с2. Умножим и разделим числитель и знаменатель на кг, что дает:

Из чего следует, что каждый член уравнения выражает энергию, отнесенную к единице массы, т.е. удельную энергию. Это позволяет придать уравнению Бернулли энергетический смысл. Первые два члена выражают удельную потенциальную энергию (положения – gZ и давления – p/ρ), а третий – удельную кинетическую энергию. Следовательно, полная удельная энергия в любом сечении струйки остается неизменной. Другими словами, уравнение Бернулли выражает закон сохранения энергии в ее простейшей форме - форме сохранения механической энергии.

Рассмотрим элементарную струйку движущейся жидкости.

Для двух произвольных поперечных сечений струйки можно записать

Разделив обе части уравнения (2.38) на ускорение свободного падения, получаем

vk.com/club152685050 | vk.com/id446425943

31

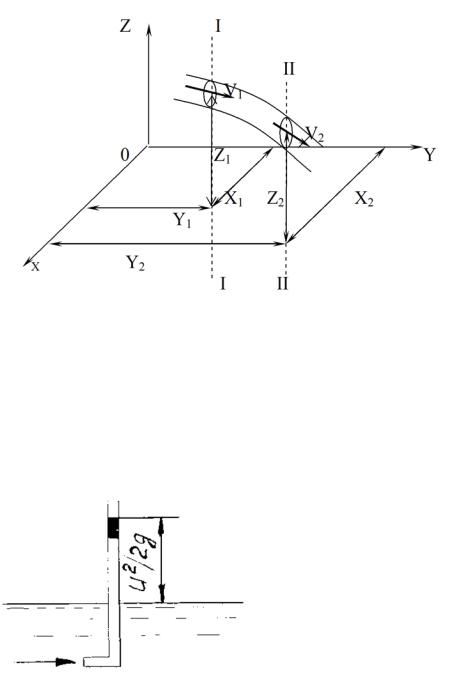
Каждый член (2.39) имеет линейную размерность и выражает напор, под которым в общем случае понимают высоту столба жидкости, уравновешивающую давление в данной точке. Таким образом, Z – геометрический напор, характеризующий положение жидкой частицы над какой-то произвольной плоскостью, называемой плоскостью отсчета; p/ρg - пьезометрический напор - высота столба жидкости, уравновешивающая давление в данной точке; U2/2g - скоростной напор, представляющий собой высоту столба жидкости в так называемой трубке полного напора (трубке Пито). Принцип действия этого устройства легко уясняется из рис.

что то же самое, полный либо гидродинамический напор при движении вдоль струйки остается неизменным. Сказанное иллюстрируется следующий рис., который иногда называют диаграммой уравнения Бернулли.

На рис. N-N- напорная линия; 0-0 - плоскость (линия) отсчета; Р-Р - пьезометрическая линия, лежащая ниже напорной на величину скоростного напора в данном сечении.