23. Продольные и поперечные волны.Дифференциальное волновое уравнение

Продольные волны-волны,в которых частицы колеблются в направлении распространения волны,т.е.вдоль луча.

Поперечные волны-волны,в которых частицы среды колеблются в направлении,перпендикулярном к направлению распространения волны,т.е.перпендикулярно к лучу.

= ,где ∆- оператор Лапласа,u=u(x,t)-неизвестная функция, v- фазовая скорость.

25. Волновой пакет. Групповая скорость. Ф-ла Рэля.

Определим скорость перемещения максимумов амплитуды А(t,x),которая равна фазовой скорости модулирующей волны:

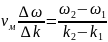
Поскольку плотность энергии двух складываемых бегущих волн определяется квадратом амплитуды результирующей волны, то скорость переноса этой энергии будет равна скорости , которую называют групповой скоростью:

Установим связь между групповой скоростью и фазовой скоростью результирующей волны( = 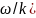.Поскольку , λ, а скорость при наличии дисперсии зависит от λ, то после перехода от дифференцирования по волновому числу к диффиринцированию по λ=2π/ получим искомое выражение:

(1)-ф-ла Релея. Из неё следует, что при нормальной дисперсии(dv/dλ групповая скорость меньше фазовой при аномалии(dv/dλ 0)-групповая скорость больше фазовой ,а при отсутствии дисперсии эти скорости равны.

Результирующая волна имеет целый ряд максимумов. При наложении достаточно большого числа волн с близкими частотами и волновыми числами можно избавиться от все максимумов, кроме одного. Для этого нужно спец.образом подобрать амплитуды волн, которые в соответствии с уравнением:

Определяют результирующее волновое образование с пространственной локализацией, называемое волновым пакетом. Скорость перемещения центра тяжести такого пакета определяется его групповой скоростью, а локализация ∆x π/𝙠 зависит от интервала волновых чисел ∆𝙠 пакета или соответствующего ему интервала частот ∆𝜔(∆x∆𝙠 π).Чем меньше ширина пакета,тем больший интервал волновых чисел ∆𝙠 требуется для его описания с помощью разложения.

21 Метод векторных диаграмм сложения гармонических

Метод векторных диаграмм

Колебания можно графически в виде векторов на плоскости. Изображенная таким способом схема колебаний называется векторной диаграммой.

Рассмотрим произвольный вектор а , образующий с осью Х угол альфа.

Если привести этот вектор во вращение относительно точки О с угловой скоростью ὠ₀ , то проекция конца вектора будет перемещаться по оси в пределах от +а до –а. Координата этой проекции будет изменяться со временем по закону

Х= А cos(ὠ₀ t + ϕ)

Проекция конца вектора a будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скоростиὠ_o вращения вектора, и с начальной фазой, равной ϕ . (углу, образованному вектором a с осью x в начальный момент времени).

Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью x угол, равный начальной фазе колебания.

Гармоническими называются колебания, при которых описываемая физическая величина изменяется по закону синуса или косинуса. Уравнение кинематики гармонических колебаний имеет следующий вид:

x = A·cos(2·t/T +₀),     (9.1) где х - колеблющаяся величина, t - время; А, Т,  - константы для данного колебания, называемые параметрами. 

Гармонические колебания являются частным случаем периодических колебаний

Сложение гармонических колебаний

        Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.

9. Работа и мощность.

Для характеристики действующей на тело силы F используется величина, называемая механической работой. Пусть под действием постоянной силы F тело переместилось из положения 1 в положение 2 (см. рис. 1). Перемещение характеризуется вектором S. Работой силы F на перемещении S называется скалярная величина, определяемая равенством: A = F · S ·cosa. 1 Дж = 1 Н·м. Мощностью (средней мощностью) называется величина, определяемая равенством N = A/t, где t – время действия силы. Очевидно, что N = F · V ·cosa. Это выражение справедливо также для расчета мгновенного значения мощности. Единица измерения мощности – Ватт. 1 Вт = 1 Дж/с.

7. Момент импульса материальной точки.Момент импульса телаМомент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: