
- •22. Вынужденное колебания. Резонанс.
- •17. Уравнение неразрывности. Уравнение Бернулли.
- •17 Вопрос: 1.Классическая теория теплоемкости твёрдых тел. Закон Дюлонга и Пти.
- •2.Закон Видемана- Франца. Вывод закона Видемана-Франца на основе классических представлений.
- •2Вопрос. 2.Закон Видемана- Франца. Вывод закона Видемана-Франца на основе классических представлений.
- •2. Нормальное и тангенцильное ускорение точки
- •23. Продольные и поперечные волны.Дифференциальное волновое уравнение
- •25. Волновой пакет. Групповая скорость. Ф-ла Рэля.
- •21 Метод векторных диаграмм сложения гармонических
- •12.Консервативные силы,потенциальная энергия.Связь между работой консервативных сил и потенциальной энергией.
- •16. Ламинарные и турбулентные режимы течения жидкостей и газов.
- •4. Угловые скорость и ускорение. Связь между линейными и угловыми характеристиками движения твердого тела.
22. Вынужденное колебания. Резонанс.
Вынужденными колебаниями -называются колебания ,возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Примером вынужденных колебаний могут служить колебания силы тока в электрической цепи, вызываемые переменной электро движущейся силы; колебания маятника . вызываемые переменной внешней силы.
Резонанс.Исследуем выражении
 и
и
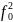 =(2
=(2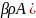 2+(
2+(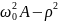 A)2
A)2
Как
функции частоты p и построим
их графики. Очевидно , что максимум А
соотвествует минимуму знаменателя или
подкоренного выражения по p,
получим уравнение
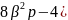 Его решение имеет три корня P1=0,
p2,3=
Его решение имеет три корня P1=0,
p2,3=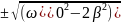 Из двух корней p2 и
p3 физический смысл
имеет лишь положительный корень,
определяющий резонансною частоту
внешней периодической силы.
Из двух корней p2 и
p3 физический смысл
имеет лишь положительный корень,
определяющий резонансною частоту
внешней периодической силы.
Pрез= ,
,
Который
соответствует максимальное (резонансое
) значение амплитуды вибратора :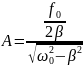
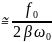 .
.
При частоте p, стремящейся к нулю, амплитуда А вынужденных колебаний стремится к значению

которое
определяет смещение точки из положения
равновесия при статическом действии
силы, равной Е0. При частоте p,
стремящейся к бесконечности амплитуда
А стремится к нулю по закону
 Покажем , что отношение Арез к
А(0) совпадает с добротностью уравнением:
Покажем , что отношение Арез к
А(0) совпадает с добротностью уравнением: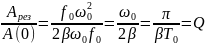
Зависимость
сдвига фазы
 вынужденных колебаний по отношению к
фазе pt возмущающей силы
вынужденных колебаний по отношению к
фазе pt возмущающей силы
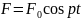 .
Резонансная частота всегда несколько
меньше собственной частоты, а значение
α при резонансе близко к π/2. В отсутствии
сопротивления(β=0)сдвиг фаз α скачком
меняется от нуля при p
.
Резонансная частота всегда несколько
меньше собственной частоты, а значение
α при резонансе близко к π/2. В отсутствии
сопротивления(β=0)сдвиг фаз α скачком
меняется от нуля при p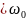 до π при p
до π при p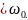
17. Уравнение неразрывности. Уравнение Бернулли.
Возьмем трубку тока настолько малой площади сечения S, чтобы можно было считать, что скорость жидкости v одинакова во всех точках этого поперечного сечения и направлена вдоль оси трубки .При стационарном течении за одно и тоже время dt через различные сечения трубки пройдет одинаковая масса dm жидкости, равная pvSdt, где p- плотность жидкости .Для двух сечений с площадями S1 и S2 получим:
P1 v1 S1 dt= p2v2S2dt или p1v1S1=p2v2S2
Полученное соотношение называется уравнением неразрывности. Оно справедливо для любых сечений данной трубки тока:
VS=const-уравнение неразрывности |
Следует, что скорости течения жидкости вдоль трубки тока обратно пропорциональны площадям её поперечного сечения. В сужающей части трубки тока скорость течения жидкости возрастает, а в расширяющейся- уменьшается, т.е. жидкость на этих участках движется с ускорением.
pv2/2+pgh+ p=const- уравнение Бернулли |
Выражает закон сохранения энергии стационарном течении несжимаемой идеальной среды. Каждое из слагаемых уравнения Бернулли имеет размерность давления: p- статическое давление, pgh-гидравлическое( весовое давление). Сумма динамического, гидравлического и статистического давлений при стационарном течении среды есть величина постоянная для всех точек данной линии тока. Статическое давление измеряют с помощью зонда- изогнутой трубки, передняя часть которой запаяна, а в боковой стенке небольшое отверстие. Динамическое давление совместно со статическим.
