
- •7.Формы записи задачи лп
- •8.Переход к канон.Ф.:
- •10.Геом. Интерпретация цф и ограничений задачи.
- •12. Геоминтерпр-ия задачи лп с несколькими переменными.
- •13Основная теорема лп
- •15. Построение начальн. Опорн. Плана
- •17.Переход к нехудшему опорному плану
- •18. Правила пересчёта
- •20.Призн.Неогр-ти цф на множ-ве планов.Геом.Интрепр.
- •21Прямая и двойственная задача
- •22.Основное неравенство теории двойственности и его экон. Содерж.
- •23.Критерий оптимальности Канторовича
- •27. Постановка тз по критерию стоимости.
- •28.Трансп-ная табл. Теорема о сущ-нии допуст плана.
- •29. Тз с закр. И откр.Моделью.
- •31. Правило «северо-западного угла»
- •32.Прав «миним эл-та» (наим стоим»)
- •33. Теор о потенц. Алг теор
- •35. Усложненные постановки тз.
- •41.Постр-е прав-го отсечения. Теорема о прав отсеч
- •42.Метод ветвей и границ.
- •43. Понят о дп. Принц оптим Беллмана
- •44. Вычисл схема реш задач методом дп
- •47. Задача оптим. Планирования вып-ка, сод-я и хран-я пр-ции и решение ее методом дин-го рогр-я
- •48. Задача замены оборуд
- •50.Метод множ Ланг-жа реш задач нп.Эк смысл множ Ланг-жа.
- •51.Градиент.Метод решения задачНп
22.Основное неравенство теории двойственности и его экон. Содерж.
Рассмотрим пару симметричных двойственных задач
maxF=∑cjxj
∑aijxj≤bi,i=1,m; i=1,m (1)
xj≥0,j=1,n
minϕ=∑biyi, i=1,m
∑aijyj≥cj, j=1,n; (2)
yi≥0, i=1,m
Теорема. Для любых допустимых планов Х=(х1,х2,…,хn) и Y=(y1,y2,…,ym) прямой и дв-ной задач ЛП справедливо неравенство
F(X)≤ϕ(Y), т.е.
∑cjxj≤∑biyi (3)
Доказательство:учитывая неравенства 1 и 2, получаем:
F(X)=∑cjxj(j=1,n)≤∑(j=1,n)(∑aijyi(i=1,m))xj=∑(i=1,m)yi∑(j=1,n)aijxj≤∑(i=1,m)biyi=ϕ(Y)
Эк-ое содержание теоремы: для любого допустимого плана производства Х и любого допустимого вектора оценок ресурсов У общая созданная стоимость не превосходит суммарной оценки ресурсов.
23.Критерий оптимальности Канторовича
Теорема. Если для некоторых допустимых планов Х* и У* пары дв-ных задач выполняется равенство F(X*)=ϕ(Y*),то Х* и У*- оптимальные планы соответственно.
Доказательство: согласно осн-му неравенству теорем дв-ти для любого допустимого плана Х прямой задачи и любого допустимого плана У* дв-ной задачи выполняется неравенство F(X)≤ϕ(Y*). Но по условию теоремы F(X*)=ϕ(Y*). Отсюда в силу транзитивности отношений «≤» и (=) имеем F(X)≤F(X*),но т.к. Х-произвольный допустимый план, то тогда F(X*)=maxF.Значит, Х*-оптим. план прямой задачи ЛП. Аналогично доказывается, что У* явл-ся оптимальным для дв-ной задачи.
Эк. содержание: план производства Х* и вектор оценок ресурсов У* явл-ся оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадает.
25. теор о доп-ей нежесткости и ее эк сод-ие. Теорема: для того, чтобы планы Х*, У* пары двойст-х задач были оптим-ми необх и достат вып-ие след-х усл-ий: хj*(∑аijyi*- сj)=0, j=1,n (1),yi*(∑аijxi*- bi)=0, i=1,m(2). Док-во: необход-ть махF =∑cjxj, ∑аijxi*= bi, i=1,m, xj≥0, j=1,n.(3) minφ= ∑biyi∑аijyi* ≥сj, j=1,n yi≥0, i=1,m. F (X*)=φ(Y*)т.е∑cjxj,*= ∑biyi*(4). Подставим в 4 biиз 3: ∑cjxj,*=(∑аijxi*) yi*= ∑хj*∑аijyi*→ ∑хj*(∑аijyi*- сj)=0 (5). Т.к хj*≥0, и ∑аijyi*- сj ≥0, j=1,n. След-но из рав-ва 5 след-т условие 1, усл 2 док-ся аналогично. Достат-ть: ∑хj*(∑аijyi*- сj)= ∑хj*∑аijyi*-∑cjxj,*= ∑yi*∑аijxi* - ∑cjxj,*= ∑biyi*- ∑cjxj,*→ F (X*)=φ(Y*). Эк содерж: Двойствоценки могут служ мерой дефицитности ресурсов (ДР).ДР, т.е ресурс по опт-му плану пр-ва исп-ся полностью имеет полож-ю оценку, а избыт-й имеет нулевую оценку.
26.Теорема
об оценках.Теорема:
двойств-е оценки показ-ют приращение
ЦФ, вызванное измен-ем св. члена соотв.
ограни. ∂F(X*)/∂bi=y*,
i=1,m.
(1).
Док-во:
Рассм. задачу вида:maxF=f(X)(2),
ϕi=bi,(i=1,m)(3).перейдём
от задачи на условн. экстремум к зад.
на безусл. экстрем. Для этого построим
вспом. функц. Лагранжа(фЛ):
L(X,Y)=f(X)+∑(m,i=1)yi(bi-ϕi(X))(4),
где yi
непред. множит. лагранжа. запишем
необходимые условия экстремума фЛ для
этого ищем часные производные фЛ по
xiиyi,
приравнив. к 0: 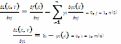
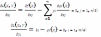 покажем
что всякое экстр. значение задачи(2,3)
удовл. услов. (5,6) Пусть Х*-допустим. план,
доставляющий ЦФ экстр. значение, то
покажем
что всякое экстр. значение задачи(2,3)
удовл. услов. (5,6) Пусть Х*-допустим. план,
доставляющий ЦФ экстр. значение, то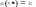 ,
i=1,m,
и услов. 6 выполняются, след-но из фЛ
следует: L(X*,Y*)=f(F*),
откуда
,
i=1,m,
и услов. 6 выполняются, след-но из фЛ
следует: L(X*,Y*)=f(F*),
откуда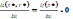 ,выполн. условие 5.Каждая доп. точка Х*
д\б решением системы,это необход. условие
для отыск. экстр.Пусть своб члены сист.
огран.(3) измен. в некот. пределах,
следов-но будет меняться и ЦФ. обозначим
коорд. крайних точек через:x1(B)=x1(b1,b2,…,bm),
x2(B)=x2(b1,b2,…,bm),…,
xn(B)=xn(b1,b2,…,bm).
рассм. фЛ, как функц. завис-щую от В:
L(B)=f(X(b))+∑(m,i=1)yi(bi-ϕi(X(B)))
(7).дифференцируя фЛ по biполучим:
,выполн. условие 5.Каждая доп. точка Х*
д\б решением системы,это необход. условие
для отыск. экстр.Пусть своб члены сист.
огран.(3) измен. в некот. пределах,
следов-но будет меняться и ЦФ. обозначим
коорд. крайних точек через:x1(B)=x1(b1,b2,…,bm),
x2(B)=x2(b1,b2,…,bm),…,
xn(B)=xn(b1,b2,…,bm).
рассм. фЛ, как функц. завис-щую от В:
L(B)=f(X(b))+∑(m,i=1)yi(bi-ϕi(X(B)))
(7).дифференцируя фЛ по biполучим:
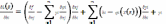 (8)
учитывая (5 и 6) из равенства (8)
(8)
учитывая (5 и 6) из равенства (8) 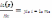 Но
для ОП L(X*,Y*)=f(X*),следовательно
Но
для ОП L(X*,Y*)=f(X*),следовательно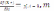 Эк.
содерж-е:
для этого в выраж-ии (1) дифференциалы
заменим приращениями, т.е. ∂bi≈∆bi,
∂z(x*)≈∆z(x*).
Получим ∆z(x*)=уi*∆bi;
при ∆bi=1
имеем ∆z(x*)≈yi*.
Отсюда двойств оценка числ-но равна
измен-ю ЦФ при измен-ии соотв. своб.
члена ограничений на ед.
Эк.
содерж-е:
для этого в выраж-ии (1) дифференциалы
заменим приращениями, т.е. ∂bi≈∆bi,
∂z(x*)≈∆z(x*).
Получим ∆z(x*)=уi*∆bi;
при ∆bi=1
имеем ∆z(x*)≈yi*.
Отсюда двойств оценка числ-но равна
измен-ю ЦФ при измен-ии соотв. своб.
члена ограничений на ед.
