1.Предмет и постановка общей задачи мат. Прогр-я – область прикладной математики, разраб-щая теорию и численные методы решения многомерных, экстрем-х задач с ограничением, т.е. задач на экстремум ф-ции многих переменных с ограничениеми на область измен-я этих переменных. ЭММ –система мат. ф-ций, уравнений, неравенств и т.д.,описывающих реал-й эконом-й объект, сставляющие его характ-ки и взаимосвязи м-ду ними. Модель задачи МП можно записать в виде: max (min)F= f(x₁,x₂,…x_n), (1); ϕ_i (x₁,x₂,…x_n) { ≤, =, ≥} b_i, i=1,m. (2); x_j≥ 0, j =1,n. (3) . 1 – ЦФ(показатель эффективности, критерий оптимальности) В качестве ЦФ мб прибыль, объем выпуска или реализации, отходы и т.д.; 2 – основные;3 – прямые ограничения. Матем-ки ограничения запис-ся в виде уравн-й и нерав-в, сов-ть которых образ-т ОДР. Сов-ть независимых величин Х=( x₁,x₂,…x_n), действуя на которые систему можно совершенств-ть, наз. планом задач. План Х, удовлетворяющий основным и прямым ограничениям наз-ся допустимым. Допустимый план, доставл-щий ЦФ экстрем. значение наз. оптимальным и обознач-ся Х*.Экстр.значение ЦФ обознач-сяF*=F(X*). В завис-ти от свойств ф-цийf и ϕ_i (i=1,m) МП можно рассматривать как ряд самост. величин. Задачи МП делятся на задачи линейного и нелинейного прогр-я.Отдел-ми класс-ми задач явл. задачи целочисл-го, параметрич-го, дробнолин-гопрогр-я.

2.Понятие ЛП – раздел МП, в котором разраб-ся методы отыскания экстр-малин-х ф-ций многих переменных при лин-х дополн-х огранич-ях, налаг-мых на эти перемен-е.

3.Постановказад.о.наилуч.исп.рес-в и ее экон. модель. Пусть производится n видов прод-и, при этом исп-етсяmрес-сов. Известны след.параметры:c_j,j=1,n – цена ед-цыпрод. j-го вида; b_i,i=1,m –имеющееся кол-во i-го рес-са; a_ij,j=1,n, i=1,m –расходi-го рес-са для пр-ва единицы прод-и j-го вида.Треб-сяопр-ть план пр-ва каждого вида прод-и X*=(x₁*,x₂*…x_n*), при кот. обесп-сяmax-аяст-сть всей пр-ции при имеющихся ресурсах.Так как c_{j –} цена ед-цыпрод-цииj-го вида, то цена x_jед-ц будет равна c_jx_j, а общая ст-сть всех nвидов прод-ции составит:F=c₁x₁+c₂x₂+…+c_nx_n.

Расход на пр-во всех n видов прод-и не должен превышать b_i:a_i1x₁+a_i2x₂+…+a_inx_n≤b_i, i=1,m.

Чтобы искомый план произ-ва был реален, нужно наложить усл-е неотриц-ти:x_j≥0, j=1,n.

Таким образом,ЭММ задачи о наилучшем исполь-ии рес-сов:maxF=

x_j≥0, j=1,n.

4.Постановка зад.о.диете и ее экономико-мат модель. Пусть имеется nпрод-овпитания, в кот. Содержится mполезных вещ-в.Известны след. параметры:c_j,j=1,n – ценаед-цыj-го прод-та; b_i,i=1,m – min-екол-воi-гополезноговещ-ва;a_ij, j=1,n,i=1,m–содерж-еi-гополезного вещ-вавед-цеj-гопрод-та.Треб-сяопр-тькол-воприобретениякажд. видапрод.X*=(x₁*,x₂*…x_n*),обесп-е необх.кол-во полез.вещ-в при min-ой общей стоим-ти продуктов питания.

ЭММ задачи о диете будет иметь вид:minF=

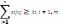
x_j≥0,j=1,n.

5.Постановка задачи о выборе оптимальных технологий и ее Эмм. В зада­че о наилучиспользрес-овопред-сяопти­м-ый план выпуска продукции. Пусть при произ-ве какого-то общественно необход продукта использ-сяnтехнологий. При этом треб-сят видов рес-ов, задан­ных объемамиb_i (i = 1, m).Эффек-ти технологий, т. е. кол-во конечной продукции (в ден. ед.), производ в ед. времени по j-й (j= 1,n)технологии, обозначим c_j.Пусть, далее,а_ij- — расход i-го ресурса в единицу времени по j-й технологии.В качественеизвестной величины x_jпри­мем интенсивность использj-й технологии, т. е. вре­мя, в течение которого продукция произв-ся по j-й техно­логии. Пренебрегая временем переналадок, необход для перехода от одной технологии к другой, получаем следующую математическую модель задачи: найти план интенсивностей использования технологийх = (x_i;... ;х_n),обеспеч-ий макс выпуска прод в стоим-ом выраж:∑a_ijx_j≤b_i (i=1,m)п ри огранич-ях на лимит-е ресурсы:maxZ= ∑c_jx_j и условии неотрицательности:x_j≥0 (j=1,n).

6.Задача о раскрое материалов. Суть задачи об опти­м-ом раскрое состоит в разраб-ке таких техн-ски допуст планов раскроя, при кот получ-ся необ­ход комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) свод к min-му. Рассмо­трим простейшую модель раскроя по одному измерению. Бо­лее сложные постановки ведут к задачам целочисл про­грамм-ия. Модель задачи раскроя по одному измер длинномер­ных материалов (прутков, труб, профильного проката и др.) может быть сформул так. Пусть имеется N штук ис­ходного материала, длина каждой штуки равна L. Нужны заготовки т видов, длины кот-х равны L_i(i = 1,n). Из­вестна потреб-сть в заготовках каждого вида, она равна b{. Изучение вопроса раскроя (построение технол-ой кар­ты раскроя) показ-ет, что можно выделить nприемлемых вариантов раскроя исход матер длиной Lна заго­товки длиной Zj. Обозначим через a_ijколичество заготовок i-го вида, получаемое при раскрое ед-цы исходного мате­риала по j-му (j=1,n) варианту, Cj — отходы при раскрое ед-цы исходн матер по j-му варианту. План задачи х = (х₁;... ; x_j ... ;х_n),где xj— кол-во ед-ц исходно­го материала, планируемое к раскрою по j-му варианту. Функция цели — min отходов, получ при рас­крое: minZ = ∑c_jx_j при огранич: на число ед исх матер: ∑x_j≤N

7.Формы записи задачи лп

Общ. задача ЛП:

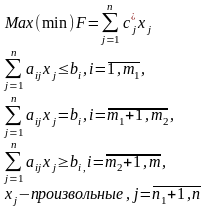
Симметр.ф.:

или

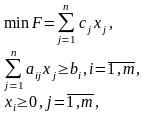
Канонич.ф.:

8.Переход к канон.Ф.:

Рассм.задачу:

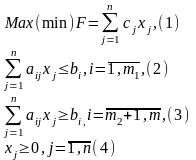
Преобраз.к канонич.виду.Введём m дополнит.неотриц.перемен: x_n+i≥ 0, i=1,m. Чтобы нер-во (2) преобраз. в р-во,к лев.ч. прибавим дополнит.переменные x_n+i≥ 0, i=1,m₁. Чтобы нер-во (3) преобраз.в р-во- вычтем доп.перемен. x_n+i≥ 0, i=m₁+1,m. Нер-ва примут вид:

Сист-у ур-ий (5)-(6) наз. эквивалентной сист-е (2)-(3) с усл. Неотриц-сти дополнит.перем-ых. Они в Цф вводятся с коэф-тами= 0, т.е. с_n+i=0. В рез-те получим задачу в канонич.форме:

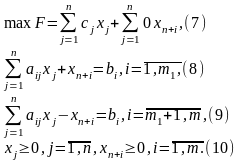
Теорема: Каждому допустим. реш-ию(x₁⁰, x₂⁰… x_n⁰) задачи (1)-(4) соотв. вполне определ. допуст-ое реш-е(x₁⁰, x₂⁰… x_n⁰, x_n+1⁰… x_n+m⁰)задачи (7)-(10) и наоборот,где , x_n+i⁰ ≥0, i=1,m.

Док-во: Пусть(x₁⁰, x₂⁰… x_n⁰)-допустимое решение задачи(1-4).(необходимо преобразовать 8 и 9-перенести знак суммы вправо и поставить знак >= 0, назвать их 11 и 12).

Из условий 11 и 12 следуют условия 8 и 9. Отсюда (x₁⁰, x₂⁰… x_n⁰, x_n+1⁰… x_n+m⁰) есть определенное допустимое реш-е задачи (7-10). Аналогично док-ся обратное утверждение.

9. Переход к сим-ной форме записи задачи, осущ-ся 2-мя спос-ми:

1сп. пусть к задаче ЛП имеются уравн-я рав-ва: 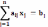. Каждое такое огранич-е рав-ва эквив-но в сис-ме нер-в: , 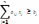. Нер-во вида «≥» умножением обеих частей на (-1) преобр-ся в нер-во «≤», и наоборот.

2сп. Рассм-м задачу в канон-м виде:

max(min) F=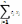 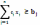, (1)

,i=1,m, (2)

x_j≥0, j=1,n (3).Преобр-м (2) к симметр-му виду. Нап-р, методом Гаусса, можно привести к виду: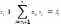 ,i=1,m (4)

пусть ранг системы (4) =m, m<n, тогда сис-ма имеет бескон-ное множ-во реш-й. Перем-ные x₁,x_2,…,x_m наз-ся БП, а перем-ныеx_m+1,x_m+2…x_n–СП, выразим ЦФ через СП, для этого подставим БП в ЦФmax(min) F= =

Испол-я данные обознач-я ЦФ можно записать в след-м виде: F= . Из сис-мы , i=1,m в силу того, что всеx_j≥0, j=1,n можем записать, что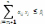 ,i=1,m. Т. oбр. получили симметр-ную форму записи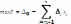 , ,i=1,m , x_j≥0, j=m+1,n.Отметим, что в любом случае при подстановке БП в ЦФ справедлива формула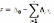 -это испол-ся для контроля выч-ий при реш задачи симп-ным мет-м. Если некот-е переем-е явл-ся отриц, то они замен-ся разностью 2-х полож-хx_k=x_k’-x_k’’, где x_k’≥0, x_k’’≥0

10.Геом. Интерпретация цф и ограничений задачи.

Рассм-м задачу с 2-мя перем-ми

max F=c₁x₁+c₂x₂ (1)

a_i1x₁+a_i2x₂ {≤,=,≥}b_i , i=1,m (2)

x_j≥0, j=1,n (3)

Дадим геом интерпретацию эл-тов этой задачи.

Каждое из огран-й 2-3 задаёт на плоскости х₁Ох₂ некот-ю полуплоскость. Пол-ть-выпуклое множ-во. Пересеч-е любого числа множ-в явл-ся выпуклым мн-вом (из этого след-т)ОДР 1-3 явл-ся выпуклое множ-во. Пусть сис-ма огран-й образ-т ОДР след-го вида (рисунок)

Выберем произвольное знач. F=F_0, получ c₁x₁+c₂x₂ = F₀ – урав-е прямой линии. В точках прямой (NM) ЦФ прин-т одно и тоже постоянное знач-е F_{0 ,} считая в (1) F-парам-м, получим уравн-е семейства парал-х прямых, кот-е наз-ся линиями уровня ЦФ. Для того, чтобы устан-ть направл-е возраст-я (убыв-я) ЦФ найдем её частные произ-ные по неизвестным парам-м .Вектор наз-ся градиентом и указ. напрвл-е наискор-го возраст-я ЦФ векторназ-ся антиград-м и указ-т напр-ние наискор-го убыв-я ЦФ. Векторы перпенд-на прямым F=const семейства c₁x₁+c₂x₂ = F_.

11. Рассмзад-чу с 2-мя переменнымиmaxF=c₁x₁₊c₂x₂

a_11x1+ a₁₂x₂{≤,≥,=}b₁

_{…………..}

a_m1x₁₊a_m2x₂{≤,≥,=}b_m, ,

x₁≥0,x₂≥0

Каждое из огранич,задает на плоскости x₁ox₂нект-ую плоскость. Полуплоскость явл. выпуклмнож-ом. Пересеч люб. числа выпуклых мно-в явл. вып. мно-вом,отсюда следует ОДР задачи явл.выпуклое мн-во.С₁x₁₊ c₂x₂=F₀ – ур-е прямой линии.В точках прямой NM ЦФ прин одно и то же пост значF₀,считая параметром получур-е семейства параллпрямых,к-е наз-ся линиями уровня ЦФ.Длятого,чтобыустаноитьнаправлвозр(убыв) ЦФ найдем ее частные произв-ые по неизвестным параметрам.Вектор С=(С₁,С₂) наз-ся град-м и ук-етнаправ-е наискор-говозр ЦФ. Вектор –С=(-С₁,С₂₎ – антиградиент и указывает убывание ЦФ.Граф.метод решения:1.С учетом сис-мы ограничений строим ОДР;2.строим вектор градиент;3.провод. прямуюF=F₀,перпенд.вектору градиенту в начале координат;4.решая задачу наmax,перемещ прямуюF=0 так, чтобы она касалась ОДР в ее крайней точке, если на minF=0 – линию;5.определяем оптим-й план Х* и экстремальноезнач-е ЦФ F*.