Гипотеза о значении среднего для одной выборки

Периодически возникающей проблемой маркетинговых исследований является необходимость делать определенные предположения о среднем значении генеральной совокупности. Отметим, что когда берутся выборки из какой-то генеральной совокупности с известной дисперсией, то распределение выборочных средних совпадает с распределением генерального среднего, а разброс выборочных средних равен разбросу генерального среднего, поделенному на объем выборки, т. е. . Таким образом, нет ничего удивительного в том, что когда разброс генеральной совокупности известен, подходящей статистикой проверки гипотезы о среднем оказывается:

где — выборочное среднее; — среднее генеральной совокупности; — стандартная ошибка среднего, которая равна , где п — объем выборки, а — стандартное отклонение для генеральной совокупности.

Статистика z приемлема, если выборка берется из нормальной генеральной совокупности, или если переменная распределена в генеральной совокупности не по нормальному закону, но выборка достаточно велика для того, чтобы подпадать под действие центральной предельной теоремы. И все же, что происходит в наиболее реальном случае, когда разброс для генеральной совокупности неизвестен?

Когда разброс генеральной совокупности неизвестен, конечно, неизвестна и стандартная ошибка среднего , поскольку она равна . Стандартная ошибка среднего должна в таком случае оцениваться по выборочным данным. Эта оценка , где — несмещенное выборочное стандартное отклонение, определяемое как:

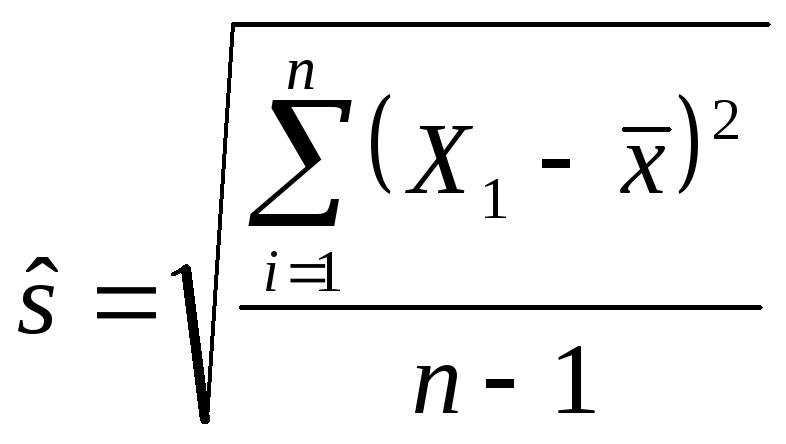
Или, другими словами,

Теперь тестовой статистикой становится

или величина которая подчиняется t-распределению с n-1 степенями свободы, если удовлетворяются условия t-проверки.

Чтобы приемлемым образом использовать t-статистику для предположений о среднем, необходимо ответить на два базисных вопроса.

• Является ли распределение переменной в генеральной совокупности нормальным или оно асимметрично?

• Велик или мал объем выборки?

Если интересующая переменная распределена в генеральной совокупности нормально, то статистика проверки имеет t-распределение с п-1 степенями свободы. Это верно вне зависимости от того, велик или мал объем выборки. Обычно мы используем t-распределение с n-1 степенями свободы, делая предположение для малых выборок. Хотя теоретически принимать t-распределение с п-1 степенями свободы также корректно и для больших значений п, это распределение приближается к нормальному и становится от него неотличимым, когда объем выборки достигает 30 или более наблюдений. По этой причине при относительно больших выборках со статистикой проверки следует обращаться к таблице нормальных отклонений. Тем не менее, следует подчеркнуть, что в основе этого лежит то обстоятельство, что теоретически корректное t-распределение (при неизвестном у) становится неотличимым от нормального распределения.

Что происходит, когда при неизвестном у переменная не распределена в генеральной совокупности нормально? Если распределение переменной симметрично, либо показывает лишь умеренную скошенность или асимметрию, то никакой проблемы нет. Принятие нормального распределения в качестве отправного предположения для t-распределения вполне надежно. Однако если в генеральной совокупности переменная обладает высокой скошенностью, подходящий метод зависит от размера выборки. Когда выборка мала, t-проверка неприемлема. Либо переменная должна быть преобразована таким образом, чтобы ее распределение стало нормальным, либо придется использовать одну из статистических проверок свободного распределения. Когда выборка велика, для принятия предположения должна использоваться нормальная кривая. При этом необходимо удовлетворение двух следующих допущений:

1. Объем выборки достаточно велик, чтобы выборочное среднее было распределено нормально в соответствии с центральной предельной теоремой. Чем выше степень асимметрии, тем больший объем выборки необходим для удовлетворения этого допущения.

2. Выборочное стандартное отклонение является близкой оценкой стандартного отклонения генеральной совокупности. Чем выше степень разброса генеральной совокупности, тем больший объем выборки необходим для подтверждения этого допущения.

В Исследовательском окне 20.1 дается итоговый обзор ситуации принятия предположений о среднем при известном и неизвестном стандартном отклонении у генеральной совокупности и нормальном либо асимметричном распределении генеральной совокупности.

Исследовательское окно 20.1

Проверка гипотез об одном среднем

	известно	неизвестно
Распределение переменной в генеральной совокупности нормальное или симметричное	Малое п: Используется	Малое п: Используется где и И обращение к t-таблице для n-1 степеней свободы.
	Большое п: Используется	Большое п: Поскольку t-распределение приближается к нормальному с возрастанием п, используется для n>30
Распределение переменной в генеральной совокупности асимметрично	Малое п: Теоретической поддержки параметрической проверки не существует. Либо необходимо преобразовать переменную таким образом, чтобы она была распределена нормально, а затем использовать г-проверку, либо прибегнуть к статистической проверке свободного распределения.	Малое п: Теоретической поддержки параметрической проверки не существует. Либо необходимо преобразовать переменную таким образом, чтобы она была распределена нормально, а затем использовать t-проверку, либо прибегнуть к статистической проверке свободного распределения.
	Большое п: Если выборка достаточно велика, чтобы действовала центральная предельная теорема, используется	Большое п: Если выборка достаточно велика, чтобы (1) действовала центральная предельная теорема и (2) являлась близкой оценкой , используется

Чтобы проиллюстрировать применение t-проверки, рассмотрим сеть супермаркетов, которая исследует желательность добавления какого-то нового товара к тому, что уже есть на полках ее магазинов. Поскольку многие товары должны конкурировать между собой за обладание ограниченным пространством полок, запасы определялись исходя из того, что недельная продажа в каждом магазине 100 единиц данной позиции ассортимента является достаточной гарантией прибыльности. Предположим, что исследовательский отдел решил изучить оборот по рассматриваемой позиции, представив данные в виде случайной выборки по десяти магазинам за какой-то ограниченный период времени. Предположим далее, что средний недельный объем продаж одного магазина оказался таким, как представлено в табл.20.2.

Поскольку разброс объема продаж одним магазином неизвестен и должен оцениваться, t-проверка является корректной параметрической проверкой, если распределение продаж подчиняется нормальному закону. Предположение о нормальности распределения представляется разумным и может быть проверено с использованием одного из критериев согласия. Малый объем продаж не указывает на какую-то реально существующую асимметрию, поэтому предположим, что допущение о нормальности распределения удовлетворяется.

Приемлема однонаправленная проверка, поскольку, только когда объем продаж одного магазина в неделю составит, по крайней мере, 100 единиц, этот товар будет выведен на рынок в национальном масштабе. Нулевой и альтернативной гипотезами являются

а предполагаемый уровень значимости должен быть =0,5. По данным табл. 20.2

Или

или

и поэтому оценочная стандартная ошибка среднего есть . Расчеты дают

Критическое t, определяемое по t-таблице при =п-1=9 степенях свободы, составляет 1,833 (р=0,95). (См. табл. 3 приложения в конце книги.) Поэтому вряд ли рассчитанное значение могло бы возникнуть случайно, если бы объем продаж на один магазин в генеральной совокупности был действительно меньше или равен 100 единицам в неделю.

Прогноз ожидаемых недельных продаж одного магазина при условии вывода товара на рынок в национальном масштабе можно получить, рассчитав доверительный интервал. Подходящая для этого формула выглядит следующим образом:

или

Как мы уже видели, для 95% доверительного интервала и 9 степеней свободы t=1,833. Таким образом, 95% доверительный интервал составляет 109,4±(1,833)(4,55) или 109,4±8,3, либо в ином представлении

101,1==117,7.

Предположим, что товар размещается для продажи в 50 магазинах, и что выборочное среднее и выборочное стандартное отклонение остаются теми же самыми, т. е. =109,4 и = 14,4. Статистика проверки будет теперь z=4,62, что соответствует таблице нормального распределения, поскольку для выборок такого объема I неотличимо от нормального распределения. Расчетное значение z больше критического z=1,645 для =0,05, и, как и ожидалось, мы пришли к тому же выводу. Теперь обоснование даже сильнее, так как выборка магазинов больше; можно ожидать, что товар будет продаваться интенсивнее, чем 100 единиц в неделю в каждом магазине.

Влияние более солидной выборки и возможности использовать в этих обстоятельствах нормальную кривую можно также обнаружить по тому, что чем меньше доверительный интервал, тем более солидной получается выборка. Когда применяется нормальная кривая, а не кривая t-распределения, формула для расчета доверительного интервала меняется на , где соответствующее значение z берется из таблицы нормальной кривой. Поскольку для 95% доверительного интервала z=1,645, он оказывается равным 109,4±(1,645)(4,55) или 109,4±7,5, что дает оценку , т. е. несколько более узкий интервал для 50 магазинов в выборке, чем в случае выборки из 10 магазинов.