Глава двадцатая. Анализ данных: оценка различий

В процессе анализа данных исследования регулярно возникает вопрос: Достаточно ли статистически значимы результаты исследования? Не могли результат получиться именно таковым по тон причине, что имел место контакт только с ограниченной выборкой, или он действительно показывает фундаментальное состояние популяции в целом? Для ответа на этот вопрос мы используем одну из проверок статистической значимости. В настоящей главе дается обзор некоторых наиболее важных проверок статистической значимости различий. Рассматриваемое различие может быть разностью результата для определенной выборки и некоторым ожидаемым значением для генеральной совокупности в целом, так и разностью между результатами, полученными на двух и более выборках. Для разных типов проблем применяются разные виды проверок. В первой части главы рассматривается проверка состоятельности по критерию (хи-квадрат), которая особенно полезна при нормальном распределении данных. Во второй части уделено внимание критерию Колмогорова-Смирнова, который применяется при анализе дискретных (упорядоченных) распределений данных. В последних разделах обсуждение сосредоточено на критериях, которые применимы, когда анализируемые разности представляются средними или долями.

Проверка согласия

В маркетинговых исследованиях часто возникает ситуация, когда аналитик должен определить, соответствует ли определенный образец поведения, о котором свидетельствуют данные, тому образцу, который ожидалось обнаружить, когда исследование задумывалось. В качестве иллюстрации рассмотрим поставщика готовых завтраков, который недавно разработал рецепт новой каши, названной Score. Каша поставлялась в трех размеров стандартных упаковках: малом, большом и семейном. В прошлом этот поставщик установил, что на каждую одну проданную упаковку малого размера продавалось три большого и две семейного размеров. Ему захотелось посмотреть, сохраняется ли та же тенденция для новой каши, поскольку изменение образцов потребления могло существенно отразиться на производстве. По этой причине наш производитель каши решил провести рыночный тест для определения относительных частот приобретения покупателями новой каши в разных упаковках.

Предположим, что в процессе надлежащим образом организованного рыночного теста недельной продолжительности было продано 1200 коробок новой каши, и что распределение этого объема продаж по размерам коробок выглядело следующим образом:

Количество покупок
Малых 240	Больших 575	Семейных 385	Всего 1200

Несложным перемножением можно показать, что эти цифры не соответствуют образцу соотношения, установленного по другим маркам каши для завтраков. Является ли это свидетельством того, что фирма должна ожидать изменения образцов спроса на Score в упаковках различного размера?

ПРОВЕРКА СОГЛАСИЯ ПО КРИТЕРИЮ ХИ-КВАДРАТ

Статистическая проверка, проводимая для определения, соответствует ли какой-то наблюдавшийся образец частот распределению гипотетической генеральной совокупности.

Для решения этого типа задач хорошо подходит проверка согласия по критерию хи-квадрат.

(Заметим, что хи — название буквы греческого алфавита). Множество значений, принимаемых интересующей нас переменной, разбивается на k взаимоисключающих интервалов (в примере k=3). Каждое наблюдение логически попадает в один из этих интервалов. Предполагается, что испытания независимы и объем выборки велик.

Все, что необходимо для проведения проверки, это определить значения вероятностей попадания в рассматриваемые интервалы для значений из гипотетической генеральной совокупности (т. н. ожидаемое число событий) и сравнить их с числом значений из выборки действительно попавших в соответствующие интервалы (наблюдавшимся числом событий), используя уравнение:

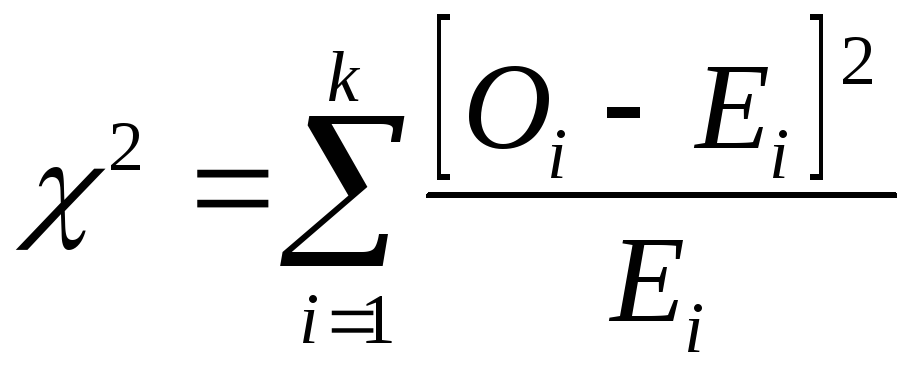
где: — наблюдавшееся число событий, попадающих в i-й интервал; — ожидаемое число событий, попадающих в i-и интервал; k — количество интервалов.

Ожидаемое число по интервалам (категориям) получается из нулевой гипотезы, которая в рассматриваемом примере состоит в том, что состав продаж Score, отличающихся размерами упаковки, будет повторять нормальное для изготовителя соотношение (т. е. на продажу каждой малой упаковки будет приходиться продажа трех упаковок большого размера и двух семейного размера). В терминах долей всех продаж это будет означать

малый размер:

большой размер:

семейный размер:

или, что следует ожидать, одной шестой продаж новой каши в упаковке малого размера, половины в упаковке большого размера и одной трети в упаковке семейного размера, если продажа новой каши следует традиционным образцам потребления. Если продажа 1200 коробок во время тестирования рынка подчинялась нормальному или ожидаемому образчику потребления 200(1/6х1200), то должно быть малого размера, 600(1/2х1200) должно быть большого размера и 400(1/3х1200) должно быть семейного размера. Каким образом наблюдавшийся образец сравнивается с ожидаемым образцом наблюдения? Рассчитывается соответствующая статистика следующим образом:

Распределение хи-квадрат представляет собой одно из статистических распределений, определяемое величиной, называемой степенью свободы . Под термином степени свободы подразумевается такое количество параметров, характеризующих состояние некоторого объекта, которые могут меняться независимо. Например, если у вас есть пять чисел, для которых вы рассчитали среднее, то, зная любые четыре числа и среднее, вы в состоянии определить пятое число. Степени свободы в проверке по хи-квадрат определяются тем, насколько много ячеек таблицы могут произвольно варьироваться. Например, у нас есть следующая таблица:

	В1	В2
A1	1	4*	5
A2	3*	4*	7
	4	8

и задано одно из значении ее ячеек, скажем, левое верхнее значение.

	В1	В2
A1	x	x	5
A2	x	x	7
	4	8

Тогда оказываются зафиксированными все значения со звездочками, потому что нам были заданы итоги по столбцам и строкам таблицы. Если мы знаем, что A₁ В₁=1, то автоматически определяется каждое из остальных значений. Исходя из этого, мы говорим, что свободна для варьирования только одна ячейка.

В примере с кашей число степеней свободы на единицу меньше числа категорий (k), т. е. =k-1 = 2, поскольку сумма разностей между наблюдаемыми и ожидаемыми частотами есть ноль; и ожидаемая и наблюдаемая частоты должны давать в сумме полное число событий; при задании любых k-1 разностей остающаяся разность оказывается, таким образом, зафиксированной, что и приводит к потере одной степени свободы.

Пусть для этой проверки исследователь выбрал уровень значимости =0,05.Табулированное значение для двух степеней свободы и =0,05 составляет 5,99 (см. табл. 2 приложения в конце книги). Поскольку рассчитанное значение (=9,60) больше, заключение состоит в том, что выборочный результат вряд ли является всего лишь случайным. Скорее, результаты предварительного рыночного тестирования показывают, что продажа Score будет идти иным образом, чем считалось типичным для данной продукции. Нулевая гипотеза о продаже в соотношении 1:3:2 отвергается.

Описанная здесь в общих чертах проверка по хи-квадрат является приблизительной. Приближение оказывается сравнительно неплохим, если, как общее правило, ожидаемое число событий в каждой категории равно пяти или более, хотя в некоторых ситуациях это значение может опускаться даже до 1.

Еще одно использование проверки согласия по хи-квадрат заключается в определении того, имеет ли распределение генеральной совокупности какую-то конкретную форму. Например, мы можем быть заинтересованы в обнаружении того, может ли выборочное распределение оценок возникать из их нормального распределения. Чтобы осуществить такое исследование, мы должны построить гистограмму выборочных частот. Интервалы должны соответствовать k ячейкам, по которым проверяется согласие. Наблюдавшиеся частоты по ячейкам должны представлять собой число наблюдений, попадающих в каждый интервал. Ожидаемые частоты по ячейкам будут числами, попадающими в каждый интервал, если выборка в самом деле взята из нормального распределения со средним и дисперсией . Если среднее и дисперсия для генеральной совокупности были неизвестны, то в качестве оценок должны использоваться соответствующие статистики выборки и ее разброса. Это приведет к дополнительной потере двух степеней свободы, но базисная процедура проверки останется неизменной.